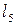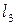- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Неорієнтовані графи
Визначення 2.1. Граф — це сукупність непорожньої множини (точок) V і множини (ліній) Е, між якими визначено відношення відповідності (інцидентності) &, причому кожний елемент  відповідає двом елементам
відповідає двом елементам  ,
,  .
.
Елементи множини V називають вершинами графа G і позначають великими буквами А, В, С…, або цифрами 1, 2, … . Відповідно елементи множини Е називають ребрами і позначають (А; В), (А; С),…, (1; 2), (1; 3),… ,.
Графи, в яких множини Е і V — скінченні (порожня множина також розглядається як скінченна), називаються скінченними.
Зауважимо, що множина Е (але не V) може бути порожньою. Кажуть, що граф вироджений тоді і тільки тоді, коли він не має ребер.
Вершини, які не належать жодному ребру, називаються ізольованими. Отже, в виродженому графі всі вершини ізольовані.
Вершини  і
і  , які відповідають (інцидентні) ребру
, які відповідають (інцидентні) ребру 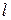 , називають його граничними точками. Інколи кажуть, що вони з’єднуються ребром
, називають його граничними точками. Інколи кажуть, що вони з’єднуються ребром 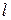 і позначають
і позначають  . Якщо
. Якщо  , то
, то 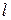 називається петлею.
називається петлею.
Під паралельними розуміють ребра 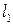 i
i  , для яких
, для яких  і
і  . Зокрема, дві петлі, інцидентні одній і тій вершині, є паралельними.
. Зокрема, дві петлі, інцидентні одній і тій вершині, є паралельними.
Кажуть, що вершини  і
і  суміжні, якщо існує хоча б одне ребро
суміжні, якщо існує хоча б одне ребро 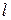 таке, що
таке, що  . Зокрема, вершина
. Зокрема, вершина 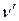 суміжна сама з собою, якщо існує петля, інцидентна
суміжна сама з собою, якщо існує петля, інцидентна 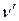 ; в протилежному випадку
; в протилежному випадку 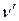 не може бути суміжна сама з собою. Аналогічно ребра
не може бути суміжна сама з собою. Аналогічно ребра 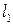 і
і  називають суміжними, якщо вони мають, по крайній мірі, одну спільну граничну точку.
називають суміжними, якщо вони мають, по крайній мірі, одну спільну граничну точку.
Зауважимо, що суміжність є відношенням між двома подібними елементами (між вершинами, або між ребрами), тоді як інцидентність є відношення між різнорідними елементами.
Визначення 2.2. Число ребер, інцидентних вершині 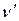 (петля враховується двічі), називається степенем вершини
(петля враховується двічі), називається степенем вершини 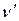 і позначається
і позначається  .
.
Отже, вершина 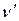 — ізольована, якщо
— ізольована, якщо  . Зокрема, для всіх вершин
. Зокрема, для всіх вершин  виродженого графа
виродженого графа  .
.
Наголосимо на деякі властивості графів, пов'язані з поняттям степеня вершини:
а) в графі G сума степенів всіх його вершин — число парне і в два рази більше від числа його ребер;
б) число непарних вершин будь-якого графа — парне;
в) в будь-якому графі з n вершинами, де  , завжди знайдуться хоча б дві вершини з однаковими степенями;
, завжди знайдуться хоча б дві вершини з однаковими степенями;
г) якщо в графі з n вершинами ( 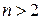 ) дві вершини мають однаковий степінь, то в цьому графі завжди знайдеться або одна вершина степеня 0, або одна вершина степеня (
) дві вершини мають однаковий степінь, то в цьому графі завжди знайдеться або одна вершина степеня 0, або одна вершина степеня ( 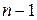 ).
).
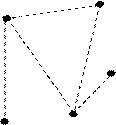
Проілюструємо сказане вище на графі, який зображений на рис.2.1.
 |
|
|
|
|
|
Рис. 2.1.
Граничними точками ребра  є вершини
є вершини 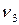 і
і  . Петля
. Петля 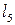 має єдину граничну точку
має єдину граничну точку  . Ребро
. Ребро  суміжне з ребром
суміжне з ребром 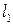 і паралельне ребру
і паралельне ребру 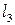 . Вершина
. Вершина  суміжна з
суміжна з 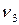 і сама з собою. Вершини
і сама з собою. Вершини 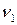 ,
, 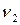 ,
, 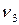 ,
,  мають парний степінь, а вершина
мають парний степінь, а вершина 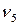 є ізольованою і її степінь дорівнює нулю.
є ізольованою і її степінь дорівнює нулю.
Визначення 2.3. Скінченна послідовність ребер графа 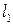 ,
,  ,…,
,…,  (не обов’язково різних) називається маршрутом довжини n, якщо існує послідовність
(не обов’язково різних) називається маршрутом довжини n, якщо існує послідовність 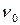 ,
, 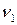 ,
, 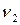 ,…,
,…,  , з
, з  (не обов’язково різних) вершин таких, що
(не обов’язково різних) вершин таких, що  ,
, 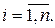
Кажуть, що маршрут замкнутий, якщо  і незамкнутий, якщо
і незамкнутий, якщо 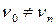 . В останньому випадку також кажуть, що маршрут з’єднує вершини
. В останньому випадку також кажуть, що маршрут з’єднує вершини 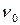 і
і  . Зауважимо, що одне ребро можна розглядати як маршрут довжиною 1.
. Зауважимо, що одне ребро можна розглядати як маршрут довжиною 1.
Якщо всі ребра маршруту різні, а сам маршрут незамкнутий, то його називають ланцюгом і – циклом, якщо він замкнутий.
Якщо всі  вершини
вершини 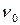 ,
, 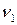 ,
, 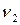 ,…,
,…,  — різні (очевидно, що в цьому випадку ребра різні), то відповідний ланцюг називається простим ланцюгом.
— різні (очевидно, що в цьому випадку ребра різні), то відповідний ланцюг називається простим ланцюгом.
Якщо  , а всі решта вершини різні, то послідовність ребер називається простим циклом.
, а всі решта вершини різні, то послідовність ребер називається простим циклом.
Зауважимо, що якщо у графах всі прості цикли парної довжини, то граф не має жодного циклу непарної довжини.
Інколи в літературі ланцюг (простий ланцюг) називають ще шляхом (простим шляхом).
Граф G називається повним, якщо кожні дві різні вершини з’єднані одним і тільки одним ребром.
В повному графі кожна його вершина належить одному і тому числу ребер. Тому для його задання достатньо знайти число його вершин. Таким чином, степінь кожної вершини графа на одиницю менший від числа його вершин.
Граф, який не є повним, можна перетворити в повний, провівши потрібні ребра. Вершини графа G разом з доповненими ребрами також утворюють граф, який називається доповненням графа G і позначається  .
.
Граф G і його доповнення  зображені на рис.2.2.
зображені на рис.2.2.
 | |||||
 | |||||
 |
| G | 
|
Рис. 2.2.
Число ребер повного графа дорівнює  .
.
Визначення 2.4. Граф G називається зв’язним, якщо кожна пара різних вершин може бути з’єднана, по крайній мірі, одним ланцюгом.
В іншому випадку граф називається незв’язним.
Визначення 2.5. Граф називається деревом, якщо він зв’язний і не має циклів.
Визначення 2.6. Граф, який не має циклів і складається з k дерев, називається лісом з k дерев.
Граф є деревом тоді і тільки тоді, коли кожна пара різних вершин з’єднується одним і тільки одним ланцюгом.
Видалення будь-якого ребра з дерева робить його незв’язним. З другої сторони, з будь-якого зв’язного графа, який не є деревом, можна видалити деякі ребра, не порушуючи зв’язності (наприклад, будь-яке ребро, яке входить в цикл).
Під підграфом 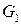 графа G розуміють граф, який складається з частини ребер і вершин G, для яких зберігається відношення інцидентності, що має місце в графі G при умові, що множина вершин підграфа G повинна включати всі граничні точки множини його ребер. Граф G називають ще надграфом графа
графа G розуміють граф, який складається з частини ребер і вершин G, для яких зберігається відношення інцидентності, що має місце в графі G при умові, що множина вершин підграфа G повинна включати всі граничні точки множини його ребер. Граф G називають ще надграфом графа 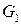 .
.
Відповідно дерево Т можна означити, як мінімальний зв’язний граф, де мінімальність означає, що він не містить підграфу, який складається зі всіх його вершин і є зв’язним.
Якщо дерево Т є підграфом графа G, то ребра G, які належать дереву Т, називають вітками дерева Т, а ребра, які не належать дереву Т — хордами відносно дерева Т.
Визначення 2.8. Ребро (А; В) графа G називається мостом, якщо в графі  , що отримали з графа G в результаті видалення ребра (А, В) вершини А і В будуть незв’язними.
, що отримали з графа G в результаті видалення ребра (А, В) вершини А і В будуть незв’язними.
Таким чином, кожне ребро в дереві (лісі) є мостом.
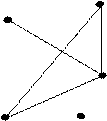
Про граф, всі вершини якого належать дереву Т, кажуть, що дерево Т покриває граф G. Очевидно, що тільки зв’язні графи мають покриваючі дерева.

Рис. 2.3.
Дерева  і
і 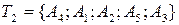 – два різні покриваючі дерева для одного і того ж графа G. Той факт, що кожне з дерев
– два різні покриваючі дерева для одного і того ж графа G. Той факт, що кожне з дерев  і
і 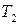 має по 4 ребра є наслідком загальної властивості дерев: кожне дерево з n вершинами має
має по 4 ребра є наслідком загальної властивості дерев: кожне дерево з n вершинами має  ребер; ліс із k дерев, який містить
ребер; ліс із k дерев, який містить  вершин має
вершин має 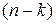 ребер.
ребер.
 Будь-які два дерева, які покривають один і той же граф, можна перетворити одне в одне, будуючи послідовність покриваючих дерев, кожне з яких відрізняється від попереднього одним ребром (рис. 2.4).
Будь-які два дерева, які покривають один і той же граф, можна перетворити одне в одне, будуючи послідовність покриваючих дерев, кожне з яких відрізняється від попереднього одним ребром (рис. 2.4).
Рис.2.4.
Читайте також:
- Henri Matisse- Биография художника на английском.
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Биография населенного мира
- Грамматико-орфографическая пропедевтика в период обучения грамоте.
- ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ
- Двочасткові графи
- ДЕМОГРАФИЯ
- Дифтонги i диграфи
- Дробот В. Изучение биографии писателя в школе.- К., 1988.
| <== попередня сторінка | | | наступна сторінка ==> |
| РОЗДІЛ 2. ГРАФИ І МЕРЕЖІ | | | Орієнтовані графи |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |