• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Математична індукція

Принцип математичної індукції:

Нехай — така множина, що

1. ;

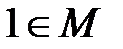2.

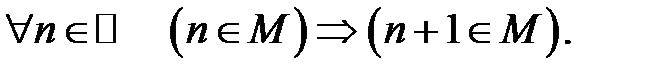
Тоді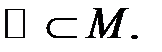

Цей принцип є аксіомою натуральних чисел, а також основою методу математичної індукції.

Метод математичної індукції:

1. Перевіряємо, що деяке твердження справджується для початкового номеру (база індукції).

2. Припускаємо, що це твердження вірне або для деякого номера 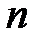, або для всіх натуральних чисел, починаючи з 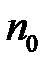, які не перевищують 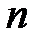(припущення індукції).

3. Аналізуючи припущення індукції, доводимо, що наше твердження вірне й для наступного номера 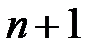(індукційний крок).

4. Робимо висновок, що дане твердження вірне для всіх натуральних чисел, починаючи з .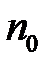

Приклад 1. Методом математичної індукції довести, що для всіх натуральних чисел має місце рівність

Доведення.

1. Рівність вірна при 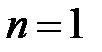. Дійсно,

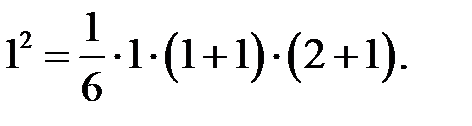
2. Припустимо, що рівність виконується для деякого натурального .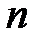

3. Доведемо рівність для 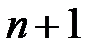, тобто

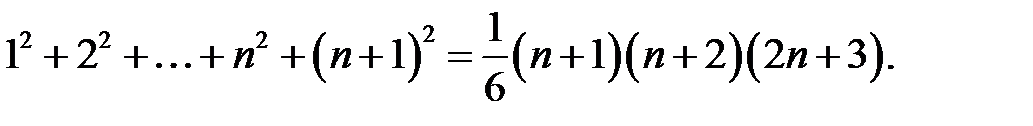
Дійсно,

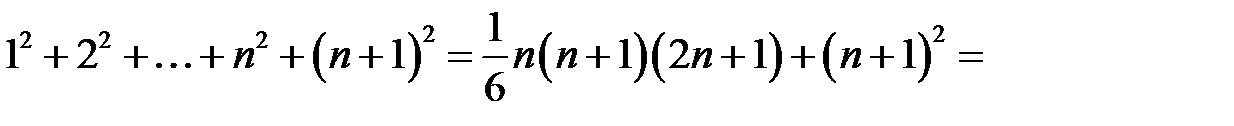
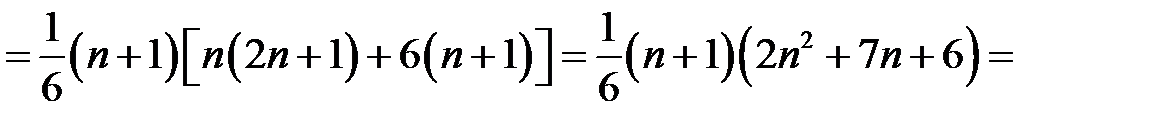
Згідно з принципом математичної індукції рівність виконується для всіх натуральних чисел.

Приклад 2. Довести методом математичної індукції, що число 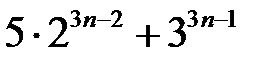ділиться на 19 для будь-якого .

Доведення.

1. Твердженя вірне при 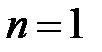. Дійсно,

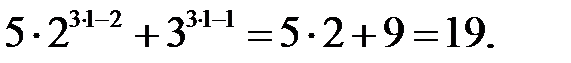
2. Припустимо, що твердження виконується для деякого натурального .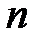

3. Доведемо твердження для 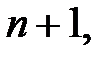тобто перевіримо, що вираз 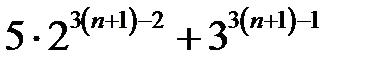ділиться на 19. Дійсно,

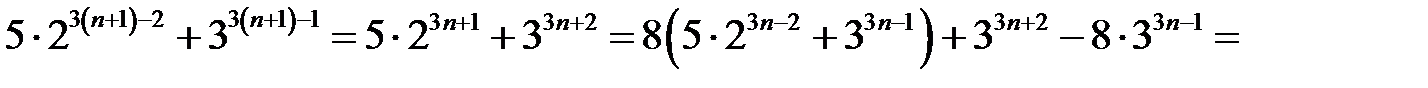
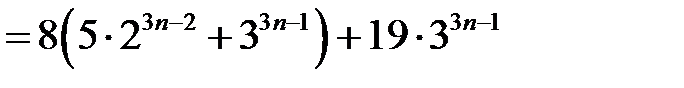
Перший доданок ділиться на 19 за припущеннням, другий доданок теж ділиться на 19. Отже твердження має місце для .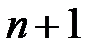

За принципом математичної індукції твердження виконується для всіх натуральних чисел.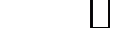

Приклад 3 (нерівність Бернуллі). Довести, що при 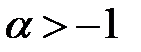та довільному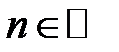

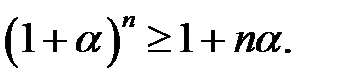
Доведення.

1. Нерівність справджується при 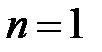. Дійсно,

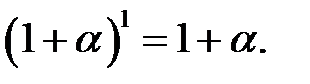
2. Припустимо, що нерівність виконується для деякого натурального .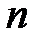

3. Доведемо нерівність для 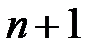, тобто

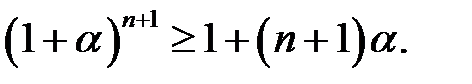
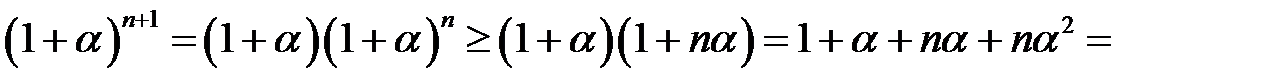
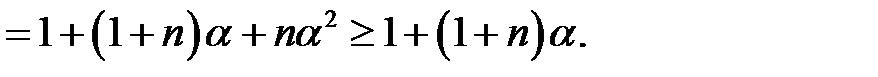
Таким чином, нерівність доведена для всіх натуральних чисел.

Завдання 1

Довести методом математичної індукції рівності:

1.

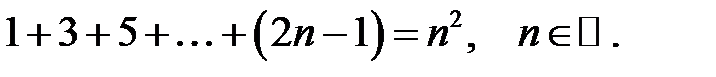
2.

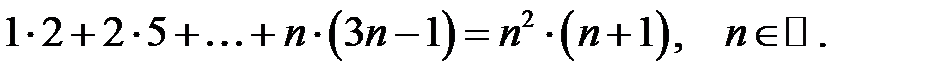
3.

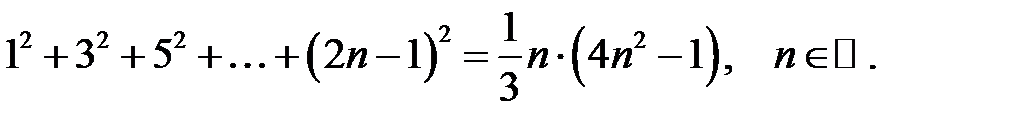
4.

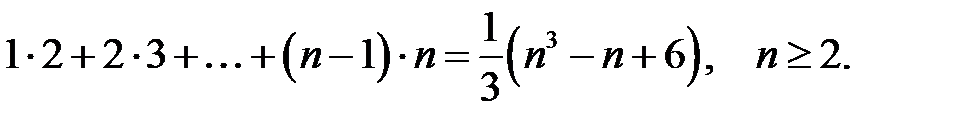
5.

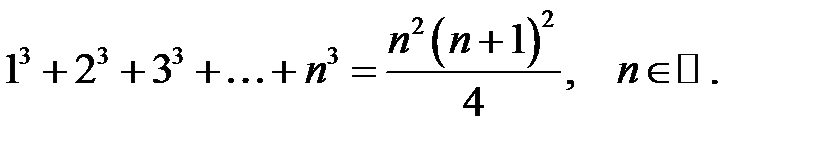
6.

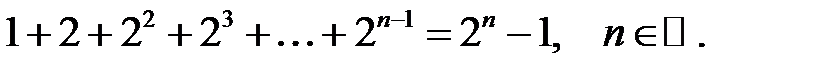
7.

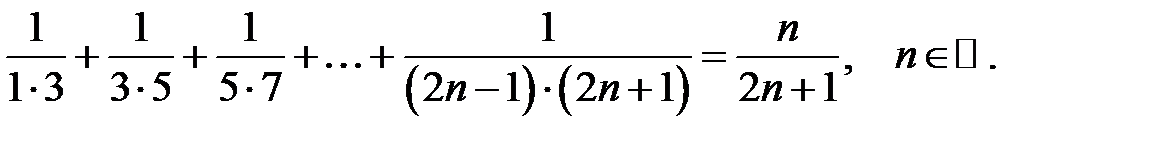
8.

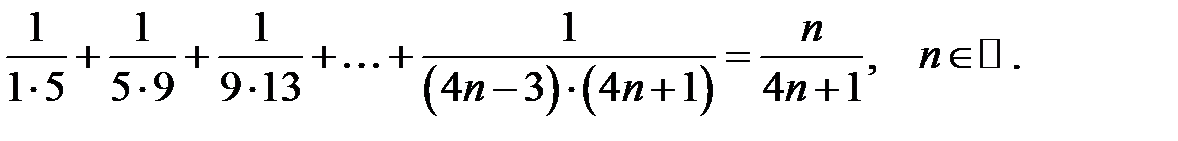
9.

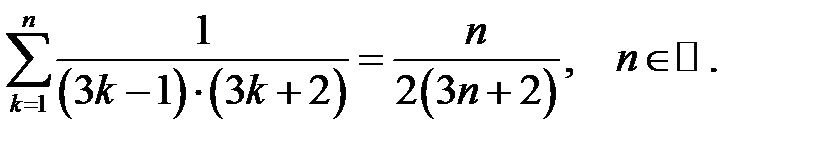
10.

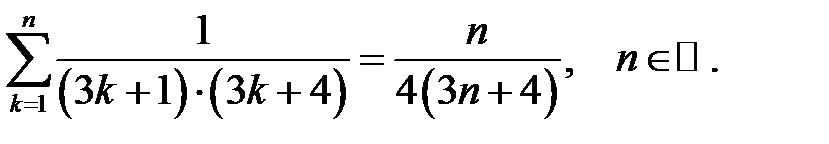
11.

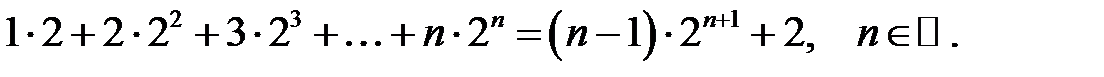
12.

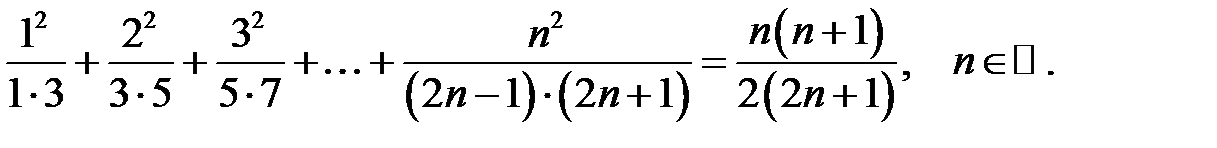
13.

14.

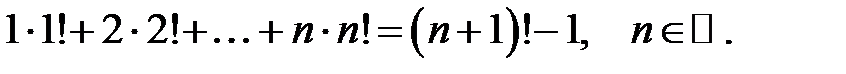
15.

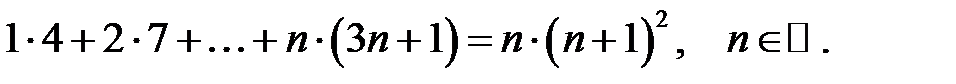
16.

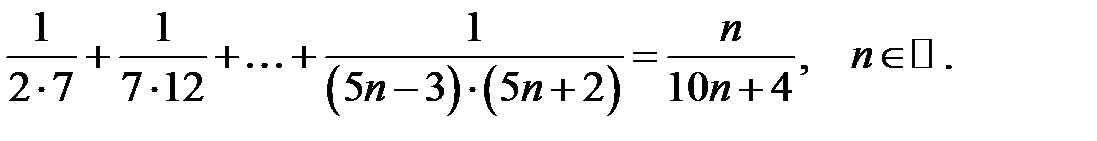
17.

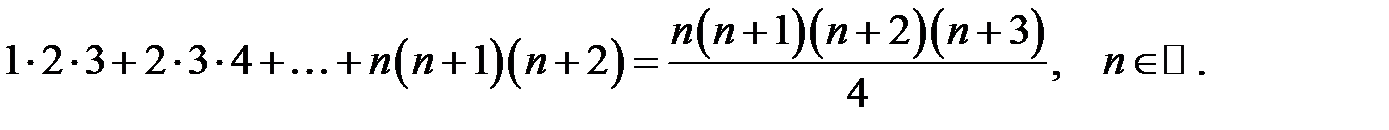
18.

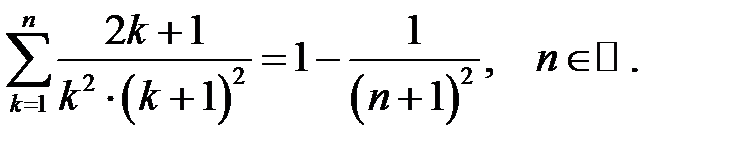
19.

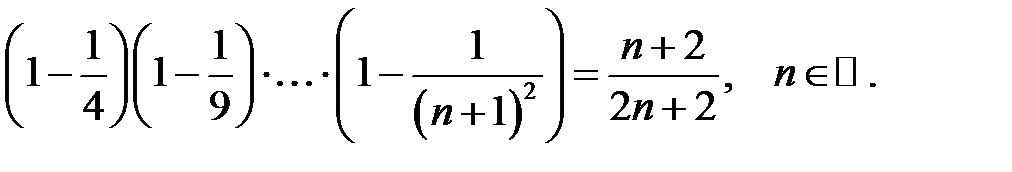
20.

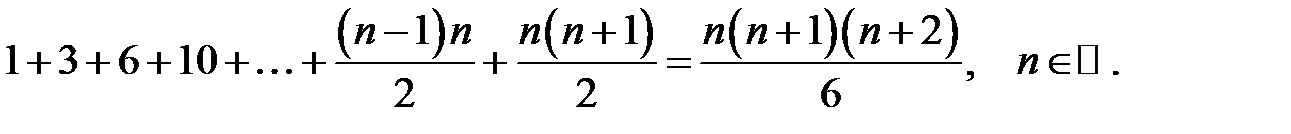
21.

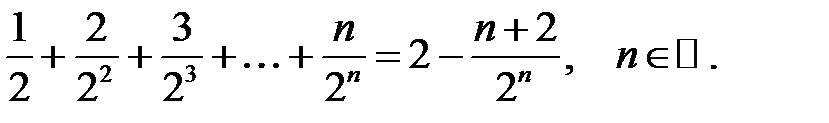
22.

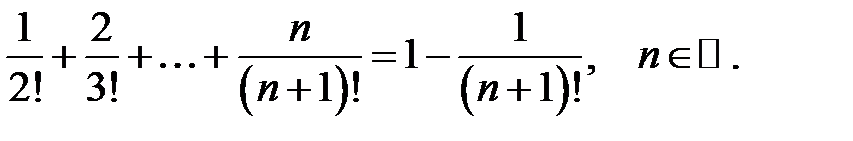
23.

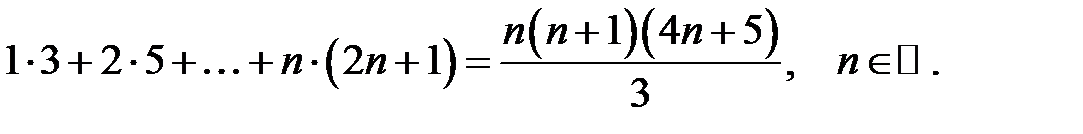
24.

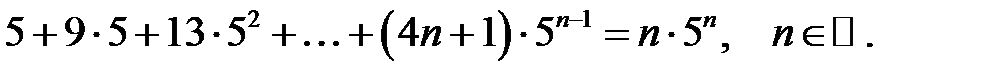
25.

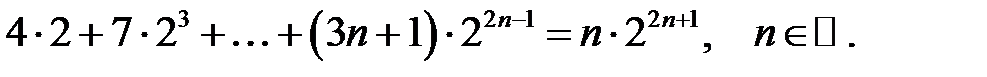
26.

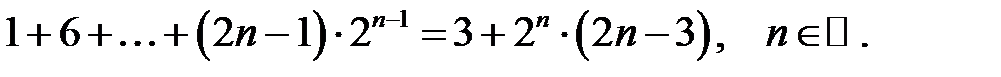
27.

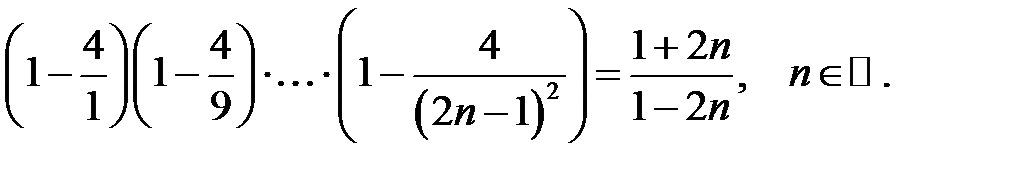
28.

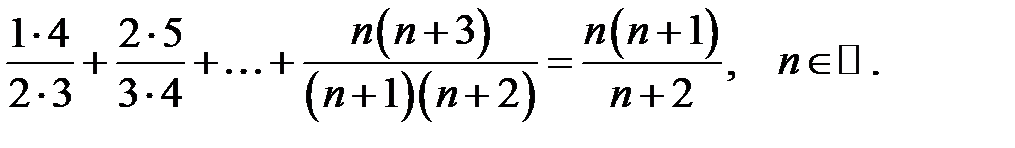
29.

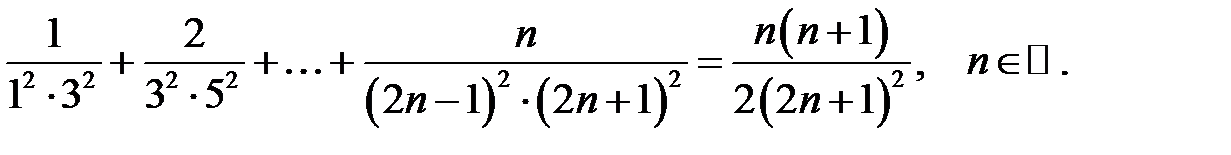
30.

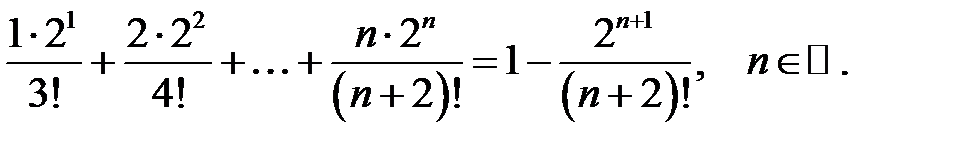
Завдання 2

Довести методом математичної індукції, що для всіх натуральних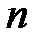

1. 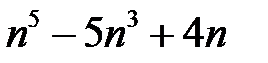ділиться на .

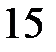2. 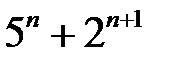ділиться на .

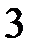3. 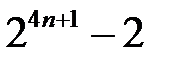ділиться на .

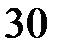4. 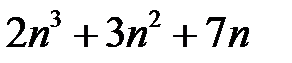ділиться на .

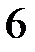5. ділиться на .

6. 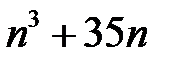ділиться на .

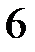7. 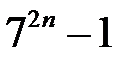ділиться на .

8. 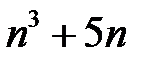ділиться на .

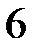9. 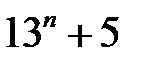ділиться на .

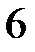10. 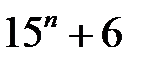ділиться на .

11. 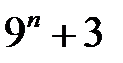ділиться на .

12. 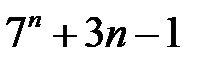ділиться на .

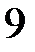13. 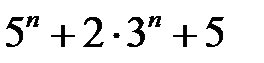ділиться на .

14. 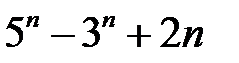ділиться на .

15. ділиться на .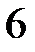

16. 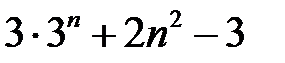ділиться на .

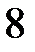17. 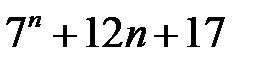ділиться на .

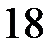18. 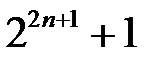ділиться на .

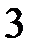19. 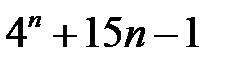ділиться на .

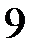20. 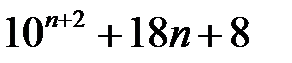ділиться на .

21. 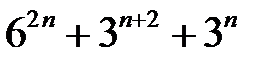ділиться на .

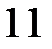22. 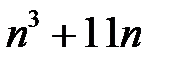ділиться на .

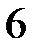23. 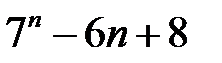ділиться на .

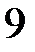24. 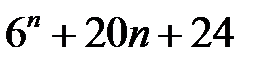ділиться на .

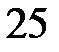25. 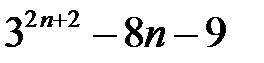ділиться на .

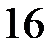26. 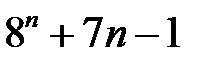ділиться на .

27. ділиться на .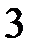

28. 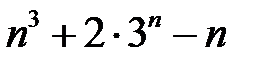ділиться на .

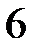29. 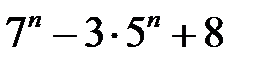ділиться на .

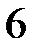30. 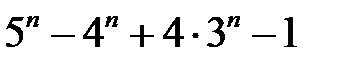ділиться на .

Завдання 3

Довести методом математичної індукції нерівності:

1.

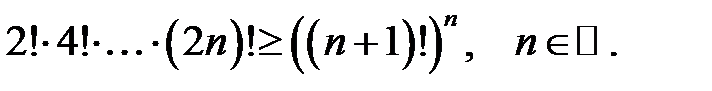
2.

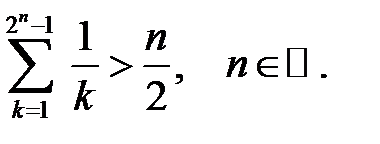
3.

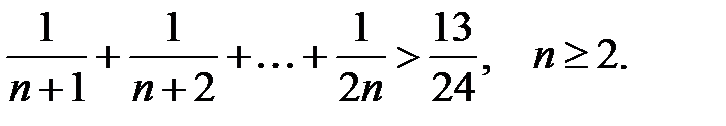
4.

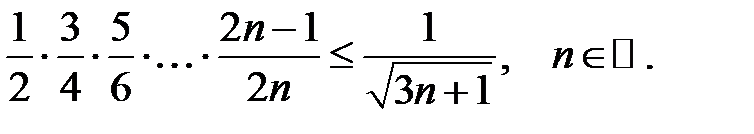
5.

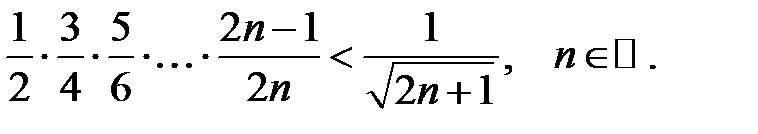
6.

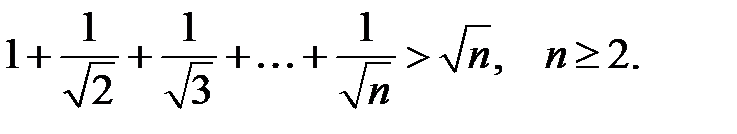
7.

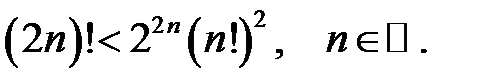
8.

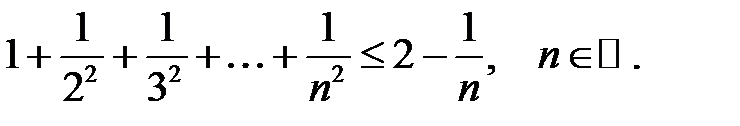
9.

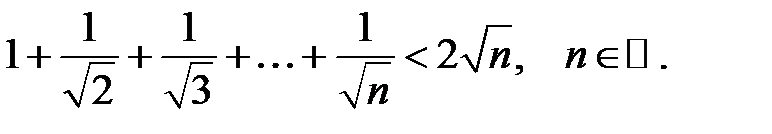
10.

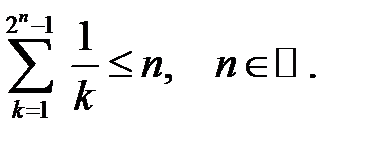
11.

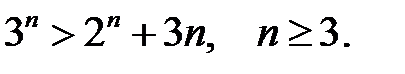
12.

13.

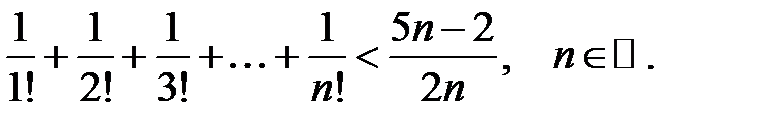
14.

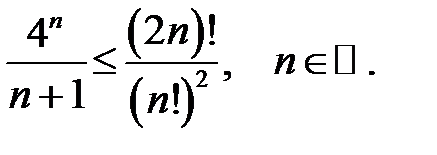
15.

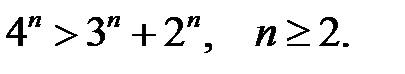
16.

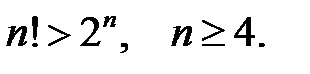
17.

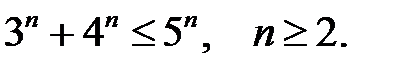
18.

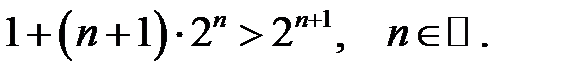
19.

20.

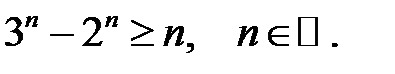
21.

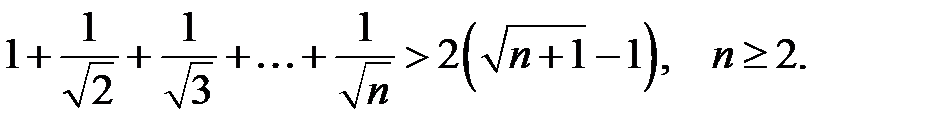
22.

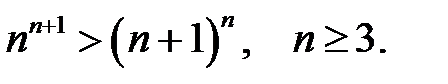
23.

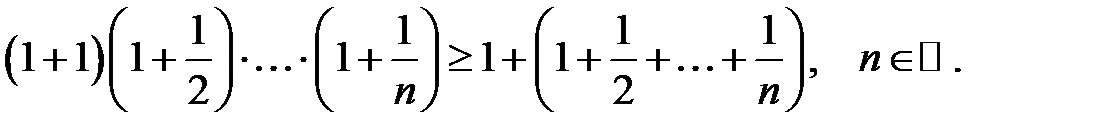
24.

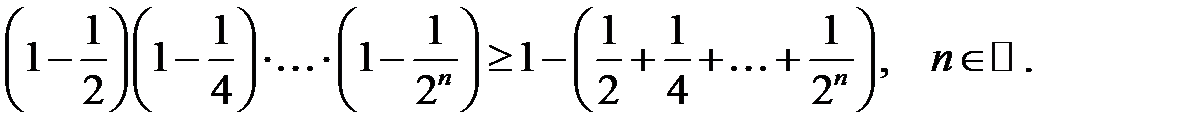
25.

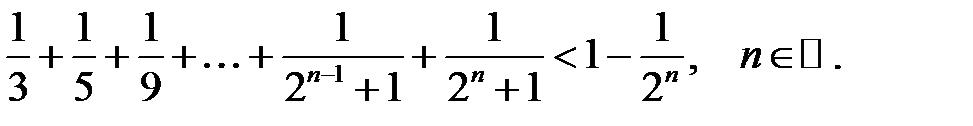
26.

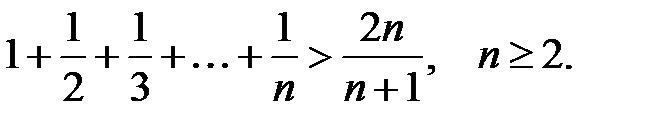
27.

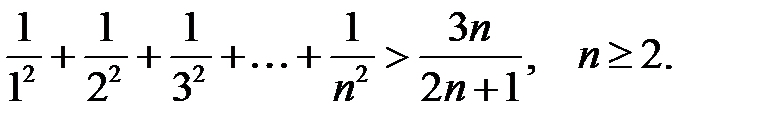
28.

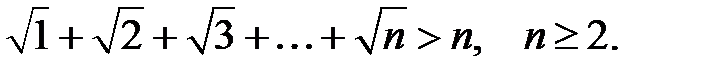
29.

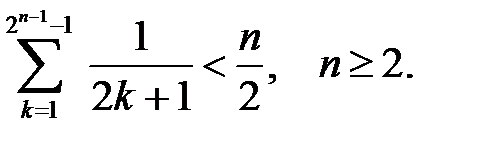
30.

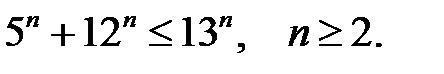
Читайте також:

1. Економічна і математична постановка задачі нелінійного програмування
2. Економічна і математична постановка задачі нелінійного програмування
3. Економічна і математична постановка ТЗ. Умови існування розв’язку ТЗ.
4. Економічна і математична постановка цілочислової задачі лінійного програмування
5. Електричний заряд. Електричне поле. Закон Кулона. Напруженість та індукція електричного поля. Принцип суперпозиції електричних полів
6. Електромагнітна індукція
7. Електромагнітна індукція
8. ЕЛЕКТРОМАГНІТНА ІНДУКЦІЯ В РУХОМОМУ ПРОВІДНИКУ
9. Ембріональна індукція. Морфогенез.
10. Загальна математична постановка задачі стохастичного програмування
11. Загальна характеристика задач розпізнавання образів та математична модель задачі
12. Індукція і репресія

Переглядів: 5651