
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Традуктивні умовиводи.
1. Умовні і розділові силогізми. Умовиводи створюються не лише з простих, але також із складних суджень, які належать до опосередкованих дедуктивних умовиводів. Серед видів опосередкованих дедуктивних умовиводів виділяють: умовні і розділові. Особливість цих умовиводів полягає в тому, що виведення наслідку з засновків визначається не відношеннями між термінами, як в категоричному силогізмі, а характером логічної зв'язки між судженнями.
Умовний умовивід (силогізм) – це опосередкований дедуктивний умовивід, до складу якого входять умовні судження, і перший засновок завжди є умовним.
Умовні силогізми підрозділяються на:
1) чисто умовні силогізми – це силогізми, в яких усі засновки і висновки є умовними судженнями:
Структура: Якщо A, то B Схема: a→b
Якщо B, то C b→с
Якщо A, то C a→c
Формула: ((a→b)  (b→с))→(a→c)
(b→с))→(a→c)
Якщо буде реалізований товар (a), то будуть гроші (b).
Якщо будуть гроші (b), то можлива угода на новий товар (c).
Якщо буде реалізований товар (a), то можлива угода на новий товар (c).
2) умовно-категоричні силогізми – це силогізми, де один засновок – умовне судження, а інший – просте категоричне судження і висновок є категоричним судженням.
В умовно-категоричних силогізмах два правильні модуси:
– стверджувальний модус (modus ponens), в якому міркування спрямоване від стверджування підстави до стверджування наслідку:
Структура: Якщо A, то B Схема: a→b
Aа
B b
Формула: ((a→b)  a)→b – є закон логіки.
a)→b – є закон логіки.
Можна будувати достовірні умовиводи від ствердження підстави
до ствердження наслідку:
Якщо цей метал ртуть (a), то він отруйний (b).
Цей метал – ртуть (a).
Цей метал отруйний (b);
– заперечувальний модус (modus tollens), в якому міркування спрямоване від заперечення наслідку до заперечення підстави:
Структура: Якщо A, то B Схема: a→b
Не-B ~b
Не-A ~a
Формула: ((a→b)  ~b)→~a – є закон логіки.
~b)→~a – є закон логіки.
Можна будувати достовірні умовиводи від заперечення наслідку
до заперечення підстави:
Якщо річка вийшла з берегів (a), то вода заливає прилеглі території (b).
Вода річки не заливає прилеглі території (не-b).
Річка не вийшла з берегів (не-a).
Два інші модуси дають імовірнісні висновки:
Перший модус:
Структура: Якщо A, то B Схема: a→b
Bb
Імовірно, A Імовірно, а
Формула: ((a→b)  b)→a – не є закон логіки.
b)→a – не є закон логіки.
Неможливо отримати достовірний висновок
йдучи від ствердження наслідку до ствердження підстави:
Якщо це тіло – графіт (a), то воно електропровідне (b).
Це тіло електропровідне (b).
Імовірно, це тіло – графіт (a).
Другий модус:
Структура: Якщо A, то B Схема: a→b
Не-A ~a
Імовірно, не-B Імовірно, не-b
Формула: ((a→b)  ~a)→~b – не є закон логіки
~a)→~b – не є закон логіки
Неможливо отримати достовірний висновок
йдучи від заперечення підстави до заперечення наслідку:
Якщо тіло піддати тертю (a), то воно нагріється (b).
Тіло не піддали тертю (не-a).
Імовірно, тіло не нагрілося (не-b);
3) умовно-розділові (лематичні, від грец. λημμα –припущення, посилання) умовиводи – це умовні умовиводи, які включають умовні і розділові (одне або два) судження.
Залежно від кількості альтернатив (від лат. alternare – чергування; тобто від числа членів у розділовому засновку), наявних в умовиводі, бувають такі види лематичних умовиводів: дилеми (від грец. δι – двічі і λημμα – припущення) і полілеми (від грец. πολυ – багато і λημμα – припущення).
Лематичні силогізми:
– Дилема – це умовно-розділовий силогізм, який містить дві альтернативи.
Два види дилем: конструктивні (від лат. constructivus – що служить для побудови) і деструктивні (від лат. destructivus – руйнівний), кожна з яких може бути простою і складною.
Проста конструктивна дилема – це умовно-розділовий силогізм, в якому перший (умовний) засновок стверджує, що з двох різних підстав випливає один і той же наслідок; другий засновок є диз'юнктивним судженням і стверджує, що одна або друга з підстав істинна; у висновку стверджується наслідок.
У простій конструктивній дилемі думка рухається від ствердження істинності підстав до ствердження істинності одного наслідку:
Схема: a→b, c→b, aÚc Формула: ((a→b)  (c→b)
(c→b)  (aÚc))→b – закон логіки
(aÚc))→b – закон логіки
b
Якщо студент відвідує зайняття в університеті (a), то він отримує знання (b).
Якщо студент читає навчальну літературу (c), то він отримує знання (b).
Студент або відвідує зайняття в університеті (a), або
читає навчальну літературу (c).
Студент отримує знання (b).
Складна конструктивна дилема – це умовно-розділовий силогізм, в якому перший засновок має дві підстави, з яких випливає два наслідки; другий (диз'юнктивне судження) стверджує істинність одного або другого наслідку; обидва наслідки її першого (умовного) засновку є різними.
У складній конструктивній дилемі думка рухається від ствердження істинності підстав до ствердження істинності двох наслідків:
Схема: a→b, c→d, aÚc Формула: ((a→b)  (c→d)
(c→d)  (aÚc))→(bÚd)
(aÚc))→(bÚd)
bÚd
Якщо людина порушила статут організації (а),
то вона притягується до дисциплінарної відповідальності (b).
Якщо людина вчинила суспільно небезпечне діяння (c),
то вона підлягає кримінальному покаранню (d).
Ця людина порушила статут організації (a)
або вчинила суспільно небезпечне діяння (c).
Ця людина притягується до дисциплінарної відповідальності (b)
або підлягає кримінальному покаранню (d).
Проста деструктивна дилема – це умовно-розділовий силогізм, в якому перший (умовний) засновок вказує на те, що з одного і того ж засновку випливають два різні наслідки; другий засновок є диз'юнктивним запереченням обох цих наслідків; у висновку заперечується засновок.
У простій деструктивній дилемі думка рухається від заперечення наслідків до заперечення підстави при одному антецеденті:
Схеми: a→b, a→c, ~bÚ~c Формули: ((a→b)  (a→c)
(a→c)  (~bÚ~c))→~а
(~bÚ~c))→~а
~а
Якщо людина закінчила навчання у ВНЗ (a),
то вона отримала вищу освіту (b).
Якщо людина закінчила навчання у ВНЗ (a),
то вона отримала професію за фахом (c).
Ця людина не отримала ні вищої освіти (не-b),
ні професії за фахом (не-c).
Ця людина не закінчила навчання у ВНЗ (не-a).
Складна деструктивна дилема – це умовно-розділовий силогізм, що містить один засновок, який складається з двох умовних суджень з різними засновками і різними наслідками; другий засновок є диз'юнкцією заперечення обох наслідків; висновок є диз'юнкцією заперечення обох засновків.
У складній деструктивній дилемі думка рухається від заперечення наслідків до заперечення підстав:
Схема: a→b, c→d, ~bÚ~d Формула: ((a→b)  (c→d)
(c→d)  (~bÚ~d))→(~aÚ~c)
(~bÚ~d))→(~aÚ~c)
~aÚ~c
Якщо людина обов'язкова (a), то вона завжди виконає свою обіцянку (b).
Якщо людина ввічлива (c), то вона, порушивши обіцянку, завжди вибачиться (d).
Ця людина або не завжди виконає свою обіцянку (не-b),
або, порушивши її, не завжди вибачиться (не-d).
Ця людина необов'язкова (не-a) або неввічлива (не-c).
– Трилема – це умовно-розділовий силогізм, який містить три альтернативи. Два види трилем: конструктивні і деструктивні, кожна з яких може бути простою і складною.
– Полілема(більше трьох альтернатив).
Розділовий умовивід (силогізм) – це опосередкований дедуктивний умовивід, в якому один або декілька засновків є розділовими судженнями, а перший засновок у ньому завжди є розділовим.
Розділові силогізми підрозділяються на:
1) чисто розділові силогізми – це силогізми, в яких обидві (або всі) засновки – розділові судження.
Структура: S є або A, або B, або C Схема: aÚbÚc, a→(a  Úa
Úa  )
)
A є або A  , або A
, або A  a
a  Úa
Úa  ÚbÚc
ÚbÚc
S є або A  , або A
, або A  , або B, або C
, або B, або C
Формула: [(aÚbÚс)  (а→(a
(а→(a  Úa
Úa  ))]→(a
))]→(a  Úa
Úa  ÚbÚc)
ÚbÚc)
У першому розділовому судженні кожне з трьох простих суджень : S є A, S є B, S є C – називають альтернативою. З судження «S є A» утворюються ще дві альтернативи, що становлять два члени нової диз'юнкції:
Будь-яка філософська система (s) є або ідеалістичною (a),
або матеріалістичною (b), або дуалістичною (c).
Ідеалістична система (a) є
або об'єктивним (a  ), або суб'єктивним ідеалізмом (a
), або суб'єктивним ідеалізмом (a  ).
).
__ __
Будь-яка філософська система (s) є
або об'єктивно-ідеалістичною (a  ), або суб'єктивно-ідеалістичною(a
), або суб'єктивно-ідеалістичною(a  ),
),
або матеріалістичною (b), або дуалістичною (c);
2) розділово-категоричні силогізми – це силогізми, де один із засновків якого – розділове, а інший – категоричне судження.
У розділово-категоричному силогізмі два правильні модуси:
– стверджувально-заперечувальний (modus ponendo tollens):
Структура: S є або A, або B Схема: a 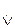 b, а або a
b, а або a 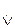 b, b
b, b
‑‑ ‑‑
S є A ~b ~a
S не є B
Формули: ((a 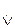 b)
b)  a)→~b; ((a
a)→~b; ((a 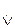 b)
b)  b)→~a – є закони логіки;
b)→~a – є закони логіки;
((aÚb)  a)→~b; ((aÚb)
a)→~b; ((aÚb)  b)→~a – не є закони логіки.
b)→~a – не є закони логіки.
Цей літак (s) або дозвуковий (a), або надзвуковий (b).
Цей літак (s) дозвуковий (a).
Цей літак (s) не надзвуковий (не-b).
– заперечувально-стверджувальний(modus tollendo ponens):
Структура: S є або A, або B
S не є A
S є B
Схеми: a b,~a a
b,~a a b,~b a
b,~b a b,~a a
b,~a a b,~b
b,~b
‑ ‑‑‑
b а bа
Формули: ((a b)
b)  ~a)→b; ((a
~a)→b; ((a b)
b)  ~b)→a – є закони логіки;
~b)→a – є закони логіки;
((a 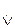 b)
b)  ~a)→b; ((a
~a)→b; ((a 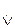 b)
b)  ~b)→a – є закони логіки.
~b)→a – є закони логіки.
Системи (s) бувають або матеріальні (a), або абстрактні (b).
Ця система (s) не є матеріальною (не-a).
Ця система (s) є абстрактною (b).
Обов'язковою умовою відносно висновків у розділово-категоричному умовиводі є те, що в розділовому засновку мають бути передбачені усі можливі альтернативи, тобто ділення має бути повним.
3) розділово-умовні силогізми – це умовиводи, де один (перший) із засновків є розділовим судженням, а інші засновки є умовними судженнями; кількість інших засновків дорівнює кількості членів розділового судження-засновку.
Структура: S є або A, або B Схема: aÚb, a→d, b→e
Якщо A, то D d e
e
Якщо B, то E
S є або D, або E
Формула: ((a b)
b)  (a→d)
(a→d)  (b→e))→(d
(b→e))→(d e)
e)
Для отримання знань (s) необхідно
або вчитися в навчальному закладі (a), або вчитися самостійно (b).
Щоб вчитися в навчальному закладі (a), необхідно вступити до нього (d).
Щоб вчитися самостійно (b)
треба самому шукати необхідну інформацію (e).
Для отримання знань (s) треба
або вступити до навчального закладу (d)
або самому шукати необхідну інформацію (e).
2. Індуктивні умовиводи. Принципово інший вид умовиводу – це індуктивний умовивід.
Індуктивний умовивід:
– це метод виробництва загального знання з часткових або одиничних засновків, на відміну від спрямованості думки в дедуктивному умовиводі – від загального до часткового;
– спирається на емпірично спостережувані предмети, які (або їх ознаки) в дедуктивному умовиводі можуть бути присутніми як менший засновок, що не є логічно необхідним;
– дає висновки різного ступеня імовірності, що не заперечує їх логічної правильності, тоді як дедуктивний умовивід визнається логічно правильним тільки у разі демонстративного, тобто логічно необхідного характеру висновку;
– припускає множину суджень-засновків, тобто кількість елементів може бути не визначена точно або бути актуально нескінченою, а дедуктивний умовивід (простий силогізм) завжди є висновок з двох засновків-суджень;
– усі засновки індуктивного умовиводу – рівнозначні, тобто між засновками відсутня відмінність за ступенем загальності (перший засновок, другий, третій і т.д. у будь-якій послідовності), а в дедуктивному умовиводі завжди визначаються більший і менший засновки;
– зв'язок між термінами висновку даний безпосередньо і в кожному засновку, а в дедуктивному умовиводі зв'язок між термінами висновку – S і Р, які є крайніми, не даний ні в одному з засновків, тут зв'язок встановлюється тільки у висновку завдяки відношенню кожного з цих термінів до середнього терміну, присутнього і в одному, і в інших засновках.
Індуктивний умовивід здійснюється за допомогою індукції.
Індукція: в широкому розумінні – це умовивід, в якому думка рухається від знань про одиничне до знань про загальне; у вузькому – це форма правдоподібного умовиводу, в якому на основі знань, відображених у засновках про окремі предмети певної множини, отримують висновок про усю множину (клас) предметів:
S (є) має ознаку Р
S (є) має ознаку Р
S (є) має ознаку Р
...........................................
S (є) має ознаку Р
S  ,S
,S  ,S
,S 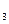 ... S
... S  належить класу (
належить класу (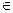 ) К
) К
Імовірно, кожен елемент класу К має ознаку Р ( S є Р).
Серед видів індукції виділяють повну, неповну і математичну.
Повна індукція – це такий умовивід, в якому загальний висновок про усі елементи класу предметів робиться на підставі розгляду кожного елементу цього класу, тобто вивчаються усі предмети цього класу, а засновками служать або одиничні, або загальні судження:
Формула: А  – а
– а
А  – а
– а
А 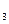 – а
– а
..........
А  – а
– а
А  , А
, А  , А
, А 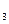 ... А
... А  – а (тобтоА
– а (тобтоА  , А
, А  ,А
,А 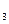 ... А
... А  вичерпують клас а).
вичерпують клас а).
‑_
Отже, усі А – а (тобто повна індукція дає достовірні результати, які, однак, не містять нічого нового).
Формула повної індукції в символічній логіці:
Р (х  )
)
Р (х  )
)
Р (х 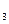 )
)
..........
Р (х  )
)
< х  , х
, х  , х
, х 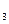 ... х
... х  >
> 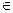 К
К
_‑‑
"х ((х 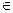 К)→Р(х))
К)→Р(х))
Формула читається: «Елементи х  , х
, х  , х
, х 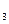 ... х
... х  мають ознаку Р. Кінцева множина цих елементів складає клас К. Отже, ознака Р належить усім елементам класу К».
мають ознаку Р. Кінцева множина цих елементів складає клас К. Отже, ознака Р належить усім елементам класу К».
Олексій (А  ) вчиться добре з математики (а).
) вчиться добре з математики (а).
Олена (А  ) вчиться добре з математики (а).
) вчиться добре з математики (а).
Олег (А 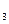 ) вчиться добре з математики (а).
) вчиться добре з математики (а).
...............................................................
і так про кожного із студентів цієї групи (А  , А
, А  , А
, А 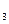 … А
… А  ),
),
що навчаються добре з математики (а).
Усі студенти(А) цієї групи вчаться добре по математиці (а).
Висновки повної індукції мають достовірний характер, оскільки в цьому випадку досліджуються усі предмети певної множини. Якщо засновки такого умовиводу є істинними, то і його висновок теж має бути істинним. Повна індукція використовується тільки при пізнанні закінчених класів. На відміну від дедукції, яка має теж достовірний характер, повна індукція не дає знань про інші предмети, окрім тих, які мисляться в одиничних судженнях-засновках.
Неповна індукція – це умовивід, в якому на підставі повторюваності ознаки у деяких елементів множини (класу) робиться висновок про її приналежність усім елементам:
Формула: А  – а
– а
А  – а
– а
А 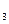 – а
– а
..........
А  – а
– а
...........
Отже, імовірно, що всі А – а (тобто неповна індукція, навпаки, дає результати, які є новими, але не достовірними, а лише імовірними).
Формула неповної індукції в символічній логіці:
Р (х  )
)
Р (х  )
)
Р (х 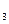 )
)
..........
Р (х  )
)
х  , х
, х  , х
, х 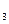 ... х
... х  ÌК
ÌК
_‑‑
"х ((х 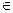 К)→Р(х))
К)→Р(х))
Формула неповної індукції відрізняється від повної тим, що множина, або клас, що охоплюється неповною індукцією, є відкритим, внаслідок чого перераховані елементи, що мають фіксовану у засновках і висновку ознаку, складають лише частину або підмножину класу, що зачіпається індукцією.
У цій групі вчиться 20 студентів.
Встановлено, що 18 з них добре склали іспит з історії.
Двоє інших не складали або невідомо, як вони його склали.
На підставі наявної інформації робиться висновок, що
уся група склала іспит добре.
Застосовується, коли, не спостерігаючи усі випадки досліджуваного явища (вони усі невідомі, їх багато, або їх вивчення неможливе), робиться висновок для усіх випадків. Але висновок не є достовірним, тому що, як у наведеному прикладі, не можна стверджувати, що інші студенти, відносно яких немає інформації, теж склали іспит добре. Отже, висновок може бути як істинним, так і неістинним. У той же час, неповна індукція призводить до розширення знання, оскільки ознака, що притаманна відомим явищам, поширюється на область невідомого, емпірично недослідженого. Для підвищення висновку неповної індукції застосовуються спеціальні методи, залежно від яких виділяють три види неповної індукції.
Три види неповної індукції: популярна (або перелічувальна), селективна (від. лат. selectio – вибір, відбір; або індукція через аналіз і відбір фактів) і наукова:
– популярна (перелічувальна) індукція – це індукція, при якій предмети з досліджуваною ознакою перераховуються підряд, у порядку їх появи у сфері чуттєвого сприйняття суб'єкта, або випадковим чином і якщо одна й та ж ознака повторюється у ряді однорідних предметів і відсутній випадок, що суперечить, то робиться загальний (імовірний, а не достовірний) висновок, що ця ознака властива усім предметам цього роду.
Так, довгий час європейці вважали, що лебеді можуть бути тільки білими. Проте це представлення було спростоване, коли в Австралії в 17 ст. були виявлені й чорні лебеді;
– селективна індукція (індукція через аналіз і відбір фактів) – це індукція, де спостереження предметів виключає випадкові висновки, оскільки вивчаються планомірно і цілеспрямовано відібрані, найбільш типові випадки, на основі певної системи критеріїв – кількісний (прикладів спостережуваних предметів повинно бути якомога більше) і якісний (умови фіксації, різноманітність у просторово-часовому і функціональному відношеннях і т.д.).
Наприклад, для отримання репрезентативного, науково обґрунтованого висновку, недоцільно опитувати усю генеральну сукупність, тобто сукупність усіх можливих соціальних об'єктів. Досить правильно зробити вибірку, обмеживши число респондентів з тим, щоб воно забезпечувало помилку висновку, що не перевищує допустимої погрішності;
– наукова індукція – це індукція, в якій на підставі встановлення суттєвих ознак або необхідних (в першу чергу, причинних) зв'язків між предметами класу робиться (достовірний) загальний висновок про усі предмети цього класу.
Наукова індукція припускає використання спеціальних методів, які базуються на поєднанні власне індукції і принципу одноманітності причин і їх наслідків. Наукова індукція названа по іменах розробників її методів – індукція Ф.Бекона-Дж.С.Мілля.
Методи індуктивної логіки (методи встановлення причинних зв'язків) засновані на знанні і використанні загальних рис причинного зв'язку, серед яких необхідно назвати такі:
2) кожне явище світу має причину, яку можна і треба встановити;
2) явище-причина настає в часі раніше, ніж явище-наслідок;
3) після явища-причини неодмінно настає явище-наслідок;
4) за відсутності явища-причини явище-наслідок не настає;
5) зміни в причині призводять до відповідних змін в наслідку.
Основні методи встановлення причинних зв'язків:
| <== попередня сторінка | | | наступна сторінка ==> |
| Література | | | I. Метод єдиної подібності. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |