
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лекція 1 Вступ. Основні поняття.
Теорія алгоритмів
Конспект лекцій
Частина 1
Чернівці
Чернівецький національний університет
УДК 510.51
Теорія алгоритмів: Конспект лекцій. Частина 1/ Укл: Ю.П. Стецько В.В. Лазорик, Е.О. Стецько – Чернівці: Золоті литаври, 2013. – 28 с.
Посібник містить теоретичні відомості з курсу теорія алгоритмів, які знайомлять студентів із різними формальними уточненнями базового поняття теорії програмування – алгоритму і його властивостями та дозволяють набути практичних навиків застосування теоретичних знань у практичній діяльності.
Для студентів, що здобувають освіту в галузі знань «Інформатика і обчислювальна техніка» та інших спеціальностей із поглибленим вивченням інформатики.
Друкується за ухвалою вченої ради факультету комп’ютерних наук Чернівецького національного університету імені Юрія Федьковича.
Укладачі: Стецько Юрій Павлович,кандидат фізико-математичних наук,
доцент кафедри математичних проблем управління і кібернетики (відповідальний за випуск),
Лазорик Василь Васильович,кандидат фізико-математичних наук,
доцент кафедри математичних проблем управління і кібернетики,
Стецько Елеонора Орестівна,асистент кафедри математичних проблем управління і кібернетики.
Підписано до друку 31.08.2013. Формат 60х84/16.
Папір газетний. Друк офсетний. Ум. друк. арк. 1.8. Обл. –вид. арк. 1.9.
Зам. 425. Тираж 50 прим.
Видавництво «Золоті литаври», м. Чернівці, вул. Заводська, 26а.
Лекція 1 Вступ. Основні поняття.
План:
1.Предмет та мета курсу.
2.Означення алгоритму, АОФ. Властивості алгоритму.
3.Класифікація формальних моделей алгоритму.
4.Поняття числення, формальної системи і їх зв’язок з поняттям алгоритму.
5. Універсальні класи алгоритмів. Формалізація поняття алгоритму.
Література:[1], [2], [10].
Процеси, які носять алгоритмічний характер відомі людству з глибокої давнини (знаходження НСД, правила виконання арифметичних дій над цілими числами і т. п.). Саме поняття алгоритму належить до базових понять математики, таких як натуральне число чи множина.
На інтуїтивному рівні, під алгоритмом розуміють деяку систему точно визначених правил для чисто механічного розв’язування задач певного класу.
З метою уточнення цього інтуїтивного означення алгоритм наділяють певними властивостями . До основних із них належать:
1. Фінітність, або скінченність процесу виконання алгоритму.
2. Масовість, тобто алгоритм призначений не для однієї задачі, а для певного класу задач.
3. Дискретність, тобто розбиття виконання алгоритму на окремі дискретні кроки.
4. Елементарність кроків алгоритму.
5. Детермінованість, або однозначність виконання алгоритмічного процесу.
6. Результативність – алгоритм має засоби, які через певну кількість кроків дозволяють отримати розв’язок задачі і зупинити його виконання.
Для опису алгоритму необхідно вказати множину його початкових даних X і множину даних Y до яких може належати результат . Алгоритм із множиною вхідних даних X і множиною вихідних даних Y прийнято називати X-Y алгоритмом.
Ведемо у розгляд ще декілька важливих для теорії алгоритмів понять.
Функцію будемо називати алгоритмічно обчислювальною (АОФ), якщо існує алгоритм, який її обчислює.
Множину L будемо називати алгоритмічно перелічною, якщо вона є областю значень деякої АОФ. Іншими словам, якщо існує алгоритм, який перелічує елементи цієї множини і тільки їх.
Множину L будемо називати алгоритмічно розв’язною відносно деякої множини S, якщо існує алгоритм, який дозволяє для кожного елемента множини S визначити чи цей елемент належить множині L, чи не належить їй.
Із поняттям алгоритму тісно пов’язане поняття числення. Це фундаментальне поняття відбиває і узагальнює інтуїтивну уяву про індуктивне породження об’єктів, яке широко розповсюджене в математиці.
Під численням розуміють скінчену множину точно визначених породжувальних правил, які дозволяють із певних заданих об’єктів одержувати інші об’єкти. Такі породжувальні правила називають, також, дозволяючими правилами, правилами виведення, допустимими підстановками.
Між поняттями числення і алгоритму існує як тісний зв’язок (кожне із цих понять в тому чи іншому сенсі можна звести до іншого), так і суттєві відмінності (зокрема, на відміну від наказових правил алгоритму, які однозначно визначають перехід від одних об’єктів до інших, правила числення тільки дозволяють перехід від одних об’єктів до інших).
З історичної точки зору поштовхом для виникнення теорії алгоритмів, як окремого розділу математики стали невдачі (початок 20-го століття) в знаходженні алгоритмів для, так званих, масових проблем (десята проблема Гільберта про розв’язність діофантових рівнянь, проблема істинності предикатів першого порядку і ін.). Стало зрозумілим, що для доведення не існування алгоритму розв’язку певної задачі інтуїтивного означення алгоритму недостатньо. Тому пошук точного формального математичного визначення алгоритму і вивчення на його основі загальних властивостей цього поняття став основною задачею теорії алгоритмів, як математичної дисципліни.
Пошук формальних уточнень поняття алгоритму проводився у двох напрямах.
1) Опис точного математичного поняття деякої ідеальної алгоритмічної машини та правил обчислюваності на ній. Першою формальною моделлю алгоритмічної машини була машина Тьюрінга, яка моделює елементарні дії при реалізації алгоритму людиною. Зараз відомо багато різновидностей машини Тьюрінга. Із більш пізніх формальних моделей згадаємо регістрові машини (Д. Шепердсон, Г. Стерджіс, 1963). До такого ж типу моделей відносяться нормальні алгоритми Маркова (А. Марков, 1952).
2)Опис певних класів функцій для яких існує алгоритм знаходження значення функції за значеннями її аргументів, тобто уточнюється не первісне поняття алгоритму, а похідне поняття алгоритмічно обчислюваної функції. Спочатку такі описи були запропоновані для функцій, заданих на множині натуральних чисел, пізніше - для функцій, заданих на множині інших об’єктів.
Першими формальними моделями алгоритмічно обчислюваних функцій були λ означувані функції (А.Чорч, 1932) та загально рекурсивні функції (К. Гьодель, 1934). Вказані класи функцій визначались як функції графіки яких породжуються, відповідно, численням конверсій та численням Ербана-Гьоделя. С. Кліні поширив поняття загально рекурсивної функції на випадок часткових функцій, ввівши поняття частково рекурсивної функції, та описав клас частково рекурсивних функцій в чисто функціональних термінах.
Для уточнення поняття числення вводять поняття формальної системи (скорочено ФС). Під формальною системою розуміють трійку ƒ = (L, A, P) , де L – мова формальної системи, А – множина аксіом, Р – множина правил виведення. Мова задається алфавітом і правилами побудови слів мови, які називаються формулами. Кожна аксіома є формулою. Правила виведення формальної системи діють на множині формул. Формула, яка одержується із аксіом за допомогою правил виведення, називається теоремою. Множину теорем формальної системи g позначатимемо Th(g). Правила виведення записуватимемо у вигляді P1…Pπ|-Р, де Р1…Р π – засновки, Р-висновок.
Під виведенням будемо розуміти скінчену послідовність формул В1…Вn таку, що кожна із формул послідовності або аксіома , або одержана із попередніх формул послідовності за допомогою деякого правила виведення.
Неважко переконатись,що формула є теоремою тоді і тільки тоді,коли вона має виведення.
ФС можна трактувати як числення із входом, в якому зафіксована множина початкових об’єктів, а породжувальні правила – суть правила виведення із Р. ФС можна також розглядати як числення із породжувальними правилами різного типу, які дозволяють відповідно породжувати формули, аксіоми і теореми та виділяти теореми як результативні об’єкти.
До формальних систем крім класичних аксіоматичних теорій, відносяться канонічні та нормальні системи Поста (Е. Пост,1943), формальні граматики (Н. Хомський,1952). Враховуючи розглянутий вище зв’язок між алгоритмами і численнями, формальні моделі алгоритмів та алгоритмічно обчислюваних функцій теж можуть бути задані у вигляді формальних систем.
Різні формальні моделі алгоритмів можуть діяти на різних множинах об’єктів. Наприклад, машини Тьюрінга та нормальні алгоритми діють на словах деякого алфавіту, регістрові машини діють на множині N натуральних чисел. Тому уточнимо поняття еквівалентності алгоритмів наступним чином.
Під кодуванням елементів множиниХ елементами множиниY будемо розуміти взаємно-однозначне відображення  :Х→Y таке, що множина
:Х→Y таке, що множина  (Х) розв’язна відносно множини Y.
(Х) розв’язна відносно множини Y.
Нехай αцеХ1-Y1―алгоритм, а β ― Х2-Y2―алгоритм. Нехай  -кодування елементівХ1,елементами Х2, Ψ -кодування елементів Y1 елементами Y2. Алгоритми α та β називаються еквівалентними з точністю до кодувань
-кодування елементівХ1,елементами Х2, Ψ -кодування елементів Y1 елементами Y2. Алгоритми α та β називаються еквівалентними з точністю до кодувань  , Ψ, якщо:
, Ψ, якщо:
1) α (а) = Ψ -1 ( β(  (a)) для кожного а, яке належитьХ1.
(a)) для кожного а, яке належитьХ1.
2) β (b) = Ψ (α (  -1 (b))) для кожного b,яке належитьX2 .
-1 (b))) для кожного b,яке належитьX2 .
Алгоритми α та βназиваються еквівалентними, якщо вони еквівалентні з точністю до деяких кодувань  та Ψ .
та Ψ .
Клас алгоритмів α називається універсальним, якщо кожний алгоритм еквівалентний деякому алгоритму із α. Аналогічно можна ввести поняття універсального класу числень .
Доведене в 1936 р. А. Чорчем та С. Кліні співпадання класів λ- визначених та загально рекурсивних функцій дало підставу А. Чорчу висунути тезу про про співпадання класів АОФ та загально рекурсивних функцій. Трохи пізніше С. Кліні поширив цю тезу на класи часткових функцій. Підтвердженням тези Чорча стало доведення співпадання класів частково рекурсивних функцій та функцій обчислювальних за Тьюрінгом. Пізніше такі співпадання були встановлені для всіх відомих формальних моделей АОФ. Тому є всі підстави вважати, що кожна із названих вище формальних моделей алгоритмів визначає універсальний клас алгоритмів.
Лекція 2. Машина Тьюрінга
План:
1.Поняття про машини Тьюрінга.
2.Структура та система команд машин Тьюрінга.
3.Приклади роботи машин Тьюрінга.
4. Функції обчислюванні за Тюрінгом.
Література: [2], [4], [10].
Англійський математик А.М.Тьюрінг запропонував 1936 р. клас абстрактних машин, які задають алгоритми, що можуть бути виконані людиною з олівцем і достатнім запасом паперу. Зараз відомо багато різних варіантів машин Тьюрінга та їх узагальнень (багатострічкові машини, машини з еластичною стрічкою і т.п.).
Зупинимось на такому визначенні машини Тьюрінга (МТ). Під МТ розумітимемо впорядковану п’ятірку (Q, Т, δ, q0, F), де
Q(q0 ,q1 ,…, qn) ― скінченна множина внутрішніх станів ;
Т(t1 ,…, tm) ― скінчений алфавіт символів стрічки, причому він обов’язково містить спеціальний символ пустої клітки λ ;
δ : Q × T→Q × T× {R, L, S} - функція переходів ;
q0  Q – початковий стан;
Q – початковий стан;
F  Q – множина фінальних станів .
Q – множина фінальних станів .
Функцію переходів δ на практиці задають скінченою множиною команд одного з трьох видів: qa→pbR, qa→pbL, qa→pbS, де p, q  Q; a, b
Q; a, b  T. При цьому, як правило, не для всіх пар (q, a )
T. При цьому, як правило, не для всіх пар (q, a )  Q × T існує команда з лівою частиною qa. Це означає, що функція δ не всюди визначена. Надалі ,eltv вважати, що δ всюди визначена, тому для всіх пар (q, a)
Q × T існує команда з лівою частиною qa. Це означає, що функція δ не всюди визначена. Надалі ,eltv вважати, що δ всюди визначена, тому для всіх пар (q, a)  Dδ неявно ( не додаючи відповідні команди виду qa→qa до множини команд) вводимо позначенняδ (q, a)=(q,a,ε).
Dδ неявно ( не додаючи відповідні команди виду qa→qa до множини команд) вводимо позначенняδ (q, a)=(q,a,ε).
Конструктивно МТ складається із пам’яті, яка утворена з нескінченної в обидва боки стрічки розділеної на клітки, пристрою керування та голівки читання – запису. В кожній клітинці стрічки міститься єдиний символ із алфавіту Т, причому, в кожен конкретний момент стрічка містить скінченну кількість символів, відмінних від символу λ . Голівка читання – запису у кожен дискретний момент оглядає єдину клітку стрічки.
Якщо МТ знаходиться в стані q і голівка читає символ а, то при виконанні команди qa → pbR ( команди qa → pbL, команди qa → pbS) МТ переходить в стан p, замість символу а записує на стрічці символ bі зміщує голівку на одну клітку вправо ( на одну клітку вліво, залишає голівку на місці ).
Конфігурація, або повний стан МТ – це слово виду xqy, де x, y  T* , q
T* , q  Q. Неформальне це означає, що на стрічці записане слово ху (зліва і справа від ху – тільки символи λ), МТ знаходиться в стані q , голівка читає перший символ під слова у.
Q. Неформальне це означає, що на стрічці записане слово ху (зліва і справа від ху – тільки символи λ), МТ знаходиться в стані q , голівка читає перший символ під слова у.
Конфігурацію виду q0x , де перший та останній символи слова х ,відмінні від λ, називають початковою. Конфігурацію виду xqy , де q  F , називають фінальною. Після переходу до фінального стану, тобто до фінальної конфігурації, МТ зупиняється . Машина Тьюрінга також зупиняється , якщо для певної конфігурації відповідна клітинка пуста (команда відсутня).
F , називають фінальною. Після переходу до фінального стану, тобто до фінальної конфігурації, МТ зупиняється . Машина Тьюрінга також зупиняється , якщо для певної конфігурації відповідна клітинка пуста (команда відсутня).
Нехай МТ знаходиться в конфігураціїxcqay, де x, y  T*, a,c
T*, a,c  T , q
T , q  Q.
Q.
Після виконання команди qa → pbL (команди qa → pbR , qa → pbS) MT перейде до конфігураціїxpcby (конфігурації xcbpy , xcpby ).
Кожна МТ задає деяке словникове відображення Т* → Т*. Будемо вважати, що деяка машина Тьюрінга М переводить слово u  T* в слово v
T* в слово v  T*, якщо вона з початкової конфігурації q0uпереходить до фінальної конфігурації xqy , де q
T*, якщо вона з початкової конфігурації q0uпереходить до фінальної конфігурації xqy , де q  F, xy = αvβ , α, β
F, xy = αvβ , α, β  {λ}* , причому перший та останній символи слова v відмінні від λ , або v=ε. Цей факт записуємо так: v=M(u). Якщо МТ М, починаючи роботу з початкової конфігурації q0u, ніколи не зупиняється, то кажуть, що М зациклюється при роботі над словом u. Тоді значеня М (u) не визначене.
{λ}* , причому перший та останній символи слова v відмінні від λ , або v=ε. Цей факт записуємо так: v=M(u). Якщо МТ М, починаючи роботу з початкової конфігурації q0u, ніколи не зупиняється, то кажуть, що М зациклюється при роботі над словом u. Тоді значеня М (u) не визначене.
Дві машини Тьюрінга М1 та М2 вважаються еквівалентними, якщо вони задають одне і те ж словникове відображення Т* → Т*.
МТ називається детермінованою, якщо функція δ однозначна. Інакше МТ називається не детермінованою .
Не обмежуючи загальності можна вважати , що множина F складається з єдиного фінального стану q*. Справді, нехай М =(Q,T,δ,q0,F). Візьмемо q*  Q. Тоді МТ М1 = (Q
Q. Тоді МТ М1 = (Q  {q*}, T, δ1, q0, {q*}),де δ1= δ
{q*}, T, δ1, q0, {q*}),де δ1= δ  {qa→q*a|q
{qa→q*a|q  F, a
F, a  T},очевидно, еквівалентна машині М.
T},очевидно, еквівалентна машині М.
Надалі розглядатимемо тільки детерміновані МТ з єдиним фінальним станом і позначатимемо їх (Q,T,δ,q0,q*). Конкретні МТ будемо задавати, вказуючи множину команд. При цьому початковий стан завжди позначатимемо q0, фінальний стан позначатимемо q*.
Машина Тьюрінга Мобчислює деяку часткову функцію  , якщо вона кожне слово виду
, якщо вона кожне слово виду  переводить в слово f(
переводить в слово f( ) у випадку
) у випадку 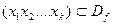 ,та машина Тьюрінга не визначена на цьому наборі, якщо
,та машина Тьюрінга не визначена на цьому наборі, якщо 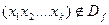 . Функція називається обчислювальною за Тьюрінгом, або МТ-обчислювальною, якщо існує МТ, яка її обчислює.
. Функція називається обчислювальною за Тьюрінгом, або МТ-обчислювальною, якщо існує МТ, яка її обчислює.
Наведемо приклади машини Тьюрінга .
Приклад 1. Машина Тьюрінга, яка реалізує функцію f(x,y)=x+y в алфафіті Т(1, λ,+) матиме вигляд:
| 1 | + | λ | |
| q0 | q1λR | q* λS | |
| q1 | q1 1R | q1+R | q21L |
| q2 | q21L | q2+L | q0 λR |
Тобто, якщо x=4, y=2, вхідне слово має вигляд 1111+11,
а фінальне слово 111111.
Приклад 2. Машина Тьюрінга, яка реалізує функцію f(x,y)=x-y в алфафіті Т(1, λ,-) матиме вигляд:
| 1 | - | λ | |
| q0 | q1λR | q* λS | |
| q1 | q1 1R | q1-R | q2 λL |
| q2 | q3 λ L | q* λS | |
| q3 | q3 1 L | q3-L | q0 λR |
Тобто, якщо x=5, y=2, вхідне слово має вигляд 11111-11,
а фінальне слово 111.
Читайте також:
- I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- II. Основні засоби
- II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
- II.3. Основні способи і прийоми досягнення адекватності
- III. Основні обов'язки робітників та службовців
- IV. Основні обов'язки адміністрації
- V. ОСНОВНІ ВИМОГИ ДО ОФОРМЛЕННЯ КУРСОВОЇ РОБОТИ
- VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
- Адвокатура в Україні: основні завдання і функції
- Амортизація основних засобів, основні методи амортизації
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
| <== попередня сторінка | | | наступна сторінка ==> |
| НАВЧАЛЬНЕ ВИДАННЯ | | | Лекція 3. Машини з натуральнозначними регістрами. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |