
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Практична робота № 5
Тема:Аналіз концентрації, диференціації та подібності розподілів
Мета практичної роботи:Закріпити на навчальних ситуаціях теоретичний матеріал за темою лекції “Аналіз концентрації, диференціації та подібності розподілів ”.
Контрольні запитання:
1. Різновиди та характеристики форм розподілів.
2. Оцінка і аналіз нерівномірності розподілів.
3. Оцінка подібності двох розподілів.
Практичні заняття з теми передбачають:
За сформованою сукупністю визначити:
1. Коефіцієнт асиметрії.
2. Коефіцієнт локалізації та коефіцієнт децильної диференціації.
3. Коефіцієнт концентрації Лоренца. Побудувати криву Лоренца.
Методичні вказівки до теми:
Різноманітність статистичних сукупностей – передумова різних форм співвідношення частот і значень варіативної ознаки. За формою розподіли поділяються на одно-, дво- і багатовершинні. Наявність двох і більше вершин свідчить про неоднорідність сукупності, про поєднання в ній груп з різними рівнями ознаки. Розподіл якісно однорідних сукупностей, як правило, одновершинні. Серед одновершинних розподілів є симетричні та асиметричні(скошені), гостро- і плоско вершинні:

Рис.5.1. Види розподілів
У симетричному розподілі рівновіддалені від центра значення ознаки мають однакові частоти, в асиметричному – вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини.Якщо вершина зміщена вліво, то ця асиметрія правостороння, і навпаки. Асиметрія виникає внаслідок обмеженої варіації в одному напрямі або за умови домінування причини розвитку, яка веде до зміщення центра розподілу.
Найпростішою мірою асиметричності розподілу є відхилення між характеристиками центра розподілу. Оскільки у симетричному розподілі  , то чим помітніша асиметрія, тим більше відхилення (
, то чим помітніша асиметрія, тим більше відхилення ( 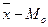 ). За правосторонньої асиметрії
). За правосторонньої асиметрії 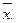 >
> 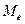 >
> 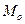 , за лівосторонньої, навпаки,
, за лівосторонньої, навпаки, 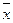 <
< 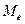 <
< 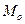 . Стандартне відхилення називають коефіцієнтом асиметрії (за Пірсоном) і визначають:
. Стандартне відхилення називають коефіцієнтом асиметрії (за Пірсоном) і визначають:
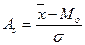 . (5.1)
. (5.1)
В симетричному розподілі 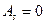 , у разі правосторонньої асиметрії
, у разі правосторонньої асиметрії  >0, лівосторонньої
>0, лівосторонньої  <0. Коефіцієнт асиметрії може набувати значень від
<0. Коефіцієнт асиметрії може набувати значень від
-3 до +3.
Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини і називається ексцесом.
Як узагальнені характеристики розподілу використовують моменти розподілу. Систему моментів розподілу розробив російський математик П.Л.Чейбишев. За допомогою невеликої їх кількості можна описати будь – який розподіл.
Момент розподілу – це середня арифметична k – го ступеня відхилень x-A:
 , (5.2)
, (5.2)
де, 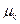 - момент k – го порядку; х – варіанта ряду; f – частота ряду; k і А – постійні числа.
- момент k – го порядку; х – варіанта ряду; f – частота ряду; k і А – постійні числа.
Залежно від значення А загальна система моментів ділиться на три підсистеми:
1) за А=0 отримують первинні моменти:
 ; (5.3)
; (5.3)
2) за 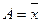 - центральні:
- центральні:
 (5.4)
(5.4)
3) за  , де
, де 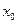 - деяка варіанта ряду, зазвичай близька до його середини, отримують умовні моменти
- деяка варіанта ряду, зазвичай близька до його середини, отримують умовні моменти
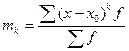 . (5.5)
. (5.5)
Первинний момент першого порядку є середня арифметична:  , другого –середній квадрат значень ознаки:
, другого –середній квадрат значень ознаки:  ; центральний момент другого порядку характеризує варіацію:
; центральний момент другого порядку характеризує варіацію: 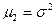 , тобто є дисперсією.
, тобто є дисперсією.
Якщо виразити первинні моменти через умовні, то отримаємо:
 .
.
Тоді первинні моменти перших чотирьох порядків:
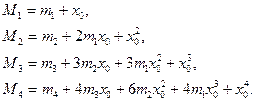 (5.6)
(5.6)
Якщо виразити центральні моменти через умовні, то:
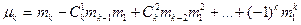 . (5.7)
. (5.7)
Звідси центральні моменти перших чотирьох порядків:
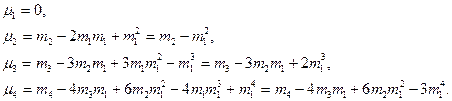 (5.8)
(5.8)
Центральні моменти третього і четвертого порядків використовуються для характеристики асиметрії та ексцесу розподілу.
Коефіцієнт асиметрії:  . (5.9)
. (5.9)
За правосторонньої асиметрії 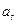 >0, за лівосторонньої
>0, за лівосторонньої 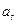 <0. Тому правосторонню асиметрію називають додатною, а лівосторонню – від’ємною. Вважають, що якщо
<0. Тому правосторонню асиметрію називають додатною, а лівосторонню – від’ємною. Вважають, що якщо 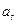 <0,25 – асиметрія низька, якщо
<0,25 – асиметрія низька, якщо 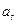 не перевищує 0,5 – середня і якщо
не перевищує 0,5 – середня і якщо 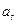 >0,5 – висока.
>0,5 – висока.
Для вимірювання ексцесу використовують коефіцієнт ексцесу:
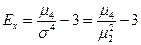 . (5.10)
. (5.10)
За гостро вершинного розподілу  >0, за плосковершинного
>0, за плосковершинного  <0.
<0.
Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупностей ґрунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності  та за обсягом значень ознаки
та за обсягом значень ознаки  . Якщо розподіл значень ознаки рівномірний, то
. Якщо розподіл значень ознаки рівномірний, то  =
=  . Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірюється коефіцієнтами:
. Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірюється коефіцієнтами:
- локалізації:  ; (5.11)
; (5.11)
- концентрації:  . (5.12)
. (5.12)
Коефіцієнт локалізації розраховується длякожної j-ї складової сукупності. За рівномірного розподілу всі значення 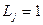 . У випадку концентрації значень ознаки в j – й складовій
. У випадку концентрації значень ознаки в j – й складовій  >1, і навпаки.
>1, і навпаки.
Коефіцієнт концентрації є узагальненою характеристикою відхилення розподілу від рівномірного. Значення його коливаються від 0 до 1; у рівномірному розподілі К=0, що помітніша концентрація, тим більше значення К відхиляється від 0.
Аналогічно побудований показник до коефіцієнта концентрації, який характеризує розподіл доходів між населенням країни чи регіону, називають коефіцієнтом Лоренца.
Цей розподіл доходів можна проілюструвати кривою Лоренца:
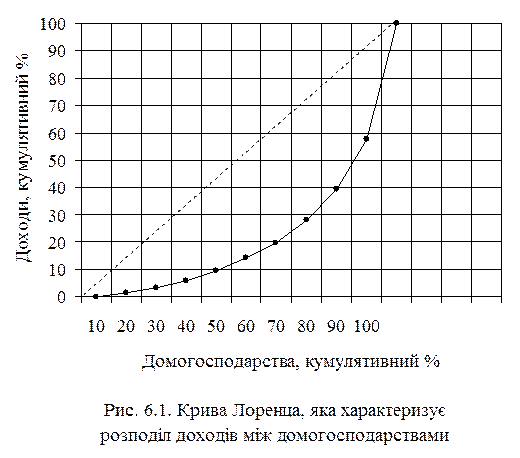
Мірою оцінки розшарування сукупності є коефіцієнт диференціації:
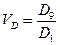 , (5.13)
, (5.13)
де 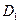 і
і 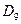 - відповідно перший і дев’ятий децимі.
- відповідно перший і дев’ятий децимі.
За аналогією з коефіцієнтом концентрації розраховують коефіцієнт подібності (схожості) структур двох об’єктів або одного об’єкта за двома ознаками:
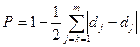 . (5.14)
. (5.14)
Якщо структури однакові, Р=1. Чим більші відхилення структур, тим меншим є значення коефіцієнта Р.
Нормальний розподіл близький до інших одновершинних розподілів. Він виражається формулою:
 , (5.15)
, (5.15)
де  - щільність ймовірності в розподілі випадкової величини або відносна щільність розподілу, по відношенню до варіаційного ряду; х – варіанти;
- щільність ймовірності в розподілі випадкової величини або відносна щільність розподілу, по відношенню до варіаційного ряду; х – варіанти; 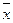 - їх середня арифметична;
- їх середня арифметична; 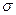 - середнє квадратичне відхилення; е і
- середнє квадратичне відхилення; е і  - математичні сталі.
- математичні сталі.
Нормальний розподіл повністю визначається двома параметрами: 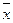 і
і 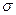 , тобто нормальні розподіли відрізняються між собою положенням на осі
, тобто нормальні розподіли відрізняються між собою положенням на осі 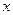 центра розподілу і розсіюванням варіант навколо цього центра.
центра розподілу і розсіюванням варіант навколо цього центра.
Функція нормованого відхилення (нормальної кривої) нормального розподілу має вигляд: 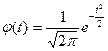 , (5.16)
, (5.16)
де  - функція нормованого відхилення;
- функція нормованого відхилення;  - відношення довжини кола до діаметра, яке становить 3,1416;
- відношення довжини кола до діаметра, яке становить 3,1416;  - основа натуральних логарифмів, що дорівнює 2,71828; t – нормоване відхилення
- основа натуральних логарифмів, що дорівнює 2,71828; t – нормоване відхилення 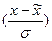 .
.
Існують таблиці значень  для будь –яких значень t.
для будь –яких значень t.
Побудова нормальної кривої за емпіричними даними здійснюється за формулою:  , (5.17)
, (5.17)
де 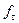 - теоретична частота кожного інтервалу (групи) розподілу; і – крок (величина) інтервалу;
- теоретична частота кожного інтервалу (групи) розподілу; і – крок (величина) інтервалу;  - сума частот інтервалу;
- сума частот інтервалу; 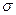 - середнє квадратичне відхилення;
- середнє квадратичне відхилення;  - функція нормованого відхилення.
- функція нормованого відхилення.
Між теоретичними і фактичними частотами можуть виникати розбіжності. Вони можуть бути випадковими, або наслідком невідповідності теоретичної кривої реальному характеру розподілу.
Об’єктивну оцінку наближеності емпіричних частот до теоретичних можна отримати за допомогою критеріїв узгодження. Найчастіше застосовується критерій Пірсона.
Критерій Пірсона (  ) обчислюють за формулою:
) обчислюють за формулою:
 , (5.18)
, (5.18)
де 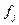 і
і  - відповідно емпіричні та теоретичні частоти j – ї групи; m – кількість груп у ряді розподілу.
- відповідно емпіричні та теоретичні частоти j – ї групи; m – кількість груп у ряді розподілу.
Для оцінки подібності емпіричного розподілу до теоретичного визначають ймовірність досягнення  даної величини
даної величини  при випадкових відхиленнях частот. Якщо
при випадкових відхиленнях частот. Якщо  >0,05 то відхилення фактичних частот від теоретичних можна вважати випадковими, якщо
>0,05 то відхилення фактичних частот від теоретичних можна вважати випадковими, якщо  <0,05 то відхилення не можна вважати випадковими, а емпіричний розподіл є принципово відмінним від розрахованого теоретичного.
<0,05 то відхилення не можна вважати випадковими, а емпіричний розподіл є принципово відмінним від розрахованого теоретичного.
Таблиці ймовірностей певних значень  розраховані для різної кількості ступенів вільності варіювання емпіричного ряду частот. При цьому кількість ступенів вільності k визначається:
розраховані для різної кількості ступенів вільності варіювання емпіричного ряду частот. При цьому кількість ступенів вільності k визначається:
 , (5.19)
, (5.19)
де m – кількість груп у сукупності; r – кількість параметрів функції теоретичного розподілу. Для нормального розподілу r = 2; k = m -3.
Розподіл Пуассона називають розподілом рідкісних явищ або малоймовірних подій. Він виражається формулою:
 , (5.20)
, (5.20)
де  - щільність ймовірності в розподілі випадкової величини;
- щільність ймовірності в розподілі випадкової величини; 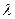 - середня кількість появи подій А в n однакових незалежних дослідах; m – частота події А.
- середня кількість появи подій А в n однакових незалежних дослідах; m – частота події А.
Побудова розподілу Пуасона за емпіричними даними практично не відрізняється від побудови нормального розподілу. На основі емпіричного розподілу визначають 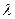 . Теоретичні частоти розраховують:
. Теоретичні частоти розраховують:
 , (5.21)
, (5.21)
де і – інтервал;  - сума частот; m – номер інтервалу (починаючи з m=0),
- сума частот; m – номер інтервалу (починаючи з m=0),  - його середня арифметична.
- його середня арифметична.
Типові задачі:
1. Інтервальний ряд розподілу за зростом 50 студентів має вигляд:
Таблиця 5.1
Розподіл студентів за зростом
| Зріст, см. | Кількість студентів, осіб | Накопичені частоти |
| 160 -165 | ||
| 165 -170 | ||
| 170 - 175 | ||
| 175 - 180 | ||
| 180 - 185 | ||
| 185 -190 | ||
| 190 -195 | ||
| Разом | х |
Розрахувати показники характеристики форм та подібності розподілів.
Розв’язання:
Розрахуємо коефіцієнт асиметрії за Пірсоном: 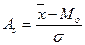 .
.
Для цього розрахуємо 

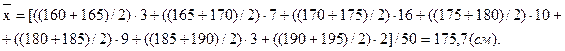
 .
.
 (см).
(см).
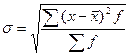 .
.
 (cм.)
(cм.)
Отже, 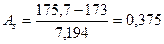 , що свідчить про незначну правосторонню асиметрію розподілу.
, що свідчить про незначну правосторонню асиметрію розподілу.
Знайдемо первинні моменти перших чотирьох порядків. Для цього складемо таблицю:
Таблиця 5.2
Допоміжні обчислення для спрощення розрахунків моментів розподілу
| Зріст, см | Кількість студентів, осіб, f | Середини інтервалів, x | 
| 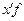
| 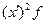
| 
| 
|
| 160 -165 | 162,5 | -3 | -9 | -81 | |||
| 165 -170 | 167,5 | -2 | -14 | -56 | |||
| 170 - 175 | 172,5 | -1 | -16 | -16 | |||
| 175 - 180 | 177,5 | ||||||
| 180 - 185 | 182,5 | ||||||
| 185 -190 | 187,5 | ||||||
| 190 -195 | 192,5 | ||||||
| Разом | х | х | -18 | -66 |
Умовні моменти: 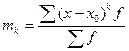 .
.

Первинні моменти перших чотирьох порядків:
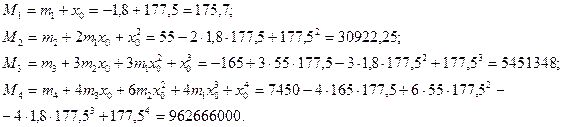
Центральні моменти перших чотирьох порядків:
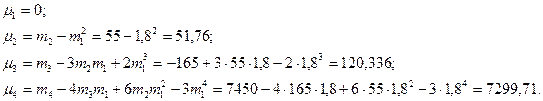
Звідси, 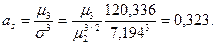
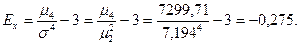
Отже, розподіл студентів за зростом є плоско вершинним і характеризується середньою правосторонньою (додатною) асиметрією.
Теоретичні частоти нормального розподілу студентів за зростом відображені в табл. 5.3.
Таблиця 5.3
Розрахунок теоретичних частот нормального розподілу студентів за зростом
| Зріст, см | Кількість студентів, осіб, f | Середини інтервалів, x | 
| 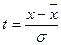
| 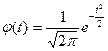
| 
|
| 160 -165 | 162,5 | -13,2 | -1,83 | 0,0748 | ||
| 165 -170 | 167,5 | -8,2 | -1,14 | 0,2083 | ||
| 170 - 175 | 172,5 | -3,2 | -0,44 | 0,3621 | ||
| 175 - 180 | 177,5 | 1,8 | 0,25 | 0,3867 | ||
| 180 - 185 | 182,5 | 6,8 | 0,95 | 0,2541 | ||
| 185 -190 | 187,5 | 11,8 | 1,64 | 0,1040 | ||
| 190 -195 | 192,5 | 16,8 | 2,34 | 0,0258 | ||
| Разом | х | х | х | х |
Як видно з порівняння отриманих 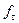 і фактичних частот
і фактичних частот  , розбіжності між ними порівняно незначні. Такі розбіжності можуть бути або випадковими або наслідком невідповідності теоретичної кривої реальному характеру розподілу.
, розбіжності між ними порівняно незначні. Такі розбіжності можуть бути або випадковими або наслідком невідповідності теоретичної кривої реальному характеру розподілу.
Визначимо критерій Пірсона:
Таблиця 5.4
Розрахунок критерію Пірсона:
| Зріст, см | Кількість студентів, осіб | 
| 
| |
| фактична f | теоретична 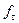
| |||
| 160 -165 | ||||
| 165 -170 | ||||
| 170 - 175 | 0,69 | |||
| 175 - 180 | -3 | 0,69 | ||
| 180 - 185 | ||||
| 185 -190 | -1 | 0,25 | ||
| 190 -195 | ||||
| Разом | х | 2,63 |
Звідси,  =2,63; k=7-3=4.
=2,63; k=7-3=4.
За таблицею ймовірностей  .
.
Отже, відхилення фактичних частот від теоретичних можна вважати випадковим, а сам розподіл студентів за зростом – подібним до нормального.
2.За наведеними даними визначити коефіцієнти концентрації та локалізації.
Таблиця 5.5
Дані про вартість реалізації продукції фермерськими господарствами району
| Вартість реалізованої продукції, тис.грн | % до підсумку | |
| кількості ферм | вартості реалізованої продукції | |
| До 20 | ||
| 20 – 50 | ||
| 50 – 100 | ||
| 100 – 200 | ||
| 200 – 400 | ||
| 400 і більше | ||
| Разом |
Складемо розрахункову таблицю:
Таблиця 5.6
Розрахункова таблиця
| Вартість реалізованої продукції, тис.грн | % до підсумку | 
| 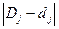
| |
| кількості ферм | вартості реалізованої продукції | |||
| До 20 | 0,17 | |||
| 20 – 50 | 0,28 | |||
| 50 – 100 | 0,52 | |||
| 100 – 200 | 1,12 | |||
| 200 – 400 | 2,87 | |||
| 400 і більше | 8,00 | |||
| Разом | х |
Коефіцієнт концентрації:  =
=  , що свідчить про відносно високий рівень концентрації товарного сільськогосподарського виробництва у фермерських господарствах. Обсяги товарної продукції концентруються у великих господарствах в останній групі (L=8,00).
, що свідчить про відносно високий рівень концентрації товарного сільськогосподарського виробництва у фермерських господарствах. Обсяги товарної продукції концентруються у великих господарствах в останній групі (L=8,00).
Завдання для самостійної роботи:
1.Використовуючи характеристики центра розподілу, сформулюйте висновки відносно наявності, напряму і ступеня асиметрії розподілу сімей в області за розміром:
| Кількість членів сім’ї, які проживають разом, осіб | Разом | ||||||
| Кількість сімей, % до підсумку |
2.За наведеними в таблиці даними, визначте коефіцієнт концентрації виробництва та робочої сили на спільних підприємствах і побудуйте графік концентрації Лоренца. Сформулюйте висновки.
| Група підприємств за чисельністю працівників | % до підсумку | ||
| кількості підприємств | чисельності працівників | обсягу виробництва | |
| До 50 | 51,4 | 9,9 | 15,7 |
| 50 – 200 | 34,7 | 29,7 | 36,4 |
| 200 – 600 | 10,7 | 30,1 | 25,2 |
| 600 – 1000 | 1,8 | 12,1 | 7,3 |
| 1000 і більше | 1,4 | 18,2 | 15,4 |
| Разом | 100,0 | 100,0 | 100,0 |
3.За наведеними даними обчисліть коефіцієнти галузевої локалізації експорту. Сформулюйте висновки.
| Галузь промисловості | % до підсумку | |
| загального обсягу виробництва | обсягу експорту товарів | |
| Харчова промисловість | 17,4 | 20,4 |
| Хімічна промисловість | 7,5 | 16,6 |
| Металургія | 23,5 | 32, 7 |
| Верстатобудування | 16,0 | 16,0 |
| Інші | 35,6 | 14,4 |
| Разом | 100,0 | 100,0 |
4.Розподіл вкладів громадян за їх розміром в одному з відділень Ощадбанку характеризуються даними:
| Розмір вкладу, грн | До1000 | 1000 - 2000 | 2000 - 3000 | 3000 - 4000 | 4000 - 5000 | 5000 - 6000 | 6000 і більше |
| Кількість вкладів |
Застосувавши функцію нормального розподілу, обчисліть теоретичні частоти і за допомогою критерію узгодження Пірсона перевірте подібність емпіричного розподілу до теоретичного з імовірністю 0,95. Сформулюйте висновки.
Література: основна [1-3, 7]
додаткова [ 5, 8, 9]
Практична робота №6
Тема:Статистичні методи вимірювання взаємозв’язків
Мета практичної роботи:Закріпити на навчальних ситуаціях теоретичний матеріал за темою лекції “ Статистичні методи вимірювання взаємозв’язків ”.
Контрольні запитання:
1. Види зв’язків між явищами. Суть стохастичної та кореляційної залежностей.
2. Модель аналітичного групування. Теоретичне обґрунтування моделі.
3. Оцінка лінії регресії. Вимірювання щільності зв’язку. Перевірка істотності зв’язку.
Практичні заняття з теми передбачають:
1. Побудувати модель аналітичного групування на підставі первинних
не згрупованих даних, а також даних комбінаційного розподілу.
Визначити оцінки лінії регресії та ефекти впливу.
2. Визначити дисперсії результативної ознаки, скориставшись правилом
розкладання дисперсії.
3. Оцінити щільність зв’язку за даними моделі аналітичного групування
та перевірити істотність зв’язку.
Методичні вказівки до теми:
Метод аналітичних групувань полягає у тому, що спочатку обирають факторну ознаку і результативну, потім проводять групування за факторною ознакою та обчислення середніх у кожній групі за результативною ознакою. Зіставленням характеру зміни факторної та результативної ознак можна дійти висновку про наявність зв'язку, його напрям та тісноту..
Кореляційний метод застосовується для вимірювання тісноти (щільності) зв'язків між ознаками за допомогою спеціальних співвідношень, що базуються на правилі додавання дисперсій. Ці співвідношення можна обчислити для кількісних ознак. Числові характеристики кореляційного зв'язку: кореляційне відношення; індекс кореляції; лінійний коефіцієнт кореляції.
Кореляційне відношення показує питому вагу міжгрупової дисперсії у загальній дисперсії, тобто визначає, наскільки тісний зв'язок факторної ознаки, за якою проводилося групування, та результативної ознаки.
Його позначають малою грецькою буквою 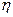 — («тета») і обчислюють за формулою:
— («тета») і обчислюють за формулою: 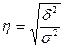 , (6.1)
, (6.1)
де 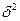 - міжгрупова дисперсія;
- міжгрупова дисперсія;  - - загальна дисперсія.
- - загальна дисперсія.
Кореляційне відношення змінюється від 0 до 1.
Чим ближче 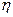 до 1, тим зв'язок між ознаками тісніший.
до 1, тим зв'язок між ознаками тісніший.
Індекс кореляції визначають зіставленням внутрішньогрупової дисперсії та загальної, позначають буквою R і обчислюють за формулою:
 , (6.2)
, (6.2)
де 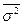 - внутрішньо групова дисперсія;
- внутрішньо групова дисперсія;  - загальна дисперсія.
- загальна дисперсія.
Чим Rближче до 1, тим тісніший зв'язок між ознаками.
Лінійний коефіцієнт кореляції використовують для вимірювання тісноти прямолінійних зв'язків.
Мірою тісноти зв'язку як лінійного, так і нелінійного є коефіцієнт детермінації R2 — співвідношення факторної і загальної дисперсії:

|
де (6.4)
Корінь квадратний з коефіцієнта детермінації є індекс кореляції R
У кореляційно-регресійному аналізі істотність зв'язку перевіряється так само, як і в аналітичному групуванні за допомогою R2 чи F-критерія:
 (6.5)
(6.5)
В основі кореляційно-регресійного аналізу лежить припущення, що залежність між факторною і результативною ознаками може бути виражена функцією У=f[х), яка називається рівнянням регресії.
Рівняння регресії— аналітичне рівняння, за допомогою якого можна виразити зв'язок між ознаками. Тобто це економіко-схематична модель залежності результативної ознаки від факторної. Графіком рівняння регресії є лінія регресії, яка описує кореляційний зв'язок. При побудові графіка значення факторної ознаки відкладаються на горизонтальній осі (ОХ), а результативної — на вертикальній (ОУ).
За аналітичним виразом залежність може бути лінійною і нелінійною. Найбільш поширені такі рівняння регресії:
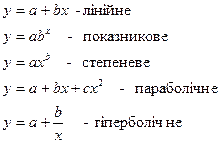
де Y — теоретичні значення результативної ознаки; а, b і с — параметри рівняння регресії, які називаються коефіцієнтами регресії.
На першому етапі кореляційно-регресійного аналізу при обґрунтуванні моделі, як і в аналітичному групуванні, розв'язуються два питання: вибір факторної і результативної ознаки та вибір виду рівняння регресії.
Правильний вибір ознак і виду рівняння регресії потребує теоретичного аналізу взаємозв'язку. Для підтвердження правильності вибору виду рівняння регресії часто застосовується графічне зображення зв'язку у вигляді кореляційного поля.При його побудові на осі абсцис треба відкласти значення факторної ознаки х, а на осі ординат — результативної ознаки у. Кожній одиниці сукупності на графіку відповідає окрема точка. За формою розміщення точок на кореляційному полі робиться висновок відносно виду регресійного рівняння. При великому обсязі сукупності доцільно на графіку зображати групові середні попередньо побудованого аналітичного групування. Лінію групових середніх називають емпіричною лінією регресії.
Для визначення виду рівняння регресії застосовується також спосіб перебору функцій, коли обчислюють рівняння регресії різних видів і з них на основі статистико-математичних критеріїв вибирають найкраще.
На етапі оцінки лінії регресії визначають параметри обраного рівняння методом найменших квадратів на основі побудови і розв'язку відповідної системи нормальних рівнянь. Лінійній функції відповідає система таких рівнянь з двома невідомими:
 (6.6)
(6.6)
Особливу увагу слід звернути на інтерпретацію параметрів лінійного рівняння регресії а і b. Параметр b показує на скільки одиниць власного виміру змінюється середнє значення результативної ознаки зі збільшенням факторної ознаки на одиницю власного вимірювання. Параметр а — теоретичне значення Y для х=0.
Типова задача:
За допомогою методу кореляційно – регресійного аналізу визначити наявність і характер зв'язку між віком устаткування і витратами на ремонт. За даними таблиці обчислимо параметри:
а0 =(27*536-217,1*70) / (10*536 – 70*70) = - 1,576
а1 =(10*217,1 - 27*70) / (10*536 – 70*70) = 0,611
Таким чином, зв'язок між віком устаткування і витратами на ремонт прямий. Лінійне рівняння регресії буде мати вид:
У= -1,576+0,611х.
Розрахуємо теоретичні значення Y підставивши значення х у рівняння регресії та запишемо їх в таблицю 6.1.
Таблиця 6.1.
Вік устаткування і витрати на ремонт по групі підприємств
| № п/п | Вік устатку- вання років, х | Витрати на ремонт тис.грн., у | 
| xy | Y | (yi-Yi)2 | 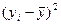
|
| 1,5 | 6,0 | 0,868 | 0,399 | 1,440 | |||
| 2,0 | 10,0 | 1,479 | 0,271 | 0,490 | |||
| 5 | 1,4 | 7,0 | 1,479 | 0,006 | 1,690 | ||
| 6 | 2,3 | 13,8 | 2,090 | 0,044 | 0,160 | ||
| 2,7 | 21,6 | 3,312 | 0,374 | 0,000 | |||
| 4,0 | 40,0 | 3,312 | 0,285 | 1,690 | |||
| 2,3 | 18,4 | 4,534 | 1,024 | 0,160 | |||
| 2,5 | 17,5 | 2,700 | 0,040 | 0,040 | |||
| 6,6 | 72,6 | 5,145 | 2,117 | 15,210 | |||
| 1,7 | 10,2 | 2,090 | 0,152 | 1,000 | |||
| Разом | 27,0 | 217,1 | 27,010 | 4,712 | 21,920 |
Залишкова дисперсія дорівнює:
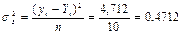
Загальна дисперсія:

Тоді факторна дисперсія розрахується на основі правила додавання дисперсій:
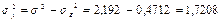
Коефіцієнт детермінації буде дорівнювати.
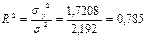
(або 78,5% загальної варіації витрат на ремонт залежить від віку устаткування).
Розрахуємо коефіцієнт кореляції:

Це значить, що між віком устаткування і витратами на ремонт існує прямий зв'язок.
Перевіримо істотність коефіцієнта кореляції за допомогою таблиці критичних значень. Для цього розрахуємо K1=m-1=2-1=1; K2=n-m=10-2=8. Коефіцієнт буде істотним, якщо він перевищить відповідне табличне значення. Перевіримо істотність коефіцієнта за допомогою F-критерія:

При α=0.01 F(1,8)=11.26. Це менше фактичного значення (54.6). Отже, коефіцієнт кореляції істотний і відбиває зв'язок між віком устаткування і витратами на ремонт.
Завдання для самостійної роботи:
1.Наведено дані про показники діяльності підприємств.:
Таблиця 6.2
Показники діяльності підприємств
| Номер підприємства | Вартість основних виробничих фондів, млн., грн | Дохід (виручка) від реалізації продукції (робіт, послуг), млн. грн |
1. Описати лінійний зв'язок між вартістю основних виробничих фондів та випуском продукції.
2. Оцінити щільність зв’язку між вартістю основних виробничих фондів та випуском валової продукції.
3. Перевірити істотність зв’язку.
2.У таблиці наведено банківські депозити по різних видах вкладів:
Таблиця 6.3
Банківські депозити по різних видах вкладів
| Вклади | Депозитні ставки, % | ||||||
| У гривнях | 15,1 | 12,8 | 13,8 | 14,1 | 12,1 | 10,1 | 14,5 |
| У валюті | 10,2 | 10,1 | 9,8 | 9,9 | 10,9 | - | - |
За наведеними даними:
1) складіть аналітичне групування;
2) обґрунтуйте наявність зв’язків між величиною депозитної ставки та видом вкладу;
3) обчисліть загальну та між групову дисперсії, а також групові та середню з групових дисперсій. Розкрийте їх взаємозв’язок;
4) використовуючи кореляційне відношення, оцініть щільність зв’язку між зазначеними ознаками, перевірте істотність зв’язку з імовірністю 0,95, зробіть висновки.
3.Затримка літаків в аеропорті через метеорологічні умови характеризується даними:
Таблиця 6.4
Показники затримки літаків в аеропорті
| Метеорологічні умови | Кількість літаків | Середній час затримки літаків, год |
| Несприятливі | ||
| Нестійкі | ||
| Сприятливі | ||
| У цілому | 3,8 |
Визначіть між групову та середню з групових дисперсій затримки літаків, коли відомо, що загальна дисперсія дорівнює 10. Оцініть щільність зв’язку та перевірте його на істотність з імовірністю 0,95.
Література: основна [1-4, 7]
додаткова [3, 7 -9]
Практична робота №7
Тема: Вибірковий метод
Мета практичної роботи:Закріпити на навчальних ситуаціях теоретичний матеріал за темою лекції “Вибірковий метод”.
Контрольні запитання:
1. Суть і переваги вибіркового спостереження.
2. Обчислення похибок вибірки й визначення меж інтервалу для середньої величини і частки.
3. Визначення необхідного обсягу вибірки.
4. Види вибірки і способи відбору, що забезпечують репрезентативність.
Практичні заняття з теми передбачають:
1. Визначити середнью помилку вибірки для середньої. Пояснити техніку
обчислення та економічний зміст.
2. Визначити середню помилку вибірки для долі. Пояснити техніку
обчислення та економічний зміст.
3. Визначити граничну помилку вибірки для середньої. Пояснити техніку
обчислення та економічний зміст.
4. Визначити граничну помилку вибірки для частки. Пояснити техніку
обчислення та економічний зміст.
5. Визначння необхідної чисельності вибірки. Доведення формули.
6. Способи розповсюдження результатів вибірки на генеральну сукупність.
Методичні вказівки до теми:
Вибірковим спостереженням —називається таке спостереження, при якому вся сукупність одиниць характеризується за деякою їх частиною, відібраною у випадковому порядку.
Характеристики вибіркової сукупності є оцінками відповідних параметрів генеральної сукупності. Але вибірка не точно відтворює генеральну сукупність, і тому оцінки не співпадають із самими параметрами.
Розбіжності між ними називаютьсяпомилками репрезентативності.
Вони бувають систематичними та випадковими.
Систематичні помилки виникають, коли при формуванні вибіркової сукупності не був дотриманий принцип випадковості відбору, який забезпечує всім елементам генеральної сукупності рівні можливості потрапити у вибірку. Систематичні помилки для всіх елементів сукупності мають односторонній напрям і тому їх називають помилками зміщення.
На відміну від них, помилки, які неминуче виникають і при додержанні принципу випадковості відбору, але не носять тенденційного характеру, мають назвувипадкових і не ведуть до зміщення оцінок.
Помилка вибірки обчислюється за формулами:
| Повторна вибірка | Безповторна вибірка |
Для середньої  (7.1) (7.1)
|  (7.2) (7.2)
|
Для частки 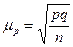 (7.3) (7.3)
|  (7.4) (7.4)
|
де  – середня помилка вибірки;
– середня помилка вибірки;
 – дисперсія;
– дисперсія;
n – число одиниць вибіркової сукупності;
N – число одиниць генеральної сукупності;
W – частка одиниць з однаковою ознакою у загальній чисельності одиниць вибірки.
Гранична помилка вибірки обчислюється за формулою:
 , (7.5)
, (7.5)
де t – коефіцієнт кратності помилки;
 – середня помилка вибірки.
– середня помилка вибірки.
Значення t при імовірності 0,683 дорівнює 1;
0,954 дорівнює 2;
0,997 дорівнює 3;
0,999 дорівнює 4.
Вищенаведені формули граничних помилок вибірки після відповідних перетворень можна використати для обчислення необхідної чисельності вибірки (п).
Формули для визначення необхідної чисельності вибірки:
| Повторна вибірка | Безповторна вибірка | |
| Для середньої |  (7.6) (7.6)
| 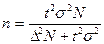 (7.7) (7.7)
|
| Для частки | 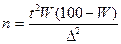 (7.8) (7.8)
| 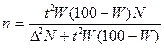 (7.9) (7.9)
|
Типові задачі:
1.Розглянемо методику вибіркового оцінювання середньої та частки за даними обстеження 100 зареєстрованих безробітних (2%-на вибірка), з яких 40 проходять перенавчання за новою професією. За результатами обстеження середня тривалість перерви в роботі становить 3 місяці, а дисперсія дорівнює 2,25.
Визначимо межі середньої тривалості перерви в роботі з імовірністю 0,954(t=2).
Гранична похибка 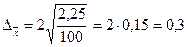 (міс).
(міс).
Довірчий інтервал : 3-0,3 
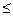 3+0,3.
3+0,3.
Це дає підставу стверджувати з імовірністю 0,954, що середня тривалість перерви в роботі становить не менш як 2,7 і не більш як 3,3 місяця.
Перш ніж визначати граничну похибку частки безробітних, які перенавчаються, обчислимо дисперсію частки:

Гранична похибка
 , або 9,8 %.
, або 9,8 %.
Довірчий інтервал: 30-9,8 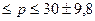 .
.
Отже, з такою самою ймовірністю можна стверджувати, що частка безробітних, які перенавчаються, у генеральній сукупності становить не менш як 20,2% і не більш як 39,8%.
Відносна похибка середньої тривалості перерви в роботі  %. Такий самий результат дістаємо, обчислюючи відносну похибку на основі коефіцієнта варіації:
%. Такий самий результат дістаємо, обчислюючи відносну похибку на основі коефіцієнта варіації: 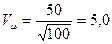 %, де
%, де  %.
%.
Відносна похибка частки безробітних, які перенавчаються, становить 8,1 %, що перевищує похибку для середньої тривалості перерви в роботі: 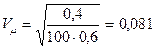 .
.
2.На лісовому масиві в 400 га визначається загальний запас деревини. Пробні ділянки мають площу по 0,1 га. За даними попередніх обстежень середнє квадратичне відхилення виходу деревини з 0,1 га становить 3 м3. Скільки пробних ділянок необхідно обстежити, щоб похибка вибірки з імовірністю 0,954 (для якої і = 2 ) не перевищувала 1 м3?
Достатній обсяг вибірки пробних ділянок 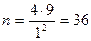 .
.
 3. Проектується вибіркове обстеження підприємстві малого бізнесу в галузі інформаційно-обчислювального обслуговування (N = 180) з метою визначення середньої тривалості обороту дебіторської заборгованості. За аналогічними обстеженнями в інших галузях діяльності середня тривалість обороту становить 65 днів, квадратичний коефіцієнт варіації V = 30 %.
3. Проектується вибіркове обстеження підприємстві малого бізнесу в галузі інформаційно-обчислювального обслуговування (N = 180) з метою визначення середньої тривалості обороту дебіторської заборгованості. За аналогічними обстеженнями в інших галузях діяльності середня тривалість обороту становить 65 днів, квадратичний коефіцієнт варіації V = 30 %.
Мінімально достатній обсяг вибірки, за якого з імовірністю 0,954 гарантується відносна похибка вибірки в обсязі не більш як 10%, становить 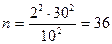 .Скоригуємо цей обсяг на без повторність вибірки:
.Скоригуємо цей обсяг на без повторність вибірки:  .
.
Завдання для самостійної роботи:
1.Для обчислення середнього процента природних втрат товару було проведено обстеження 100 – із 1640 рівних за вагою партій товару і одержано такі дані:
Таблиця 7.1.
Розподіл товару за процентом природних втрат
| Процент втрат | Кількість партій |
| 3-5 | |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| 11-13 | |
| Разом: |
Визначити з імовірністю 0,997 в яких знаходиться середній процент природних втрат в генеральній сукупності та з імовірністю 0,954 частку партій товару з природними втратами понад 9 %.
2.Для визначення середнього навантаження на одного продавця було обстежено 100 продавців. В результаті 10 % обстеження були одержані такі дані:
Таблиця 7.2
Розподіл продавців за розміром роздрібного товарообігу
| Товарообіг на 1 продавця, тис. грн. | Число продавців |
| 0-5 | |
| 5-10 | |
| 10-15 | |
| 15-20 | |
| Разом: |
Визначити:
1. Середнє навантаження на одного продавця.
2. Середнє квадратичне відхилення.
3. З імовірністю 0,954, в яких межах знаходиться середнє навантаження в генеральній сукупності та частку продавців з продуктивністю понад 10 тис. грн.
3.Вибірково обстежено 25 спеціалізованих відділів тканин. Встановлено, що в середньому на обслуговування одного покупця втрачається 23 хвилин при середньому квадратичному відхиленні 5 хвилин.
Визначити з імовірністю 0,954, в яких межах знаходяться затрати часу в генеральній сукупності.
4.Із 2000 спеціалізованих магазинів взуття потрібно відібрати певну кількість для визначення середнього числа покупців на один магазин. Помилка вибірки з імовірністю 0,954 не повинна перевищувати 5 чоловік, при середньому квадратичному відхиленні 20 чоловік.
Скільки необхідно відібрати магазинів для обстеження?
5.Перевірено 600 шт. готових виробів, з яких 10 шт. виявились бракованими. Визначити з імовірністю 0,954 граничну помилку вибірки при обчисленні частки бракованих виробів у всієї партії, яка налічує 10000 шт. готових виробів.
6.Проведено безповторну вибірку 400 електроламп з партії 2000 штук. Визначити з імовірністю 0,997 межі середньої тривалості горіння електроламп, якщо вибіркова середня дорівнює 1300 год., а вибіркове середнє відхилення 26,5 год.
Література: основна [2, 4, 7, 8]
додаткова [3, 4, 9]
Практична робота №8
Тема: Аналіз інтенсивності динаміки
Мета практичної роботи:Закріпити на навчальних ситуаціях теоретичний матеріал за темою лекції “Аналіз інтенсивності динаміки ”.
Контрольні запитання:
1. Суть і складові елементи динамічного ряду. Види рядів динаміки.
2. Статистичні характеристики динамічних рядів і їх взаємозв’язок.
3. Економічна суть і техніка розрахунку середніх значень основних
характеристик рядів динаміки.
Практичне заняття з теми передбачає:
1. Обчислення статистичних характеристик динамічних рядів та визначення їх взаємозв’язку.
2. Перетворення рядів динаміки шляхом укрупнення інтервалів та плинної середньої. Техніка перетворення.
3. Приведення рядів динаміки до однієї основи. Техніка приведення.
4. Інтерполяція та екстраполяція. Способи та техніка обчислення.
5. Змикання рядів динаміки. Техніка змикання.
6. Аналітичне вирівнювання ряду динаміки. Техніка вирівнювання.
Методичні вказівки до теми:
Рядом динаміки називається ряд чисел, що характеризують зміну величини суспільного явища в часі.
Розрізняють ряди динаміки абсолютних, відносних і середніх величин.
Ряди динаміки абсолютних величин бувають моментними і періодичними.
Кожний ряд динаміки можна охарактеризувати за допомогою таких показників: абсолютний приріст, коефіцієнт зростання, темп зростання, темп приросту, абсолютне значення одного процента приросту, середній рівень ряду динаміки, середній абсолютний приріст, середній темп зростання та приросту.
Абсолютний приріст обчислюється як різниця між поточним (звітним) і базисним рівнями.
| <== попередня сторінка | | | наступна сторінка ==> |
| Виконання практичних робіт здійснюється студентами самостійно під керівництвом викладача під час проведення аудиторних занять. | | | Базисний Ланцюговий |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |
