• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Поняття векторного простору, базису та координат вектора

Означення 3.4.1.Множину геометричних векторів будемо називати векторним простором, якщо лінійні операції над будь-якими векторами цієї множини, тобто додавання двох векторів і множення вектора на будь-яке число, дають вектори тієї ж множини.

Згідно з цим означенням множина всіх векторів, які паралельні деякій прямій, є векторним простором. Множина всіх векторів, які паралельні деякій площині, також є векторним простором.

Означення 3.4.2.Базисом (базою) векторного простору називається така упорядкована сукупність векторів цього простору, яка задовольняє умовам:

· ця сукупність векторів є лінійно незалежною;

· будь-який вектор простору може бути представлений у вигляді лінійної комбінації векторів зазначеної упорядкованої сукупності.

Примітка. На подальшому при поширенні поняття векторного простору буде показано, що будь-які дві різні бази векторного простору мають однакову кількість векторів. Внаслідок чого є коректним наступне означення.

Означення 3.4.3.Число векторів довільного базису простору називається вимірністю даного векторного простору.

Вимірність векторного простору, що містить всі можливі геометричні вектори, дорівнює трьом. За базис у ньому можна взяти упорядковану сукупність будь-яких трьох некомпланарних векторів. Дійсно, згідно з наслідком з теореми 3.3.3 ці вектори лінійно незалежні. А за теоремами 3.3.1 та 3.3.4 будь-який інший вектор простору може бути надано у вигляді лінійної комбінації векторів базису. Множина векторів, які паралельні деякій площині, є двовимірним векторним простором. Надалі будемо розглядати тільки тривимірний векторний простір.

Лема 3.4.1. Нехай вектори 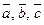утворюють базис тривимірного векторного простору, тоді будь-який вектор 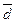простору є лінійною комбінацією базисних векторів: .

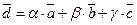4 За теоремою 3.3.4 чотири вектори 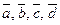– лінійно залежні, тобто 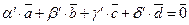і один з коефіцієнтів у цій рівності відмінний від нуля. Покажемо, що це саме коефіцієнт 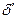при векторі .

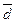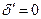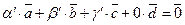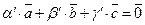Припустимо супротивне. Нехай . Тоді маємо або , причому один з коефіцієнтів у останній рівності – відмінний від нуля. Це суперечить факту лінійної незалежності базисних векторів. Таким чином, 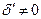, тоді 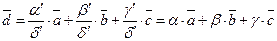.3

Означення 3.4.4.Числа 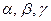у розкладі 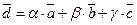вектора 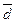за базисом 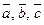називаються координатами вектора 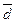у цьому базисі. При цьому коефіцієнт 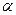при першому базисному векторі називається першою координатою, а коефіцієнти 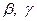при векторах 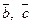– другою та третьою координатами вектора відповідно.

Умовимося вектор 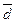, що має у базисі 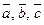координати 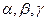, позначати так: .

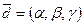Теорема 3.4.1. Координати вектора у заданому базисі єдині.

4Припустимо супротивне, що вектор 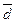має два різні набори координат у деякому базис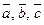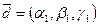і : і 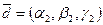. Тоді 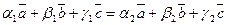. Звідки приходимо до рівності

,

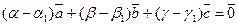у який принаймні один з коефіцієнтів при векторах 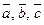відмінний від нуля. Але це означає, що базисні вектори 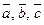лінійно залежні, що суперечить означенню базиса. Отже, припущення про те, що вектор 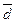у базисі 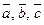може мати різні координати, є невірним. 3

Теорема 3.4.2. Будь-яка координата суми скінченного числа векторів дорівнює сумі відповідних координат доданків. При множенні вектора на число, його координати множаться на це число.

4 Нехай 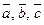– базис тривимірного векторного простору, а 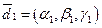, , 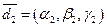…, 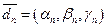– деякі вектори цього простору. За означенням координат вектору, маємо

.

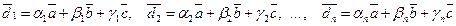Тоді

.

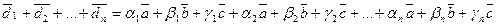За властивостями лінійних операцій над векторами можна переставляти місцями доданки у сумі та виносити за дужки спільний множник із групи доданків. У силу цього

.

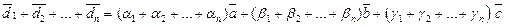Звідки виходить, що

,

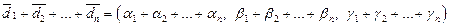тобто будь-яка координата суми векторів дорівнює сумі відповідних координат доданків.

Аналогічним образом доводиться, що 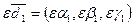.3

Переглядів: 2528