Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

Основні етапи:

а) відмітити точку М і побудувати пряму D₁М;

б) назвати площину бічної грані, якій належить пряма D₁М – площина АА₁D₁D;

в) назвати пряму, яка лежить у знайденій бічній грані і площині основи АВCD – пряма AD;

г) побудувати шукану точку – К, точку перетину прямих MD₁ і AD;

д) обчислити довжину відрізка КD₁:

KD₁=KM+MD₁.

За умовою задачі AA₁=2cм, а точка М – середина АА₁, тому

АМ=МА₁= = =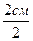1см.

Для знаходження довжини відрізка МD₁ розглянемо прямокутний трикутник МА₁D₁ (ÐA=90⁰). За теоремою Піфагора:

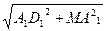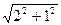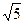МD₁= = = (см).

Для знаходження довжини відрізки КМ розглянемо інший прямокутний

трикутник КМА. DКМА = DМА₁D₁– за другою ознакою рівності трикутників:

ÐКАМ =ÐМА₁D₁ =90⁰; МА₁ =МА, так як точка М – середина АА₁ (за умовою);

ÐКМА=ÐА₁МD₁ – як вертикальні.

З рівності даних трикутників слідує рівність їх сторін.

Отже, КМ=MD₁= 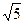см і КD₁ = 2MD₁ = 2 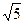см.

Відповідь: 2 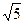см.

ЗАДАЧІ НА АКСІОМИ СТЕРЕОМЕТРІЇ.

1.Користуючись зображенням куба ABCDA₁B₁C₁D₁, вкажіть точки, які:

а) не належать передній грані;

б) належать верхній грані;

в) належать грані ABCD;

г) не належать грані A₁B₁ВА .

Рис.2

2.Користуючись зображенням куба ABCDA₁B₁C₁D₁ вкажіть:

а) спільні точки верхньої і передньої граней;
б) пряму перетину площин задньої і нижньої граней;

в) спільні точки площин граней ABВ₁A₁ і A₁B₁C₁D₁ ;

г) пряму перетину площин граней A₁B₁C₁D₁ і ВВ₁С₁С.

3.Користуючись зображенням куба АВСDA₁B₁C₁ D₁,

вкажіть, яку площину визначають прямі:

а) АВ і АD;

б) BC і CC₁;

в) DC і СС₁;

г) A₁B₁ і B₁A.

4.Користуючись зображенням куба ABCDA₁B₁C₁D₁, доведіть, що можна провести площину через прямі:

а) АС і СС₁;

б) AD і DC₁.

5. Щоб поверхня розпилу чотирикутної балки (рис.3) була плоскою, столяр зробив так: позначив на ребрі балки точку А і провів від неї в потрібному напрямі два відрізки АВ і АС у суміжних гранях балки, потім направив пилку по намічених відрізках . Поясніть, чому повинна утворитися плоска поверхня розпилу?

6.Точки А, В, С лежать у кожній з двох різних площин. Доведіть, що ці точки лежать на одній прямій.

7.Дано дві різні прямі, які перетинаються в точці А. Доведіть, що всі прямі, які перетинають обидві дані прямі й не проходять через

точку А, лежать в одній площині.

8.Дано чотири точки, що не лежать в одній площині. Скільки можна провести різних площин, які проходять через три з цих точок? Відповідь поясніть.

9.Доведіть, якщо вершини трикутника АВС належать деякій

площині a, то трикутник АВС лежить в цій площині.

10.Доведіть, що чотирикутник АВСD лежить в одній площині, якщо його діагоналі АС і BD перетинаються.

ЗАДАЧІ НА ПЕРЕРІЗИ.

1.Відрізки АВ і АС перетинають площину a. Чи перетинає її відрізок ВС? А пряма ВС?

2.Побудуйте переріз прямокутного паралелепіпеда АВСDA₁B₁C₁D₁ площиною, яка проходить через:

а) точки А, В₁ і D₁;

б) точки А, С і середину ребра DD₁.

3.Чи може бути перерізом куба рівнобедрений трикутник, правильний трикутник, прямокутник, квадрат, трапеція?

4.Доведіть що перерізом тетраедра не може бути п’ятикутник.

5.У трикутній піраміді SABC всі ребра дорівнюють 10 см. Побудуйте переріз піраміди площиною, яка проходить через ребро AS і точку М - середину ребра ВС. Знайдіть периметр побудованого перерізу.

6.Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через діагональ В₁D₁ верхньої основи і точку М – середину ребра АА₁. Обчисліть периметр перерізу, якщо ребро куба дорівнює 10 см.

7.Через середину трьох ребер куба, які виходять із однієї вершини, проведено переріз. Обчисліть периметр і площу перерізу, якщо ребро куба дорівнює 6 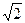см.

8.У трикутній піраміді, кожне ребро якої дорівнює 4 см, побудовано переріз площиною, яка проходить через середину трьох ребер, що виходять із однієї вершини. Обчисліть периметр і площу утвореного перерізу.

9.У кубі ABCDA₁B₁C₁D₁ точка М лежить на ребрі А₁В₁, причому

МВ₁ = 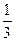А₁В₁. Побудуйте точку N перетину прямої АМ з площиною грані ВВ₁С₁С та знайдіть довжину відрізка MN, якщо ребро куба рівне 12 см.

10.Довжини трьох ребер прямокутного паралелепіпеда, що виходять з однієї вершини, дорівнюють 6 см, 6 см і 8 см. Побудуйте переріз паралелепіпеда площиною, яка проходить через середини ребер, і знайдіть його периметр.

ТЕМА 1.2.ПАРАЛЕЛЬНІСТЬ ПРЯМИХ І ПЛОЩИН.

<== попередня сторінка	\|	наступна сторінка ==>
Задача №3.	\|	Анотація

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.