Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЛЕКЦІЯ 25

8.5. Фільтрація сигналів із шумів (може виноситися на самоопрацювання)

Визначальна відмінність задачі фільтрації від інших задач теорії оптимального прийому полягає в тому, що передане повідомлення (інформаційний параметр ), яке невідоме одержувачу, являє собою випадковий процес. У всіх інших задачах інформаційний параметр являє собою випадкову величину. Тому вичерпне розв'язання задачі фільтрації полягає в тому, що для параметра при кожному поточному значенні часу необхідно обчислювати його апостеріорну щільність ймовірності .

У переважній більшості практичних додатків фільтрації використовується не щільність ймовірності, а оцінка параметра , що є в деякому змісті найкращою (наприклад, оцінка по максимуму апостеріорної щільності ймовірності). Однак у загальному випадку відшукання оцінок вимагає попередньої побудови щільності ймовірності, тому останнє завдання займає в теорії фільтрації центральне місце.

Для фільтрації характерна наступна постановка задачі. Нехай у місці приймання, починаючи з моменту , спостерігається реалізація процесу

, (53)

де корисне повідомлення, що представляє собою реалізацію випадкового процесу з відомими статистичними властивостями; сигнал, що є безперервною функцією й часу ; нормальний білий шум з нульовим середнім і спектральною щільністю .

Потрібно знайти оцінку ,що у деякому сенсі була б найкращою стосовно переданого повідомлення . Надалі реалізацію , що спостерігається в поточному часі ,будемо позначати .

Сформульована задача може вирішуватися в більш загальній постановці, коли оцінка будується на інтервалі часу, що не збігається з інтервалом спостереження: при спостереженнях відшукується оцінка , причому при маємо задачу фільтрації в поточному часі; при задачу фільтрації з попередженням (задачу екстраполяції); при задачу фільтрації із запізнюванням (задачу інтерполяції).

Фільтрація в поточному часі характерна для таких додатків, як радіозв'язок, радіолокація, радіонавігація або телебачення. Задача фільтрації в інших постановках виникає, наприклад, у задачах розвідки або наукового експерименту.

Задача фільтрації в поточному часі займає також суттєве місце в багатьох процедурах автоматичного управління. Так, призначення важливого класу автоматичних систем, що стежать, полягає в тому, щоб вони з можливо більшою точністю повторювали рух, що задається деяким випадковим процесом, який спостерігається на фоні шуму. Тому далі основна увага приділяється розв'язанню задачі фільтрації в поточному часі.

Як і в інших задачах теорії оптимального прийому сигналів, при знаходженні оцінок використовуються не тільки результати спостереження, але й попередні (апріорні) відомості про передані повідомлення.

Більшість з реальних безперервних повідомлень апріорно можна описати випадковим процесом , що визначається диференціальним рівнянням

, (54)

де нормальний випадковий процес із нульовим математичним сподіванням і функцією кореляції .

Процес при цьому можна трактувати як результат проходження нормального білого шуму через інтегруючий ланцюг з параметрами .

Лінійний ланцюг, що формує передане повідомлення з нормального білого шуму, називається формуючим фільтром, а шум інформаційним шумом. Оскільки лінійні перетворення не змінюють властивості нормальності, то сформований процес , як і , є нормальним.

Постійна має сенс ширини енергетичного спектра процесу на рівні 0,5 від його максимального значення, а зміст величини, що характеризує тривалість перехідних процесів у формуючому фільтрі. Щоб рівняння (54) правильно відображало характер переданого повідомлення, необхідно задавати відповідне значення спектральної щільності шуму . Відомо, що дисперсія процесу, обумовленого рівнянням (54), дорівнює . Тому

, (55)

де дисперсія переданого повідомлення .

У цей час у зв'язку із широким впровадженням у практику обробки інформації цифрової техніки виникає необхідність опису випадкових процесів у дискретному часі. Здійснимо в рівнянні (54) перехід від безперервного часу до дискретного. Відліки дискретного часу,де будемо здійснювати через рівні інтервали .

Приймаючи значення процесу 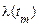за початкове, знайдемо значення , де . Для цього проінтегруємо (54) відповідно до відомих правил

Результат можна переписати у вигляді

, (56)

, , .

Значення отримані шляхом інтегрування некорельованого нормального шуму на непересічних відрізках, тому вони утворюють послідовність незалежних випадкових величин, що називається дискретним білим шумом. Кожна з випадкових величин має, як і вихідний шум , нормальний розподіл і нульове математичне сподівання. Знайдемо дисперсію значень .З огляду на те, що при нульовому математичному сподіванні центровані й істинні значення випадкових величин збігаються, отримаємо

. (57)

Якщо врахувати, що у випадку білого шуму , з (16.57) маємо

. (58)

Формула (58) показує, що дисперсія дискретного білого шуму , на відміну від безперервного аналога,обмежена.

При досить малих значеннях інтервалів можна вважати

. (59)

Отримане вище рівняння (56) є рівнянням у кінцевих різницях. Різницеві рівняння мають більшу спільність у порівнянні з диференціальними рівняннями. Існують процеси, які можна описати різницевими рівняннями й не можна диференціальними, хоча всяке диференціальне рівняння можна звести до різницевого рівняння.

Процес формування повідомлення з дискретного білого шуму, згідно (56) можна інтерпретувати за допомогою схеми (рис. 2), що є дискретним аналогом інтегруючого фільтра .

Рис. 2. Дискретний аналог інтегруючого фільтра

Рівняння спостереження (53) у дискретному часі має вигляд:

, (60)

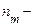де спостереження в момент часу , передане повідомлення, корисний сигнал, шум, що представляє собою послідовність незалежних випадкових величин, які мають нормальний розподіл з нульовим середнім і дисперсією .

Як критерії оптимальності при фільтрації в поточному часі зазвичай використовуються так звані точкові критерії й оцінки, які характеризуються тим, що вхідні в них величини належать тільки до одного розглянутого моменту часу .

Нехай деяка оцінка, яка побудована для моменту . Вона, мабуть, буде випадковою по двох причинах. По-перше, через те, що випадковими є повідомлення . По-друге, у спостереження входить випадковий шум. Однак за критерій точності доцільно прийняти невипадкову величину, наприклад, мінімум середнього квадрата похибки

. (61)

Розглядаючи випадок дискретного часу, перепишемо (16.61) у такий спосіб

, (62)

де спільний розподіл і . Вираз (62) можна записати у вигляді

. (63)

Оскільки зовнішнє усереднення в (63) здійснюється по безумовному розподілу спостережень ,які містять незалежний шум, то мінімум досягається мінімізацією одного тільки внутрішнього інтеграла . З умови отримуємо

. (64)

Таким чином, оцінкою, оптимальною по мінімуму середнього квадрата похибки, є умовне математичне сподівання , що представляє собою апостеріорне середнє. Відповідно до (63)

, (65)

де дисперсія апостеріорного розподілу.

Нехай потрібно здійснювати фільтрацію процесу, заданого лінійним різницевим рівнянням першого порядку

, (66)

де послідовність незалежних гауссівських випадкових величин з нульовим математичним сподіванням і дисперсією .

Початкове значення будемо вважати нормальною випадковою величиною. Тоді всі наступні значення теж будуть нормальними, тому що вони утворюються за рахунок послідовних лінійних перетворень нормальних випадкових величин. Рівняння (66) має більшу спільність ніж рівняння (56), оскільки тут коефіцієнт і дисперсія шуму є функціями часу.

Нехай на вході приймального пристрою в момент спостерігається суміш сигналу із шумом

, (67)

де спостереження в момент часу , відома функція часу, передане повідомлення, 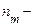шум, що представляє собою послідовність незалежних випадкових величин, що мають нормальний розподіл з нульовим середнім і дисперсією .

Добуток 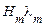є частковим випадком сигналу в рівнянні (60). При маємо, зокрема, задачу фільтрації огинаючої АМ коливання. За допомогою співмножника можуть бути враховані різні лінійні перетворення повідомлення, наприклад, зміна рівня сигналу при маневруванні приймача щодо передавача, коли вони встановлені на рухомих об'єктах. Оскільки рівняння (66), (67) є лінійними, процедура фільтрації у викладеній постановці називається лінійною фільтрацією.

Нехай є послідовність спостережень . Передбачаючи надалі скористуватися методом математичної індукції, припустимо, що апостеріорна щільність для моменту часу вже знайдена й опинилася нормальною. Знайдемо щільність і покажемо, що вона теж буде нормальною. Вираз для апостеріорного середнього визначить алгоритм формування оцінки, оптимальної за критерієм мінімуму середньої квадратичної погрішності, а апостеріорна дисперсія – точність цієї оцінки. Оскільки при нормальному розподілі найбільш ймовірне значення випадкової величини і її математичне сподівання збігаються, то отримана оцінка одночасно буде оптимальною за критерієм максимуму апостеріорної ймовірності.

Розглянемо вираз для щільності .На підставі теореми множення ймовірностей можна написати

. (68)

Величина при фіксованому значенні залежить тільки від і, отже, не залежить від ( і попередні значення шуму є незалежними за умовою задачи). Тому

. (69)

Крім того, сукупність , є , тому

. (70)

Отже, вираз (68) можна переписати у вигляді

. (71)

Співвідношення (71) являє собою один з варіантів формули гіпотез (Байєса). Співмножник не містить значень , тому йогоможна включити в нормувальну постійну щільності . Щільність можна знайти по формулі

. (72)

За припущенням щільність є нормальною

, (73)

де 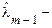математичне сподівання (апостеріорне середнє), а апостеріорна дисперсія на кроці .

Перехідна щільність ймовірності визначається з рівняння (66), відповідно до якого значення при фіксованому значенні являє собою суму невипадкового доданка й нормального шуму , що має нульове середнє й дисперсію . Тому

. (74)

Здійснюючи інтегрування в (72), знайдемо

. (75)

Нарешті, відповідно до рівняння (67)

. (76)

Тепер формулу (71) можна представити у вигляді

. (77)

Оскільки аргумент експонентної функції в (77) є поліномом другого ступеня відносно , то щільність є нормальною. Відповідно до методу математичної індукції вона буде нормальною при будь-якому т,тому що початковий розподіл був нормальним.

Параметри нормального розподілу (77) простіше визначити, якщо стандартний вираз нормальної щільності ймовірності представити у вигляді

. (78)

Згідно з (78) є коефіцієнтом при ( ), а коефіцієнтом при . Керуючись цим, з (77) отримаємо

. (79)

Випишемо з (77) вираз для коефіцієнта при й перетворимо його

. (80)

Рівняння (80) визначає алгоритм формування оптимальної оцінки, а рівняння (79) – еволюцію апостеріорної дисперсії. Рівняння (79) і (80) відомі як рівняння фільтра Калмана (рис. 3).

Рис. 3. Фільтр Калмана

Через у схемі фільтра позначена величина

. (81)

У рівняння дисперсії (79) входять тільки відомі функції часу, воно не містить спостереження , щовключає шум. Тому рівняння (79) може бути вирішене заздалегідь, до початку роботи фільтра, внаслідок чого функцію й коефіцієнт варто вважати відомими функціями часу.

Припустимо, що спостереження відсутні ( ). У цьому випадку апостеріорний розподіл збігається з апріорним розподілом, а з (80) одержуємо

. (82)

Рівняння (82) є рівнянням прогнозу за апріорним даними. Фільтр Калмана вироджується в цьому випадку у фільтр, виділений на схемі (рис. 3) пунктиром. Неважко помітити, що це є формуючий фільтр для прийнятого повідомлення (66). Таким чином, апріорні відомості про прийняті повідомлення «закладені в конструкцію» оптимального фільтра. На вході фільтра Калмана ізсигналу відраховується його передбачувана частина . Після цього зі спостережень із ваговим коефіцієнтом і з апріорних відомостей формується оптимальна оцінка . Процедура утворення оцінки є рекурентною, зручною для реалізації на елементах сучасної цифрової техніки.

Фільтр (80) є нестаціонарним (зі змінними в часі параметрами), причому нестаціонарність зберігається навіть при постійних значеннях величин . Ця обставина пов'язана із процесом установлення дисперсії . У тих випадках, коли постійні й існує межа , оцінка формується відповідно до

. (83)

Оцінка (83), загалом кажучи, не буде оптимальною. При 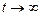має місце її асимптотична оптимальність. Фільтр із постійними параметрами, що відповідає алгоритму (83), називається стаціонарним. На практиці його реалізація значно простіше реалізації нестаціонарного фільтра (80).

Рівняння оптимальної лінійної фільтрації для безперервного часу виходять із рівнянь (79), (80) при й мають вигляд:

, (84)

, (85)

де , спектральна інтенсивність білого шуму на вході фільтра, що формує повідомлення.

Задача фільтрації називається нелінійною, якщо диференціальне рівняння, яким описується повідомлення, або рівняння спостереження є нелінійними. Другий випадок характерний для багатьох радіотехнічних додатків. Наприклад, у системах зв'язку з фазовою модуляцією математична модель сигналу на вході приймального пристрою має вигляд

де традиційно: амплітуда, несуча частота радіосигналу; корисне повідомлення; постійна, що має зміст індексу модуляції; шум.

Еволюція апостеріорної щільності ймовірності в задачах нелінійної фільтрації описується інтегродиференціальним рівнянням, яке не має загальних методів розв'язання. Системи рівнянь для моментних функцій апостеріорного розподілу в цьому випадку є незамкнутими, оскільки в рівняння для нижчих моментів входять вищі моменти. Тому задачі нелінійної фільтрації розв'язуються різними наближеними методами.

Один з наближених методів одержання оцінок повідомлення заснований на розкладанні нелінійної функції в статечний ряд за приростами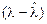

. (86)

Якщо в (86) обмежитися тільки наведеними лінійними членами, то задача нелінійної фільтрації зводиться до розглянутої раніше задачі лінійної фільтрації. Отримана в результаті використання такого прийому оцінка буде квазіоптимальною.

<== попередня сторінка	\|	наступна сторінка ==>
Кореляційний прийом випадкових сигналів	\|	Раздел II

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.015 сек.