
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування.
Система має один ступінь вільності, рівновага – стійка. На систему діють тільки потенціальні сили (сили ваги і пружна сила). Виведемо систему із стану рівноваги. Виберемо за узагальнену координату кут 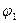 відхилення стержня 1 від вертикалі, вважаючи його малим (рис.Д7.б). Тобто маємо
відхилення стержня 1 від вертикалі, вважаючи його малим (рис.Д7.б). Тобто маємо 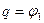 і
і 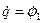 . Запишемо рівняння Лагранжа II роду:
. Запишемо рівняння Лагранжа II роду:
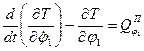 (7.1)
(7.1)
Визначимо кінетичну енергію системи, як суму енергій тіл системи. Враховуючи, що стержень 1 обертається навколо нерухомої осі 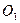 , диск 2 - навколо нерухомої осі
, диск 2 - навколо нерухомої осі 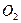 , а тіло 3 - рухається поступально, маємо:
, а тіло 3 - рухається поступально, маємо:
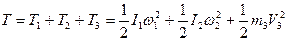 , (7.2)
, (7.2)
де моменти інерції однорідного стержня 1 довжиною 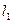 і шківа 2 (маса розподілена на ободі) відповідно дорівнюють:
і шківа 2 (маса розподілена на ободі) відповідно дорівнюють:
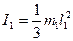 ,
, 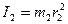 (7.3)
(7.3)
Виразимо швидкості, що входять в (7.2) через узагальнену швидкість 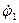 :
:
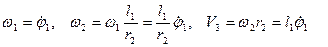 (7.4)
(7.4)
Підставимо (7.3) і (7.4) у вираз (7.2):
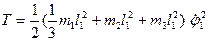 (7.5)
(7.5)
Кінетична енергія залежить тільки від узагальненої швидкості 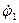 . Визначимо похідні, що входять в ліву частину рівняння (7.1):
. Визначимо похідні, що входять в ліву частину рівняння (7.1):
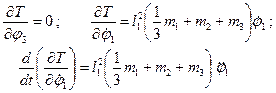 (7.6)
(7.6)
2. Визначимо узагальнену потенціальну силу, яка відповідає узагальненій координаті 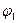 , за формулою:
, за формулою:
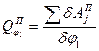 (7.7)
(7.7)
Зобразимо діючі на систему сили 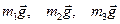 та
та 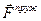 . Задамо системі можливе переміщення, при якому узагальнена координата
. Задамо системі можливе переміщення, при якому узагальнена координата 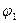 зростає, тобто
зростає, тобто 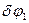 >0 , та покажемо можливі переміщення кожного з тіл: для тіла 2 – поворот на кут
>0 , та покажемо можливі переміщення кожного з тіл: для тіла 2 – поворот на кут 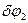 , для вантажу 3 – переміщення
, для вантажу 3 – переміщення 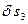 . Для визначення узагальненої потенціальної сили обчислимо суму можливих робіт сил на цьому можливому переміщенні системи:
. Для визначення узагальненої потенціальної сили обчислимо суму можливих робіт сил на цьому можливому переміщенні системи:
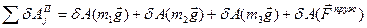 (7.8)
(7.8)
Можливу роботу сили ваги 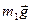 замінимо можливою роботою моменту сили ваги відносно точки О1, тобто:
замінимо можливою роботою моменту сили ваги відносно точки О1, тобто:
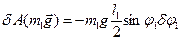 ,
,
бо плече між лінією дії сили 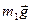 і точкою
і точкою 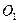 дорівнює
дорівнює 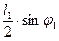 .
.
Для сил 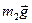 і
і 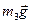 відповідно маємо:
відповідно маємо:
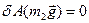 , бо точка прикладення сили
, бо точка прикладення сили 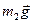 нерухома;
нерухома;
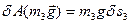 , бо кут між силою
, бо кут між силою 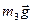 і
і 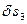 дорівнює нулю.
дорівнює нулю.
Можливу роботу пружної сили 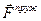 замінимо можливою роботою моменту пружної сили відносно точки О1, тобто
замінимо можливою роботою моменту пружної сили відносно точки О1, тобто
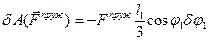 , бо плече між лінією дії сили
, бо плече між лінією дії сили 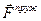 і точкою
і точкою 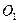 дорівнює
дорівнює 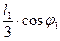 .
.
Величина пружної сили залежить від деформації пружини:
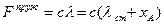 ,
,
де 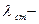 статична деформація пружини (в положенні рівноваги),
статична деформація пружини (в положенні рівноваги), 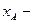 деформація пружини, коли систему вивели із стану рівноваги.
деформація пружини, коли систему вивели із стану рівноваги.
Враховуючи (7.4), виразимо можливе переміщення вантажу через узагальнене можливе переміщення 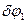 , а деформацію
, а деформацію 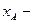 через узагальнену координату
через узагальнену координату 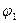 :
:
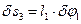 ;
; 
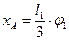 (7.9)
(7.9)
Підставимо (7.8) і (7.9) в формулу (7.7) та отримаємо узагальнену потенціальну силу у вигляді:
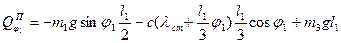 (7.10)
(7.10)
Коливання малі, тому можна вважати 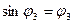 ,
, 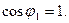 Розкриємо дужки і будемо мати:
Розкриємо дужки і будемо мати:
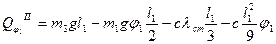 (7.11)
(7.11)
В положенні рівноваги (при 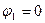 ) узагальнена потенціальна сила
) узагальнена потенціальна сила 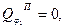 тобто:
тобто:
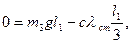 (7.12)
(7.12)
звідси знайдемо статичну деформацію 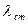 :
:
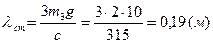
Таким чином, узагальнена потенціальна сила, враховуючи (7.12), остаточно буде мати вигляд:
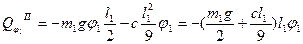 (7.13)
(7.13)
3. Складемо рівняння Лагранжа II роду. Підставимо (7.6) і (7.13) в рівняння (7.1):
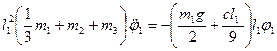 (7.14)
(7.14)
Запишемо диференціальне рівняння малих вільних коливань у вигляді :
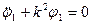 , тобто
, тобто  (7.15)
(7.15)
Підставимо числові значення, та знайдемо:
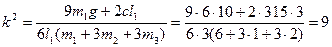 ,
,
звідки кругова частота малих вільних коливань 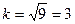 (с-1),
(с-1),
а період коливань 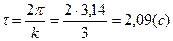
Відповідь: 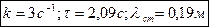 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад Д-7.1 | | | Примітка. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |