
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Завдання 1.
Контрольна робота
З теорії ймовірностей
Варіант 9
Завдання 1.
Два стрільці зробили по одному пострілу по мішені. Ймовірність попасти в мішень при одному пострілі для першого стрільця дорівнює 0,8, для другого – 0,9. Яка ймовірність, що попаде лише один стрілець?
Розв'язок
Позначимо події: А1 – перший стрілець попав у мішень; А2 – другий стрілець попав у мішень. Тоді протилежні події Ā1, Ā2 означають, що відповідний стрілець не попав у мішень.
Попадання лише одного стрільця у мішень означає, що або перший стрілець попав, а другий не попав, або другий стрілець попав, а перший не попав. Позначимо подію, що в мішень попав лише один стрілець, В. Тоді за формулою складання та множення ймовірностей маємо:
Р (В) = Р (А1) • Р (Ā2) + Р (А2) • Р (Ā1)
За умовою задачі, Р (А1) = 0,8; Р (А2) = 0,9. За правилом визначення імовірності протилежних подій, маємо:
Р (Ā1) = 1 – Р (А1) = 1 – 0,8 = 0,2
Р (Ā2) = 1 – Р (А2) = 1 – 0,9 = 0,1
Отже, ймовірність того, що у мішень попаде лише один стрілець, дорівнює:
Р (В) = 0,8 • 0,1 + 0,9 • 0,2 = 0,08 + 0,18 = 0,26
Завдання 2.
В ящику міститься 12 деталей, виготовлених на заводі № 1 і 20 деталей, виготовлених на заводі № 2. Імовірність того, що деталь, виготовлена на заводі № 1 стандартна, дорівнює 0,8, для деталей, виготовлених на заводі № 2, ця ймовірність дорівнює 0,7. Яка імовірність, що взята навмання деталь стандартна?
Розв'язок
Нехай подія А означає, що взята навмання деталь стандартна. Позначимо події: Н1 – деталь виготовлена на заводі № 1, Н2 – деталь виготовлена на заводі № 2. Позначимо умовні імовірності РН1(А), РН2(А) – деталь є стандартною при умові, що вона виготовлена відповідно на заводі
№ 1 та № 2. За умовою задачі, ці імовірності дорівнюють: РН1(А) = 0,8; РН2(А) = 0,7
Визначаємо імовірності подій Н1 та Н2:
12 12
Р(Н1) = –––––– = –––– = 0,375;
12 + 20 32
20 20
Р(Н2) = –––––– = –––– = 0,625;
12 + 20 32
За формулою повної імовірності визначаємо імовірність того, що взята навмання деталь є стандартною:
Р (А ) = РН1(А) • Р(Н1) + РН2(А) • Р(Н2) = 0,8 • 0,375 + 0,7 • 0,625 =
= 0,3 + 0,4375 = 0,7375.
Завдання 3.
Проведено n = 900 незалежних випробувань, в кожному з яких може відбутись подія А з імовірністю р = 0,8.
а) За локальною теоремою Муавра – Лапласа знайти імовірність того, що подія А наступить 709 раз.
б) За інтегральною теоремою Муавра – Лапласа знайти імовірність того, що подія А наступить від 700 до 729 раз.
Розв'язок
а) За локальною теоремою Муаврв – Лапласа, ймовірность того, що у n незалежних випробуваннях подія А відбудеться m разів визначається за формулою:
1 m – nр

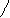




 Рn (m) = –––––––– • φ ( ––––––– )
Рn (m) = –––––––– • φ ( ––––––– )
npq npq
де р – імовірність того, що подія А відбудеться у кожному окремому незалежному випробуванні
q = 1 – р - імовірність того, що подія А не відбудеться у кожному окремому незалежному випробуванні
1
φ  (х) = ––––– • ( е – t²/ 2 ) –функція Гаусса
(х) = ––––– • ( е – t²/ 2 ) –функція Гаусса
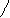
 2 π
2 π
m – nр

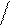 х = –––––––
х = ––––––– 
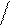
 npq
npq
Визначаємо х :
709 – 900 · 0,8 709 – 720 – 11


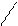
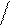 х = ––––––
х = –––––– 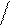 ––––––– = –––––––– = –––––– = – 0,92
––––––– = –––––––– = –––––– = – 0,92

 900 ·0,8 ·0,2 144 12
900 ·0,8 ·0,2 144 12
За таблицею значень функції Гаусса і враховуючи парність функції, визначаємо, що φ (– 0,92) = 0,2613
Звідси, ймовірність того, що що подія А наступить m = 709 раз, становить:
1 1


 Р900 (709) = –––––––– • φ ( – 0,92 ) = –––– • 0,2613 = 0,0218
Р900 (709) = –––––––– • φ ( – 0,92 ) = –––– • 0,2613 = 0,0218
144 12
б) За інтегральною теоремою Муавра-Лапласа, ймовірность того, що у n незалежних випробуваннях подія А відбудеться від m1 до m2 разів визначається за формулою:
m2 – nр m1 – nр
Рn (m1 ≤ m ≤ m2) = Ф ( ––––––– ) – Ф ( ––––––– )

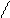


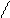
 npq
npq 
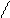
 npq
npq
де р – імовірність того, що подія А відбудеться у кожному окремому незалежному випробуванні
q = 1 – р - імовірність того, що подія А не відбудеться у кожному окремому незалежному випробуванні
1 х
 Ф (х) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
Ф (х) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
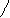
 2 π 0
2 π 0
m1 – nр m2 – nр



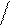 х1 = –––––––;
х1 = –––––––; 
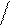 х2 = –––––––;
х2 = –––––––;

 npq npq
npq npq
Визначаємо х1 та х2 :
700 – 900 · 0,8 700 – 720 – 20

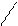

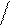 х1 = ––––––
х1 = –––––– 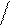 ––––––– = –––––––––– = –––––– = – 1,67
––––––– = –––––––––– = –––––– = – 1,67

 900 ·0,8 ·0,2 144 12
900 ·0,8 ·0,2 144 12
729 – 900 · 0,8 729 – 720 9




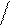 х2 = ––––––
х2 = –––––– 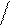 ––––––– = ––––––––– = ––– = 0,75
––––––– = ––––––––– = ––– = 0,75
 900 ·0,8 ·0,2 144 12
900 ·0,8 ·0,2 144 12
За таблицею значень функції Лапласа і враховуючи непарність функції, визначаємо, що Ф (– 1,67) = – 0,4526; Ф (0,75) = 0,2735.
Звідси, ймовірність того, що не подія А наступить від m1 = 700
до m2 = 729 раз становить:
Р900 (700 ≤ m ≤ 729) = Ф (0,75) – Ф (– 1,67) = 0,2735 + 0,4526 = 0,7261
Завдання 4 .
Дискретна випадкова величина задана рядом розподілу. Знайти функцію розподілу і побудувати її графік. Знайти математичне сподівання і дисперсію випадкової величини.
| х | |||
| р | 0,1 | 0,8 | 0,1 |
Розв'язок
Знаходимо функцію розподілу за формулою:
F = Р (Х < х )
де Р (Х < х ) – імовірність того, що випадкова величина Х прийме значення, менше за х.
При Х ≤ 1 F = Р (Х < 1) = 0
При 1 ≤ Х ≤ 2 F = Р (Х < 2) = Р (Х = 1) = 0,1
При 2 ≤ Х ≤ 4 F = Р (Х < 4) = Р (Х = 1) + Р (Х = 2) = 0,1 + 0,8 = 0,9
При Х > 4 F = Р (Х ≤ 4) = 1
Отже, функція розподілу має вигляд:
 0, Х ≤ – 1
0, Х ≤ – 1
 F (Х) = 0,1, 1 < Х ≤ 2
F (Х) = 0,1, 1 < Х ≤ 2
 0,9, 2 < Х ≤ 4
0,9, 2 < Х ≤ 4
1, Х > 4
Будуємо графік.
 F (Х)
F (Х)
 |


 1
1


 0,9
0,9

 0,1
0,1






 Х
Х
0 1 2 3 4
Обчислюємо математичне сподівання М(х):
М(х) = ∑х р = 1 ·0,1 + 2 ·0,8 + 4 ·0,1 = 0,1 + 1,6 + 0,4 = 2,1
б) обчислюємо дисперсію D (х):
D (х) = М(х2) – [М(х)] 2 = ∑х2 р– [М(х)] 2 = 12 ·0,1 + 22 ·0,8 + 42 ·0,1 – (2,1) 2 =
= 0,1 + 3,2 + 1,6 – 4,41 = 0,49
Завдання 5.
Випадкова величина Х задана функцією розподілу F(Х). Знайти щільність розподілу f (Х), імовірність попадання випадкової величини в інтервал (α, β). Побудувати графіки функцій F(Х) та f(х).
 0, Х ≤ 0
0, Х ≤ 0
 F (Х) = 2 sin х, 0 < Х ≤ π/6 α = 0, β = π/6
F (Х) = 2 sin х, 0 < Х ≤ π/6 α = 0, β = π/6
 1, Х > π/6
1, Х > π/6
Розв'язок
Знаходимо щільність розподілу за формулою:
f(х) = F ' (Х)
де F ' (Х) – перша похідна функції F(Х) в точці Х = х.
Знаходимо відповідні похідні.
При Х ≤ 0 F ' (Х) = 0 ' = 0
При 0 < Х ≤ π/6 F ' (Х) = (2 sin х) ' = 2 cos х
При Х > π/6 F ' (Х) = 1' = 0
Отже. функція щільності розподілу має вигляд:
 0, Х ≤ 0
0, Х ≤ 0
 f (Х) = 2 cos х, 0 < Х ≤ π/6
f (Х) = 2 cos х, 0 < Х ≤ π/6
 0, Х > π/6
0, Х > π/6
Знаходимо імовірність попадання випадкової величини Х в інтервал
(α = 0, β = π/6 ) за формулою:
Р (α < Х < β) = F (β ) – F (α)
де F (α) – значення функції F(Х) в точці Х = α,
F (β ) – значення функції F(Х) в точці Х = β
Р (0 < Х < π/6) = F (π/6 ) – F (0) = 2 sin π/6 – 0 = 2 · 0.5 = 1,0
Будуємо графіки.
Графік функції F(Х):

 F (Х)
F (Х)


 1,0
1,0



0 π/6 Х
Графік функції f(Х):
 f (Х)
f (Х)
 |
 2
2



 3
3





 Х
Х
0 π/6
Завдання6.
Випадкова величина Х задана щільністю розподілу f(Х). Знайти математичне сподівання і дисперсію випадкової величини Х. Знайти закон розподілу
х
F (Х) = ∫ f (х) d (х).
- ∞
Побудувати графіки функцій f(х) та F(Х).
 0, Х ≤ 3
0, Х ≤ 3
 f (Х) = 2 (х – 3) 3 < Х ≤ 4
f (Х) = 2 (х – 3) 3 < Х ≤ 4
 0, Х > 4
0, Х > 4
Розв'язок
Знаходимо математичне сподівання М (Х):
∞ 4 4
М (Х) = ∫ х·f (х) d (х) = ∫ х ·2 (х – 3) d (х) = 2 ∫ (х2 – 3х) d (х) =
- ∞ 3 3
 х3 3 х2 4 43 3·42 33 3·32
х3 3 х2 4 43 3·42 33 3·32
= 2 ·(––– – ––––) = 2 ( –– – ––– – ––– + ––– ) =
3 2 3 3 2 3 2
64 27 128 – 144 – 54 + 81 11 11
= 2 ( ––– – 24 – 9 + ––– ) = 2 ( ––––––––––––––––––– ) = 2 · –– = –––
3 2 6 6 3
Знаходимо дисперсію D (х):
∞ 4 11 2
D (Х) = ∫ х2·f (х) d (х) – [М(х)] 2 = ∫ х2 ·2 (х – 3) d (х) – (––– ) =
- ∞ 3 3
 4 121 х4 3х3 4 121
4 121 х4 3х3 4 121
= 2 ∫ (х3– 3х2) d (х) – ––– = 2·( ––– – ––––) – ––– =
3 9 4 3 3 9
 44 3·43 34 3·33 4 121 81 121
44 3·43 34 3·33 4 121 81 121
= 2 ( ––– – ––– – ––– + –––) – ––– = 2 ( 64 – 64 – ––– + 27) – ––– =
4 3 4 3 3 9 4 9
81 121 – 729 + 972 – 242 1
= 0 – ––– + 54 – –––– = ––––––––––––––– = –––
2 9 18 18
х
Знаходимо закон розподілу F (Х) = ∫ f (х) d (х).
- ∞
х
При Х ≤ 3 F (Х) = ∫ 0 d (х) = 0
- ∞
 3 х Х2 х
3 х Х2 х
При 3 < Х ≤ 4 F (Х) = ∫ 0 d (х) + ∫ 2 (х – 3) d (х) = 0 + 2 (–– – 3 х ) =
- ∞ 3 2 3
Х2 9
= 2 ( ––– – 3х – –– + 9 ) = х2 – 6 х + 9
2 2
3 4 х
При Х > 2 F (Х) = ∫ 0 d (х) + ∫ 2 (х – 3) d (х) + ∫ 0 d (х) =
- ∞ 3 4
 Х2 4 42 32
Х2 4 42 32
= 0 + 2 ( ––– – 3х) + 0 = 2 ( –––– – 12 – ––– + 9) = 16 – 24 –9 + 18 = 1
2 3 2 2
Отже, закон розподілу випадкової величини Х має вигляд:
 0, Х ≤ 3
0, Х ≤ 3
 F (Х) = х2 – 6 х + 9 3 < Х ≤ 4
F (Х) = х2 – 6 х + 9 3 < Х ≤ 4
 1, Х > 4
1, Х > 4
Будуємо графіки функцій f(х) та F(Х).
Графік функції f(Х):
f (Х)
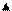


 2
2








 Х
Х
0 1 2 3 4
Графік функції F(Х):
 F (Х)
F (Х)
 |


 1
1






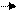
0 1 2 3 4 Х
Завдання 7.
Відомо математичне сподівання а і середнє квадратичне відхилення σ нормально розподіленої випадкової величини Х. Знайти імовірність попадання цієї величини в заданий інтервал (α,β)
а = 2, σ = 5, α = 4, β = 9.
Розв'язок
Імовірність попадання нормально розподіленої випадкової величини Х в заданий інтервал (α,β) розраховуємо за формулою:
β – а α – а
Р (α < Х < β) = Ф ( ––––– ) – Ф ( ––––– )
σ σ
де а – математичне сподівання;
σ – середнє квадратичне відхилення
(α,β) – заданий інтервал
1 х
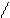
 Ф (х) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
Ф (х) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
 2 π 0
2 π 0
α – а β – а
х1 = –––––––; х2 = –––––––;
σ σ
Знаходимо х1 та х2
4 – 2 2
х1 = ––––––– = –––– = 0,4;
5 5
9 – 2 7
х2 = ––––––– = ––– = 1,4
5 5
За таблицею значень функції Лапласа знаходимо:
Ф ( 0,4 ) = 0,1555
Ф (1,4) = 0,4190
Звідси, Р (4 < Х < 9) = Ф (1,4) – Ф ( 0,4) = 0,4190 – 0,1555 = 0,2635
Завдання 8.
Дано закон розподілу дискретної двомірної випадкової величини (Х,Y). Знайти коефіцієнт кореляції між Х та Y.
| Y Х | –1 | ||
| 0,15 | 0,15 | 0,25 | |
| 0,15 | 0,10 | 0,20 |
Розв'язок
Коефіцієнт кореляції обчислюємо за формулою:
К
ρ = ––––––
σх σу
де К = М (ХY) – М(Х) · М(Y) - коваріація
М (ХY) – математичне сподівання двомірної випадкової величини ХY
М (Х) – математичне сподівання випадкової величини Х
М (Y) – математичне сподівання випадкової величини Y
σх – середнє квадратичне відхилення випадкової величини Х
σу– середнє квадратичне відхилення випадкової величини Y
Знаходимо необхідні показники.
М (ХY) = ΣΣхyрхрy = 1 (–1 ·0,15+0 ·0,15+1 ·0,25)+
+ 2 (–1 ·0,15+0 ·0,10+1 ·0,20) =1·0,1 + 2 · 0,05 = 0,2
М (Х) = Σхрх = 1 (0,15+0,15 + 0,25)+ 2 (0,15+0,10+0,20) =
= 1·0,55 + 2 ·0,45 = 0,55 + 0,9 = 1,45
М (Y) = Σyрy = –1 (0,15+0,15)+ 0 (0,15+0,10)+ 1 (0,25 + 0,20) =
= – 1·0,30 + 0 ·0,25 + 1 · 0,45= – 0,30 + 0,45 = 0,15
К = 0,2 – 1,45 ·0,15 = 0,2 – 0,2175 = – 0,0175
σх = М(Х2) – [М(Х)] 2 = 12 (0,15+0,15 + 0,25)+ 22 (0,15+0,10+0,20) –
– 1,452 = 1·0,55 + 4 ·0,45 – 2,1025 = 0,55 + 1,8 – 2,1025 = 0,2475
σу = М(Y2) – [М(Y)] 2 = –12 (0,15+0,15)+ 02 (0,15+0,10)+
+ 12 (0,25 + 0,20) – 0,152 = 0,30 + 0,45 – 0,0225 = 0,7275
Звідси коефіцієнт кореляції між Х та Y становить:
– 0,0175 – 0,0175
ρ = –––––––––––––– = –––––––––– = – 0,097
0,2475 · 0,7275 0,18
Отже, кореляційний зв’язок між Х та Y є оберненим, слабким.
Завдання 9.
За результатами спостережень над випадковою величиною Х знайти вибіркову функцію розподілу, вибіркове середнє і незсунену оцінку дисперсії.
| хі | – 3 | – 2 | – 1 | |||
| nі |
Розв'язок
Знаходимо вибіркову функцію розподілу за формулою:
μn
Fn (Х) = –––––
n
де μn – кількість значень випадкової величини Х, менших за хі
n = 50 – загальна кількість спостережень.
При Х ≤ –3 μn = 0; Fn (Х) = ––––– = 0
При –3 < Х ≤ –2 μn = n1 = 1; Fn (Х) = ––––– = 0,02
При –2 < Х ≤ –1 μn = n1 + n2 = 1 + 7 = 8; Fn (Х) = ––––– = 0,16
При –1 < Х ≤ 1 μn = n1 + n2 + n3 = 1 + 7 + 25 = 33; Fn (Х) = ––––– = 0,66
При 1 < Х ≤ 2 μn = n1+ n2 + n3+ n4 = 1 + 7 + 25 + 10 = 43; Fn (Х) = –––– = 0,86
При 2 < Х ≤ 3 μn = n1 + n2 + n3 + n4 + n5 = 1 + 7 + 25 + 10 + 5 = 48;
Fn (Х) = ––––– = 0,96
При Х > 3 μn = n = 50; Fn (Х) = ––––– = 1
Отже, вибіркова функція розподілу має вигляд:
 0, Х ≤ –3
0, Х ≤ –3
 0,02, –3 < Х ≤ –2
0,02, –3 < Х ≤ –2
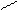 0,16 –2 < Х ≤ –1
0,16 –2 < Х ≤ –1

 Fn (Х) = 0,66 –1 < Х ≤ 1
Fn (Х) = 0,66 –1 < Х ≤ 1
0,86 1 < Х ≤ 2
 0,96 2 < Х ≤ 3
0,96 2 < Х ≤ 3
1, Х > 3
Знаходимо вибіркове середнє:
_ 1 1
хв = –– Σ хі nі = ––– [ (–3) ·1+(–2 ) ·7+(–1) ·25+1·10+2 ·5 + 3·2] =
n 50
– 3 – 14 – 25 + 10 + 10 + 6 –16
= –––––––––––––––––––––– = –––– = – 0,32
50 50
Знаходимо вибіркову дисперсію.
1 _ 1
δ2в = –– Σ х2і nі – ( хв )2 = ––– [ (–3) 2 ·1+(–2 ) 2 ·7+ (–1)2 ·25+12·10+
n 50
9 + 28 + 25 + 10 + 20 + 18
+ 22 ·5 + 32 ·2] – (–0,32)2 = –––––––––––––––––––––––– – 0,1024 =
= –––– – 0,1024 = 2,2 – 0,1024 = 2,0976
Знаходимо незсунену оцінку дисперсії.
n 50
S2 = ––––– · δ2в = ––– ·2,0976 = 2,1404
n – 1 49
Завдання 10.
У відділі технічного контролю було виміряно n = 200 втулок з партії, виготовленої одним автоматичним верстатом. У таблиці дано відхилення діаметрів від номіналу (у мікронах) після групування. Знайти вибіркове середнє і незсунену оцінку дисперсії для цих відхилень. Знайти надійні межі для математичного сподівання а відхилення діаметру від номіналу для генеральній сукупності при надійному рівні 0,95.
| Межі відхи-лення | [–20,–15) | [–15,–10) | [–10,–5) | [–5,0) | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) |
| nі |
Розв'язок
Всі необхідні обчислення будемо здійснювати за допомогою наступної таблиці:
| Межі відхи-лення | Середина інтервалу (варіанти хі) | Кількість втулок (частоти nі) | Розрахункові показники | ||
| хі nі | хі2 | хі2 nі | |||
| [–20,–15) | – 17,5 | -122,5 | 306,25 | 2143,75 | |
| [–15,–10) | – 12,5 | -125 | 156,25 | 1562,5 | |
| [–10,–5) | – 7,5 | -112,5 | 56,25 | 843,75 | |
| [–5,0) | – 2,5 | -62,5 | 6,25 | 156,25 | |
| [0,5) | 2,5 | 122,5 | 6,25 | 306,25 | |
| [5,10) | 7,5 | 307,5 | 56,25 | 2306,25 | |
| [10,15) | 12,5 | 156,25 | 4062,5 | ||
| [15,20) | 17,5 | 297,5 | 306,25 | 5206,25 | |
| [20,25) | 22,5 | 157,5 | 506,25 | 3543,75 | |
| [25,30) | 27,5 | 82,5 | 756,25 | 2268,75 | |
| Сума | х | х |
Знаходимо вибіркове середнє:
_ 1 1
хв = –– Σ хі nі = –––– ·870 = 4,35
n 200
Знаходимо вибіркову дисперсію.
1 _ 1
δ2в = –– Σ х2і nі – ( хв )2 = ––– ·22400–(4,35) 2 = 112 – 18,9225 = 93,0775
n 200
Знаходимо незсунену оцінку дисперсії.
n 200
S2 = ––––– · δ2в = –––– ·93,0775 = 93,545
n – 1 199
Знаходимо надійні межі для математичного сподівання а відхилення діаметру від номіналу для генеральній сукупності.

 _ S2
_ S2
а = хв ± t · ––––
n
де t – коефіцієнт довіри, який визначається із співвідношення:
2Ф(t) = γ
γ = 0,95 – рівень довіри
1 t
 Ф (t) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
Ф (t) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
 2 π 0
2 π 0
γ 0,95
Ф(t) = ––– = –––– = 0,475
2 2
За таблицею значень функції Лапласа визначаємо, що значенню функції Ф(t) = 0,475 відповідає значення t = 1,96. Звідси маємо:
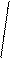

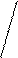

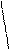
 93,545
93,545
а = 4,35 ± 1,96 · –––––– =4,35± 1,96 · 0,4677 = 4,35 ± 1,96 ·0,684 =
= 4,35 ± 1,34
4,35 – 1,34 ≤ а ≤ 4,35 + 1,34
3,01 ≤ а ≤ 5,69
Отже, математичне сподівання а відхилення діаметру від номіналу для генеральній сукупності втулок з рівнем надійності 0,95 знаходиться у межах від 3,01 до 5,69 мікрон.
Завдання 11.
Знайти надійний інтервал для оцінки математичного сподівання а
_
нормального розподілу з надійністю 0,95, знаючи вибіркову середню х, об’єм
вибірки n і середнє квадратичне відхилення σ.
_
х = 75,09; n = 196; σ=14.
Розв'язок
Знаходимо надійний інтервал для оцінки математичного сподівання а нормального розподілу.

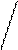
 _ σ2
_ σ2
а = х ± t · ––––
n
де t – коефіцієнт довіри, який визначається із співвідношення:
2Ф(t) = γ
γ = 0,95 – рівень довіри
1 t
 Ф (t) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
Ф (t) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
 2 π 0
2 π 0
γ 0,95
Ф(t) = ––– = –––– = 0,475
2 2
За таблицею значень функції Лапласа визначаємо, що значенню функції Ф(t) = 0,475 відповідає значення t = 1,96. Звідси маємо:

142
а = 75,09 ± 1,96 · –––––– =75,09± 1,96 · 1 = 75,09 ± 1,96
75,09 – 1,96 ≤ а ≤ 75,09 + 1,96
73,13 ≤ а ≤ 77,05
Отже, математичне сподівання а нормального розподілу для генеральній сукупності з рівнем надійності 0,95 знаходиться у межах від 73,13 до 77,05.
| <== попередня сторінка | | | наступна сторінка ==> |
| | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |