Методика вивчення геометричного матеріалу дітьми дошкільного віку

Цілісність сприймання предметів, властива дітям дошкільного віку, не дозволяє самостійно диференціювати окремі ознаки предметів і лише під керівництвом вихователя діти навчаються визначати форму предметів та структуру предмета (його частини). Геометрична форма з об’єкта вивчення поступово стає сенсорним еталоном для визначення форми предметів оточуючого середовища. Тому важливо у 3-4 роки надавати увагу сенсорному вихованню, а у 5-6 років формуванню системності знань про геометричні фігури та розвивати прийоми геометричного мислення.

Вчені А.М. Пишкало, А. А. Столяр визначають етапи формування «геометричних знань»: І рівень – фігура сприймається цілісно, без виділення складових; не диференціюються «схожі» фігури і кожна із них сприймається окремо; ІІ рівень – дитина визначає елементи фігури, встановлює відношення між ними та між різними фігурами, але ще не робить узагальнень; 3) дитина встановлює зв’язки між властивостями та структурою фігур, зв’язки між самими властивостями геометричних фігур. На цьому рівні дітьми встановлюється залежність між назвою фігури та її структурою. На ІІІ рівні діти здійснюють перетворення геометричних фігур (перекомбінування), їх моделювання, побудову за зразком на лінованому папері, геометричне конструювання (побудова фігур із паличок, паперове конструювання).

Подамо особливості вивчення геометричного матеріалу у різних вікових групах.

Середня група. 1. Закріплюється уміння розрізняти круг і квадрат, названі фігури і трикутник. Варіативною ознакою виступає колір і величина, а інваріантною – форма. Побудова серіаційних рядів за величиною (зростання, спадання ознаки), за кольором (за інтенсивністю кольору).

2. Вибір серед геометричних фігур тих, що мають однакову форму. Використовуються геометричні фігури однакової форми для лічби та порівняння їх кількості.

3. Групування та порівняння фігур за двома ознаками: кольором і величиною, кольором і формою, величиною і формою.

4. Етапи з вивчення нової геометричної фігури: сенсорне обстеження та побудова його перцептивного образу, визначення інваріантної форми в оточуючих предметах, подання форми як сенсорний еталон, використання геометричних фігур як сенсорний еталон, ознайомлення із властивостями геометричних фігур, побудова геометричних фігур на лінованому папері за зразком. оточую

Старша група. 1. Пропонуються завдання на порівняння властивостей, ознак предметів та виконання узагальнення: у чотирикутника 4 сторони, 4 кути, 4 вершини; у кола немає кутів.

2. Завдання на розрізнення понять межі фігури та її внутрішньої області. Наприклад, завдання обвести фігуру по контуру олівцем певного кольору, а внутрішню частину – іншого. Висновок: Геометрична фігура – це контур та внутрішня частина.

3. Завдання на порівняння предметів з еталонами – геометричними фігурами.

4. Дидактичні ігри «Геометричне доміно», «Геометричне лото».

5. Геометричне конструювання нових геометричних фігур складанням, наприклад, із двох трикутників квадрат, з двох трикутників – прямокутник тощо. Поділ геометричної фігури на частини.

Підготовча група. Основне завдання – розширити та систематизувати знання про геометричні фігури. Діти ознайомлюються із п’ятикутником, шестикутником, багатокутником, креслять геометричні фігури (квадрат, прямокутник) на лінованому папері. Дітям пропонуються завдання на 1) перетворення геометричних фігур; 2) встановлення родово-видових відношень між геометричними фігурами; 3) використання геометричних фігур як лічильного матеріалу.

Подамо приклади паперового конструювання, а саме, виготовлення з паперу зразків ігор „Піфагор” та „Чарівне коло”.

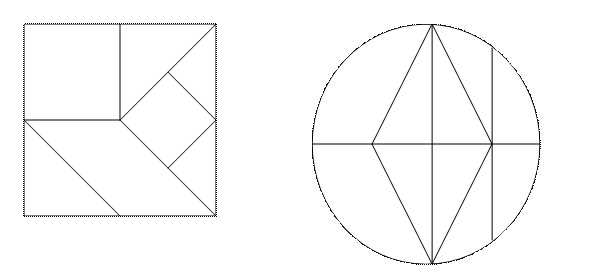
Методика навчання дітей дошкільного віку розв'язувати текстові задачі

Якщо розглядати розвиток особистості дитини як процес якісних змін у мисленні, формуванні його психічних функцій та пізнавальних процесів, то це і є запорукою вироблення операційного досвіду, необхідного для подальшого активного впливу на зовнішнє середовище. Інструментом досягнення цілей педагогічного впливу на дитину виступають задачі. Традиційним є підбір задач, який можна охарактеризувати як однофункціональні. При їх виконанні реалізується одна дидактична мета, один оперативний спосіб “бачення” суті вправи і застосовується при їх виконанні одна чи дві розумові операції. Це уодноманітнює сприймання навколишньої дійсності, спричиняє формування інертності мислення, не розвиває розум, притупляє емоційну сферу дитини. Завдання, складені за принципом багатофункціональності, передбачають виконання кількох операцій мислення на конкретному змістовному матеріалі чи побутово-сюжетній ситуації, ставлять дитину в умови вияву самостійної ініціативи, напруги розумових сил і реалізації природного потягу до пізнання нового

Роль математичних задач у навчанні дітей дошкільного віку математиці полягає у: 1) підготовці до формування умінь розв’язування задач у початкових класах; 2) розвитку мислитель них операцій та інтелектуальних операцій (аналізу, синтезу, порівняння, моделювання, узагальнення); 3) вихованні якостей особистості (наполегливості, акуратності, волі, терпіння, досягнення мети діяльності, пробудження інтересу до математики).

Формування уміння розв’язувати текстові задачі складає одну із провідних ліній розвитку математичного мислення молодших школярів, оскільки передбачає виконання учнями розумових операцій на різних етапах роботи над задачею: аналізі числових даних (виокремлення семантичного змісту, співставлення характеристик об’єктів дії з реальною ситуацією, конкретизацію числових параметрів та їх порівняння), розборі задачі аналітичним, синтетичним чи аналітико-синтетичний способом, складанні плану розв’язування у вигляді послідовності взаємопов’язаних дій, розв’язанні, перевірці правильності відшукання розв’язку різними способами та формулюванні відповіді. Розбір задачі виступає центральною ланкою розв’язування задачі та розвитку процесів мислення, які і гарантують усвідомленість розмірковувань учнів. У завдання вчителя входить не тільки навчання учнів визначати відомі і шукані величини, за настановою відшукувати зв’язок між ними, але і вибудовувати ланцюжок логічно поєднаних між собою умовисновків щодо вибору та обґрунтування арифметичних дій, послідовності їх виконання. Якраз розбір задачі задає мотиваційний прорив у формуванні умінь розв’язувати будь-яку арифметичну задачу. Уважаємо, що підсилення етапу розбору простих і складених задач методичними підходами, спрямованими на оволодіння умінням обґрунтовувати вибір арифметичної дій, складає реальний напрям усвідомленого розв’язування задач.

Ефективність розбору задачі залежить від кількох методичних позицій, а саме: а) диференціації понять „задача“ та „задачна ситуація“; б) оптимального, домірного використання засобів наочності, функції яких для розв’язування задач можна визначити як бінарні (спрямованістю на ілюстрування зв’язків між шуканими та даними величинами; створення дидактичних ситуацій „інтелектуальної напруги“, коли результат дії не можна відшукати за допомогою способів прилічування чи перелічування); в) вибір арифметичної дії має забезпечуватися використанням засобів наочності та коротким записом, які ставлять учня перед необхідністю знаходження відповіді задачі за допомогою арифметичної дії; г) обґрунтування учнями вибору арифметичної дії полягає в аргументуванні використання опорних слів, аналізу сюжетного матеріалу та моделі задачі.

Диференціація понять „задача“ і „задачна ситуація“ полягає, на нашу думку, у тому, наскільки ці поняття відповідають означенню задачі, яке подається у математиці як науці та методиці викладання математики у загальноосвітній школі. Під арифметичною задачею розуміється вимога знайти значення невідомої величини за даними числами та умовами, що пов’язують відомі та шукані величини. [1; 2]. В означенні не вказується яким чином знаходиться відповідь – за допомогою арифметичної дії чи на основі роботи з наочністю. Але це є суттєвий момент для формування у молодших школярів уміння розв’язувати арифметичну задачу, оскільки „задачна ситуація“ характерна для розв’язування задач за допомогою наочності, а „задача“ – арифметичної дії. Робота із „задачною ситуацією“ та „задачею“ розділені у часі, оскільки розв’язування задачі на основі арифметичних дій може бути впроваджена тільки після вивчення таблиць додавання (віднімання) та множення (ділення). Тому „задачна ситуація“ є обов’язковим дидактичним завданням на підготовчому етапі у формуванні уміння розв’язувати арифметичні задачі.

Оскільки формування уміння розв’язувати будь-яку складену задачу базується на умінні розв’язувати прості, зупинимося на питаннях методики роботи над простими задачами різних типів з урахуванням раніше визначених методичних позицій.

Подамо схему роботи із формування уміння розв’язувати прості задачі та визначимо систему завдань на кожному із етапів роботи над задачами, а саме: підготовчому, ознайомлення із задачею певного типу та закріплення.

Проілюструємо систему роботи на прикладі задачі на знаходження суми. На підготовчому етапі основними дидактичними цілями виступають: актуалізація опорних знань щодо змісту арифметичної дії додавання; повторення поняття „задача“ та структури задачі; розгляд „задачних ситуацій“, які базуються на використання „відкритої“ наочності та безпосередньо демонструють зв’язки між об’єктами дій задачі; складання прикладів за малюнком, за предметною наочністю, за вербальною настановою, з використанням елементів моделювання на основі образів уяви та предметів-замінників; повторення табличних випадків додавання;

Завдання № 1. Скласти приклад за малюнком.

Завдання № 2. Скласти приклад за наочністю (предметною).

Завдання № 3. Скласти приклад за наочністю (зображувальною).

Завдання № 4. Скласти приклад за наочністю з використанням демонстраційних предметів-замінників.

Завдання № 5. Скласти приклад за наочністю з використанням предметів-замінників (з оформленням у зошитах).

Завдання № 6. Чи буде задачею?

Завдання № 7. Назвати умову і запитання задачі.

Завдання № 8. Скласти задачу за малюнком.

Завдання № 9. Скласти задачу за прикладом.

Завдання № 10. Повторити табличні випадки додавання (віднімання).

Переглядів: 6234

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.