Хвильова функція та її фізичний зміст. Рівняння Шредінгера

З відкриттям хвильових властивостей частинок стало зрозуміло, що для опису руху мікрочастинки закони Ньютона не підходять. Тобто необхідною була така механіка, що враховувала б хвильові властивості частинок. І нею стала квантова механіка. Така механіка була створена завдяки працям де Бройля, Гейзенберга, Шредінгера, Дірака та інших. Квантова механіка – це теорія руху частинок малої маси, мікрочастинок, яка дає змогу врахувати їхні хвильові і корпускулярні властивості.

Стан частинки у квантовій механіці визначається хвильовою функцією, що є функцією координат і часу (ψ-функція). Квадрат модуля псі-функції для точки, помножений на елемент об’єму, що включає цю частинку, визначає ймовірність знаходження частинки в цьому об’ємі:

, де dP − ймовірність, dV − елемент об’єму.

Квадрат модуля ψ-функції є густина ймовірності (тобто визначає густину величини в такому ж розумінні, як густина енергії, густина заряду тощо).

Фізичний зміст має не сама псі-функція, а квадрат її модуля, який визначає ймовірність перебування частинки в даній точці простору. Інакше кажучи, величина визначає інтенсивність хвиль де Бройля. Хвильова функція має задовольняти умову, яка називається умовою нормування ймовірностей:

Це інтеграл по безмежному нескінченному простору. Умова нормування ймовірностей означає, що перебування частинки десь у просторі є достовірна подія, і її ймовірність дорівнює 1.

У квантовій механіці постає важлива проблема про відшукання такого рівняння, яке б мало таке саме значення, як рівняння руху Ньютона для класичної механіки. Нагадаємо, що рівняння Ньютона дають змогу за відомими силами, які діють на тіло, і певними початковими умовами визначити для будь-якого моменту часу координати тіла та його швидкість, тобто описати рух тіла в просторі і часі. Розв'язуючи аналогічну задачу в квантовій механіці, необхідно врахувати те, що частинки мають хвильові властивості. Положення частинки описується заданням псі-функції, тому рівняння має бути хвильовим.

У 1926 році Шредінгер отримав основне рівняння квантової механіки:

де

де і – уявна одиниця, m – маса частинки, U – її потенціальна енергія.

Це часове рівняння. Але дуже часто важливо знайти стаціонарні розв'язки рівняння Шредінгера, які не містять часу. Вони мають значення для тих задач, у яких потенціальна енергія не залежить від часу, а залежить тільки від координат, тобто U = U(x, y, z).

Таке рівняння називається стаціонарним рівнянням Шредінгера:

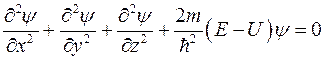Значення енергії Е – повної енергії частинки, при яких має розв'язок це диференціальне рівняння, називаються власними значеннями енергії. Власному значенню енергії E відповідає власна функція .

Якщо потенціальна енергія залежить тільки від координати х, то рівняння Шредінгера називається одновимірним і набирає вигляду:

де m − маса частинки,

E − повна енергія частинки,

U(x) − потенціальна енергія частинки,

(E-U(x)) − кінетична енергія частинки,

Ψ − псі-функція.

Зауваження. У квантовій механіці не порушується принцип причинності. Якщо задано псі-функцію для моменту часу , то можна визначити її значення для моменту часу 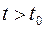. Тобто стан мікрооб'єкта, визначений у деякий момент часу , однозначно визначає його подальший стан.

Рівняння Шредінгера дає змогу розв'язувати важливі практичні задачі і розраховувати стаціонарні стани руху частинок у різних зовнішніх полях. Розглянемо деякі з них.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.032 сек.