Вузли та їх типи

1. Означення вузла. Майже всі знайомі з найпростішими вузлами, такими як простий вузол(рис.1) та вісімка( рис.2).

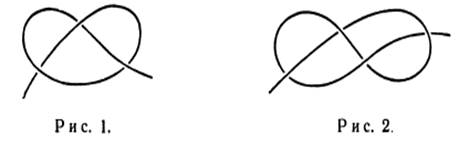
Не важко побачити, що ці вузли є різними, так як їх не можна перевести один в інший не просовуючи один кінець через петлю. Але досліди з шматком мотузки не дають нам доказів того, що це взагалі не можливо. Тобто, наша задача полягає в тому, щоб довести математичними методами, що ці об’єкти дійсно різні.

Математики можуть доводити будь-що тільки відносно математичних об’єктів, тому слід одразу визначитись з математичним означенням вузла та того, коли два вузли мають розглядатися рівними.

Очевидно, що вісімка може перейти в простий вузол зв’язуванням і розв’язуванням, але якщо ці операції допустити, то всі вузли стають еквівалентними між собою. Слід одразу заборонити ці операції, а також позбавитись від кінців( кінці можна склеїти між собою або прибрати на безкінечність). Відповідно до цього під вузлом ми будемо розуміти підмножину трьохвимірного простору, гомеоморфну колу. Точніше означення матиме такий вигляд: К є вузлом, якщо існує гомеоморфізм одиничного кола С в трьохвимірний простір R³, образ якого співпадає з К. Під колом С маємо на увазі множину точок (х, у) площини R², які задовольняють рівняння х²+у²=1.

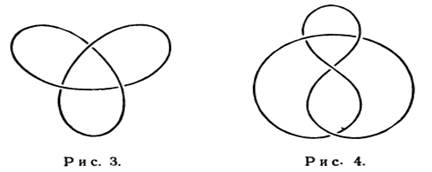
Рисунки 3 і 4 показують, як тепер виглядають простий вузол та вісімка. У такій формі простий вузол найчастіше називають трилисником. Вісімка частіше носить назву вузол Лістінга або чотирикратний вузол.

Розглянемо питання, коли два вузла К₁та К₂можуть бути рівними. Звернемо увагу на те, що обидва вузла є гомеоморфними одиничному колу, тобто гомеоморфні між собою. Завузленість не є внутрішньою топологічною властивістю простору, який складається з усіх точок вузла, але характеризує спосіб, за допомогою якого цей простір вкладається в R³. Теорія вузлів є частиною тривимірної, а не одновимірної топології. Якщо змінити положення мотузки з одного в інше шляхом закручування, то ця деформація визначає взаємно однозначну відповідність між точками цих двох положень. Так як переріз мотузки заборонений, то ця відповідність неперервна в дві сторони. Крім того, природно вважати, що рух мотузки супроводжується рухом оточуючих молекул повітря, який визначає неперервне в обидві сторони перемішування точок всього простору. Ці роздуми ведуть до наступного означення: вузли К₁та К₂еквівалентні, якщо існує гомеоморфізм простору R³ на себе, який відображає К₁на К₂.

Еквівалентні вузли називаються вузлами одного типу, а клас еквівалентних вузлів – типом вузла. Вузли, еквівалентні незавузленому колу х²+у²=1, z=0, називаються тривіальними і утворюють тривіальний тип. Аналогічно тип простого вузла або вісімки визначається як клас еквівалентності, представлений відповідним вузлом. Ці вузли належать до різний типів, тому вони не є еквівалентними між собою.

3.Ручні та дикі вузли. Полігональний вузол – це такий вузол, який є об’єднанням скінченої кількості замкнених прямолінійних відрізків, які називаються сторонами. Кінці цих відрізків називаються вершинами вузла. Вузол називається ручним, якщо він еквівалентний полігональному вузлу. В іншому випадку він називається диким. Відмінність між ручними і дикими вузлами має первинну важливість, тому що більша частина теорії вузлів застосовується тільки до ручних вузлів.

Доречно поцікавитись, який клас вузлів, відмінний від полігональних, складається з ручних вузлів. Частковою відповіддю на це питання буде наступна теорема.

(2.1) Якщо вузол, параметризований довжиною дуги,

належить класу С¹, то він є ручним.

Доведення цієї теореми є досить громістким, але є прямим і використовує техніку диференціального числення. Припущення відносно вузла К полягають в тому, що він напрямлений і заданий як образ векторнозначної функції р(s)= (x(s), y(s), z(s)) довжини дуги s, яка має неперервні перші похідні. З цього випливає, що будь-який достатньо гладкий вузол є ручним.

3.Проекції вузлів.Зазвичай вузли задаються своєю проекцією. Наприклад, на рис. 3 і рис. 4 зображено проекції «клеверного листа» та вісімки відповідно. Розглянемо проекцію

P : R³ -–> R³,

визначену відношеннямР(х, у, z) = (x, у, 0). Точка р, що належить образу проекції РК, називається кратною, якщо її прообраз Р^-1 р містить більш ніж одну точку вузла К. Порядком точки р є РК називається потужність множини (Р^-1 р) ∩ К. Тому подвійна точка – це точка кратності два, потрійна точка – точка кратності три і т. д. Можуть зустрічатися точки безкінечного порядку. Взагалі, образ вузла РК може бути досить складним відносно кратних точок та їх типів. Такий вузол можна замінити еквівалентним йому, образ якого буде досить простим при проекції. Критерій достатньої «простоти» образу для полігонального вузла полягає в тому, щоб вузол був у регулярному положенні. Означення має вигляд: полігональний вузол К знаходиться у регулярному положенні, якщо: І) всі його кратні точки є подвійними і їх кількість скінчена, ІІ) жодна подвійна точка не є образом вершини вузла К. Друга умова гарантує, що кожна подвійна точка є перетином, як показано на рис. 6а. Перетини типу, вказаного на рис. 6b, заборонені.

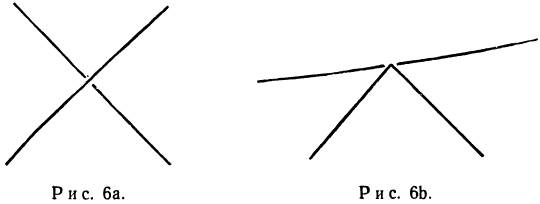
Будь-яка подвійна точка проекції полігонального вузла в регулярному положенні є образом рівно двох точок вузла. Точка, у якої координата z більша, називається перехідною, а друга відповідно прохідною.

(3.1) Будь-який полігональний вузол переходить як завгодно малим поворотом простору R³ в еквівалентний йому полігональний вузол в регулярному положенні.

Доведення. Геометрична ідея доведення полягає у тому, що фіксується вузол К, а змінюється проекція. Кожен пучок паралельних прямих в R³ визначає проекцію простору R³ на площину, яка проходить через початок координат перпендикулярно пучку, який розглядається. Розширимо попереднє означення регулярного положення так, щоб мало сенс питання, чи розміщений вузол К у регулярному положенні відносно деякої проекції. При цьому зручно розглянути простір R³ як підмножину дійсного проективного трьохвимірного простору Р³ .

Тоді всякій проекції можна співставити точку перетину будь-якою прямою, паралельною напряму проекції, з нескінченно віддаленою проективною площиною Р². Ця відповідність взаємно однозначна. Нехай Q – множина точок площини Р², які відповідають проекціям, відносно яких вузол К не лежить у регулярному положенні. Покажемо, що множина Q ніде не щільна в Р². Звідси буде слідувати, що існує проекція Р₀, відносно якої вузол К займає регулярне положення і яка як завгодно близька до проекції Р вздовж осі z. Після цього для остаточного доведення досить розглянути довільний поворот простору R³, який переводить пряму Р₀^-1(0, 0, 0) у вісь z.

Для доведення того, що множина Q ніде нещільне в Р², розглянемо спочатку множину всіх прямих, які об’єднують вершини вузла К з його сторонами. Вона перетинає площину Р² по скінченній кількості прямолінійних відрізків, об’єднання яких позначимо через Q₁. Будь-яка проекція, яка відповідає точці з множини Р² - Q₁, повинна задовольняти умову ІІ) означення регулярного положення. Більше того, вона може мати скінченне число кратних точок, з яких не одна не має безкінечного порядку. Залишилось показати, що можна позбавитись від кратних точок порядку n≥3. Це зробимо наступним чином. Розглянемо три прямі, які взаємно перетинаються і кожна з яких містить деяку сторону вузла К. Сукупність прямих, яка перетинає всі ці прямі, утворює поверхню другого порядку, яка перетинає Р² по деякому конічному перерізу.

Нехай Q₂– перетин всіх таких перерізів(їх скінченна кількість). Образ вузла К відносно будь-якої проекції, яка відповідає деякій точці множини

Р² - (Q₁ ∪ Q₂), не має кратних точок порядку n≥3. Ми показали, що

Р² – (Q₁ ∪ Q₂) ⊂ Р²– Q.

Q є підмножиною множини Q₁ ∪ Q₂, яка ніде нещільна в Р². Цим завершується доведення (3.1).

Отже, будь-який ручний вузол еквівалентний полігональному вузлу в регулярному положенні.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.