
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Дискретні та неперервні випадкові величини. Закони розподілу їх імовірностей
Розглянемо такий простір елементарних подій, в якому кожній елементарній події 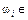 Ώ відповідає одне і лише одне число х або набір чисел
Ώ відповідає одне і лише одне число х або набір чисел 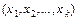 , тобто на множині Ώ визначена певна функція
, тобто на множині Ώ визначена певна функція 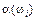 , яка кожній елементарній події
, яка кожній елементарній події 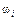 ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
Цю функцію називають випадковою величиною. У разі, коли 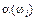 відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
Схематично одновимірну випадкову величину унаочнює рис. 19.
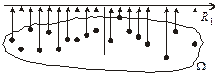
Рис. 19
Отже, величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.
Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.
Приклад 1. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Навмання беруть одне число. Елементарними подіями будуть такі: поява одного з чисел 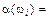 1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень
1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень 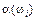 є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
Приклад 2. Вимірюється сила струму за допомогою амперметра. Результати вимірювання, як правило, округлюють до найближчої поділки на шкалі для вимірювання сили струму. Похибка вимірювання, що виникає внаслідок округлення, являє собою неперервну випадкову величину.
Випадкові величини позначають великими літерами латинського алфавіту X, Y, Z, ... , а їх можливі значення — малими х; у; z, ... .
Для опису випадкової величини необхідно навести не лише множину можливих її значень, а й указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.
З цією метою вводять поняття закону розподілу ймовірностей.
Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.
Закон розподілу дискретної випадкової величини Х можна задати в табличній формі або за допомогою ймовірнісного многокутника.
У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:
| Х = хі | х1 | х2 | х3 | ...... | хk |
| Р(Х = хі) = рі | р1 | р2 | р3 | ..... | рk |
Оскільки випадкові події (Х = хj) і (Х = хm) є між собою несумісними ((Х = хі) ∩ (Х = хm) = Æ, і 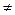 m; і, m = 1, 2, …, k) і утворюють повну групу
m; і, m = 1, 2, …, k) і утворюють повну групу 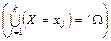 , то необхідною є така умова:
, то необхідною є така умова:
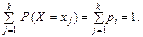 (61)
(61)
Рівність (61) називають умовою нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.
Закон розподілу ймовірностей можна унаочнити графічно.
Для цього візьмемо систему координат рі О хі, відклавши на осі абсцис можливі значення випадкової величини хі, а на осі ординат — імовірності рі цих можливих значень. Точки з координатами (хі; рі) послідовно сполучимо відрізками прямої. Утворену при цьому фігуру називають імовірнісним многокутником.
Приклад 3. За заданим у табличній формі законом розподілу дискретної випадкової величини Х:
| Х = хі | –2,5 | 3,5 | 6,5 | |||
| Р(Х = хі) = рі | 0,1 | 0,2 | 0,1 | 0,3 | 0,2 | 0,1 |
побудувати ймовірнісний многокутник.
Розв’язання. Імовірнісний многокутник зображено на рис. 20
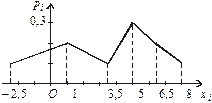
Рис. 20
Сума ординат імовірнісного многокутника завжди дорівнює одиниці.
2. Функція розподілу ймовірностей (інтегральна функція) та її властивості
Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(х), так звану інтегральну функцію.
Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей:
F(x) = P(X < x) (62)
Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х .
Наприклад, F(5) = P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис. 21.
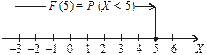
Рис. 21
Розглянемо властивості F(x):
1. 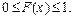
Ця властивість випливає з означення функції розподілу.
2. 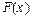 є неспадною функцією, а саме
є неспадною функцією, а саме 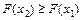 , якщо
, якщо 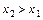 .
.
| ! |
Доведення.Позначимо відповідно А, В, С події (Х < x2), (Х < x1) і 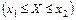 . Випадкові події В і С є несумісними (А
. Випадкові події В і С є несумісними (А 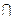 С = Æ) (рис. 22).
С = Æ) (рис. 22).
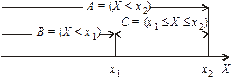
Рис. 22
Тоді подію А можна записати так:
А = В  С (А = В + С).
С (А = В + С).
За формулою додавання для несумісних випадкових подій (6) маємо:
Р(А) = Р(В  С) = Р(В) + Р(С)
С) = Р(В) + Р(С)
або
Р(Х < x2) = Р(Х < x1) + P(x1 £ Х £ х2). (63)
Звідси на підставі означення інтегральної функції F(x), дістаємо
F(x2) = F(x1) + P(x1 £ Х £ х2)
або
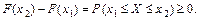 (64)
(64)
Отже,
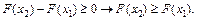
Із другої властивості F(x) випливають наведені далі висновки:
1. Імовірність того, що випадкова величина Х набуде можливого значення 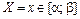 , дорівнює приросту інтегральної функції F(x) на цьому проміжку:
, дорівнює приросту інтегральної функції F(x) на цьому проміжку:
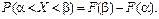 (65)
(65)
2. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює нулю:
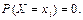
І справді, поклавши в (65) 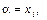
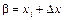 , дістанемо
, дістанемо
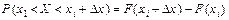 .
.
Коли 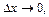 маємо:
маємо:
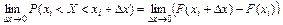 . (66)
. (66)
Оскільки при 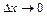 Х = хі, то
Х = хі, то
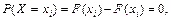
що й потрібно було довести.
Отже, для неперервної випадкової величини Х справджуються такі рівності:
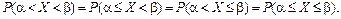 (67)
(67)
3. Якщо 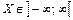 , виконуються два подані далі співвідношення.
, виконуються два подані далі співвідношення.
1) 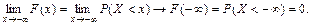
Оскільки подія Х < – ¥ полягає в тому, що випадкова величина набуває значення, яке міститься ліворуч від – ¥. А така подія є неможливою (Æ).
2) 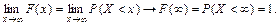
Подія Х < 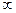 полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від + ¥. Ця подія є вірогідною (Ώ), оскільки будь-яке число X = x <
полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від + ¥. Ця подія є вірогідною (Ώ), оскільки будь-яке число X = x < 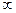 .
.
Із цих двох співвідношень випливає висновок: якщо можливі значення випадкової величини Х належать обмеженому проміжку [а; b], то
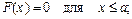
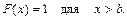 (68)
(68)
3. Щільність імовірностей (диференціальна функція) f (x) і її властивості
Для неперервних випадкових величин закон розподілу ймовір-ностей зручно описувати з допомогою щільності ймовірностей, яку позначають f (x).
Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):
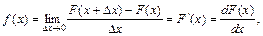 (69)
(69)
звідки 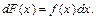
Оскільки
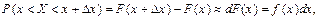
то добуток f (x) dx — ймовірність того, що випадкова величина Х міститиметься у проміжку [х, х + dx], де 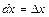 .
.
Геометрично на графіку щільності ймовірності f (x) dx відповідає площа прямокутника з основою dx і висотою f (x) (рис. 27а).

Рис. 27а
Властивості f (x)
1. 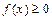 . Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.
. Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.
2. Умова нормування неперервної випадкової величини Х:
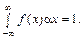 (70)
(70)
| ! |
Переглядів: 2895