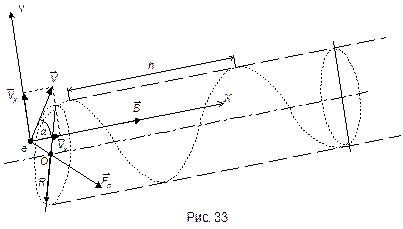- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Решение
Передаваемая мощность к потребителю равна 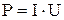 (1), где
(1), где 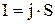 , (2) сила тока в линии передач,
, (2) сила тока в линии передач, 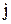 - плотность тока в проводе сечения
- плотность тока в проводе сечения 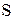 .
.
При прохождения тока по проводнику он нагревается. Это определит потери мощности, которые можно найти из закона Джоуля-Ленца.
Потеря мощности равна 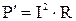 (3), где R - сопротивление двухпроводной линии
(3), где R - сопротивление двухпроводной линии 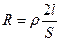 (4).
(4).
В формуле (4): l – расстояние до потребителя электроэнергии.
Потеря мощности определяется по формуле 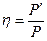 или, используя формулы (1) и (3), получим
или, используя формулы (1) и (3), получим 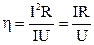 .
.
Отсюда напряжение 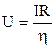 .
.
Используя формулы (2) и (4) получим 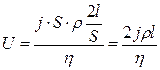 .
.
Проверим справедливость формулы по размерности величин:
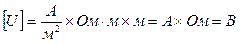 .
.
Вычислим значение искомого напряжения:
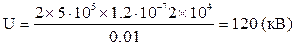 .
.
Ответ:  .
.
Пример №7. Два параллельных бесконечно длинных провода А и С, по которым текут в одном направлении токи силой I1 = I2 = I = 50 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию  поля, создаваемого проводниками с током в точке D, отстоящей от оси одного провода на расстоянии r1 = 5 см, от другого – на r2= 12 см.
поля, создаваемого проводниками с током в точке D, отстоящей от оси одного провода на расстоянии r1 = 5 см, от другого – на r2= 12 см.
| Дано: | Решение: |
| I1 = I2 = I = = 50 А d = 10 см = = 0,10 м r1 = 5 см = = 0,05 м r2 = 12 см = = 0,12 м | Воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций  и и  полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: 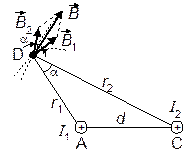 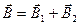 .
Модуль вектора В может быть найден по теореме косинусов: .
Модуль вектора В может быть найден по теореме косинусов: 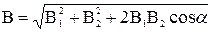 , где α – угол между векторами , где α – угол между векторами  и и  . .
|
 -? -?
|
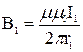 ;
; 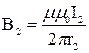 .
.
Тогда 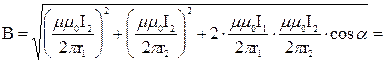
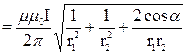 . (1)
. (1)
Угол α =ÐADC – как углы при вершинах треугольников с взаимно перпендикулярными сторонами.
Из DАDС по теореме косинусов запишем:
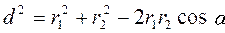 , откуда
, откуда 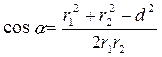 .
.
Подставим числовые значения и произведем вычисления:
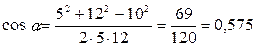 .
.
Подставив в формулу (1) числовые значения физических величин, получим:
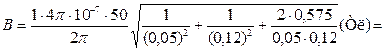
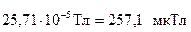
Ответ: В = 357,1 мкТл.
Пример №8. По тонкому стержню длиной l = 50 см равномерно распределен заряд q = 60 нКл. Стержень вращается с частотой ν = 12 с–1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии а = 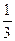 l от одного из его концов. Определить магнитный момент Pm, обусловленный вращением стержня.
l от одного из его концов. Определить магнитный момент Pm, обусловленный вращением стержня.
| Дано: | Решение: |
l =50 см = 0,50 м
q = 60 нКл = 60×10-9 Кл
ν= 12 с–1
а = 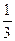 l l
| По определению магнитный момент плоского контура с током I равен:
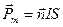 ,
где ,
где 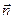 – единичный вектор нормали к плоскости контура S.
Выделим элемент стержня длиной dr с зарядом на нем – единичный вектор нормали к плоскости контура S.
Выделим элемент стержня длиной dr с зарядом на нем 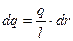 . При вращении стержня относительно оси О элементарный круговой ток в данном случае определяется выражением . При вращении стержня относительно оси О элементарный круговой ток в данном случае определяется выражением
|
| Pm -? |
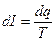 =νdq,
=νdq,
где n - частота вращения стержня. Магнитный момент элементарного кругового тока dPm = S×dI, где S – площадь, ограниченная окружностью, описываемой элементом стержня dr с зарядом dq (S = pr2, где r – радиус этой окружности).
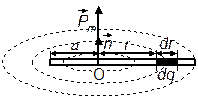 Тогда
Тогда 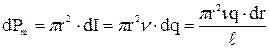 .
.
Магнитный момент Pm, обусловленный вращением стержня длиной l вокруг оси О, определяем интегрированием двух частей стержня: 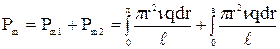 ,
,
где 0, 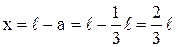 и
и 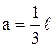 – пределы интегрирования.
– пределы интегрирования.
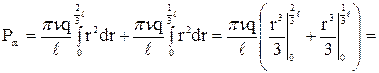
 .
.
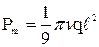 .
.
Произведем вычисления:
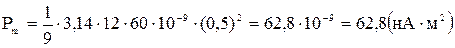 .
.
Ответ: Pm = 62,8 нА×м2.
Пример №9. Электрон движется в однородном магнитном поле (В=10 мТл) по винтовой линии, радиус которой R = 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость 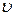 .
.
| Дано: | Решение: |
| В = 10 мТл = 10×10-3 Тл R = 1 см = 10-2 м h = 6 см = 6×10-2 м | Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом ( 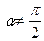 ) к линиям магнитной индукции. Разложим, как показано на рисунке, скорость ) к линиям магнитной индукции. Разложим, как показано на рисунке, скорость 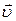 электрона на две составляющие: электрона на две составляющие:
|
Т-? 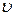 -? -?
|
 .
.
По модулю 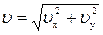 , где
, где 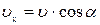 ;
; 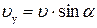 .
.
На электрон действует сила Лоренца 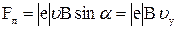
|
Сила Лоренца сообщает электрону нормальное ускорение 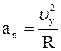 . Согласно второму закону Ньютона можно написать
. Согласно второму закону Ньютона можно написать 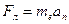 , или
, или 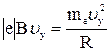 , откуда
, откуда 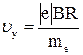 . Период обращения электрона связан с составляющей скорости
. Период обращения электрона связан с составляющей скорости 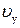 соотношением:
соотношением:  . Тогда получим:
. Тогда получим: 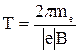 .
.
Произведем вычисления:
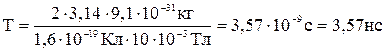 .
.
За время, равное периоду обращения Т, электрон пройдет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е. 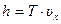 , откуда
, откуда
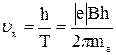 .
.
Модуль скорости электрона
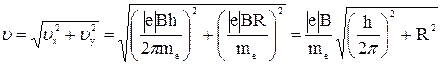 .
.
|
|
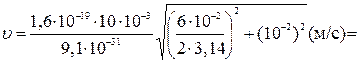
Ответ: Т = 3,57 нс,  = 24,6 Мм/с.
= 24,6 Мм/с.
Пример № 10. Катушка, содержащая N = 1000 витков, равномерно вращается с частотой n = 10 с-1 относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям индукции однородного магнитного поля (В = 0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол α = 60° с линиями поля. Площадь катушки S = 100 см2.
| Дано: | Решение: |
| N = 1000 n = 10 с-1 В = 0,04 Тл α = 60° S = 100 см2 = 10-2 м2 | По закону Фарадея-Ленца: 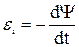 .
Потокосцепление .
Потокосцепление 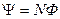 , где N – число витков катушки, пронизываемых магнитным потоком Ф.
Тогда получим: , где N – число витков катушки, пронизываемых магнитным потоком Ф.
Тогда получим: 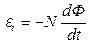 . Магнитный поток, пронизывающий катушку в момент времени t, определяется по закону . Магнитный поток, пронизывающий катушку в момент времени t, определяется по закону 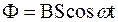 , где ω – угловая скорость вращения катушки ( , где ω – угловая скорость вращения катушки ( 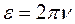 ). ).
|
| ei-? |
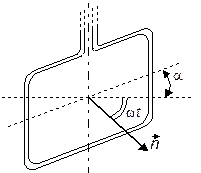 Мгновенное значение ЭДС индукции:
Мгновенное значение ЭДС индукции: 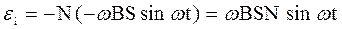 . Если учесть, что угол
. Если учесть, что угол 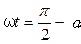 (рисунок), а
(рисунок), а 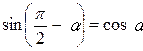 , то получим:
, то получим: 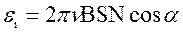 . Проведем вычисления:
. Проведем вычисления:
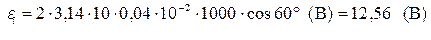
Ответ: εi =12,56 В.
1.3. Базовые задачи для самостоятельного решения
1. Как надо изменить расстояние между двумя одинаковыми точечными зарядами, чтобы при перемещении их из воздуха в масло с относительной диэлектрической проницаемостью 2 сила взаимодействия уменьшилась в 8 раз?
Ответ: r1/r2= 2
2. Шарик массой 2 г, имеющий заряд 50 нКл, подвешен в воздухе на тонкой изолирующей нити. Определите натяжение нити, если снизу на расстоянии 5 см расположен заряд -100 нКл.
Ответ: FH = 0,038 Н
3. Напряженность поля в некоторой точке равна 15 кН/Кл. Сила, действующая на некоторый заряд в этой точке, равна 3,75 ∙ 10–5 Н. На сколько надо изменить значение заряда, чтобы сила, действующая на него в этой точке, возросла в 3 раза?
Ответ:Δq = 50 нКл
4. Электрон влетает в однородное поле плоского конденсатора по направлению линий напряженности и на пути в 2 см уменьшает скорость с 2 ∙ 106 м/с до нуля. Определите напряженность поля в плоском конденсаторе.
Ответ:Е = 569 Н/Кл.
5. Воздушный конденсатор, состоящий из двух пластин площадью 10 см2, находящихся на расстоянии 2 см, поместили и керосин. На сколько надо раздвинуть пластины, чтобы емкость конденсатора не изменилась? Диэлектрическая проницаемость керосина равна 2,1.
Ответ:Δd=2,2 cм.
6. Определите плотность тока, если известно, что за 10 с через поперечное сечение проводника прошло 100 Кл электричества. Диаметр проводника 0,5 мм.
Ответ:j = 5,3∙104 А/м2.
7. Определите сопротивление медной проволоки, масса которой 1 кг, а площадь поперечного сечения 0,1 мм2.
Ответ:R=197 Ом
8. Электрическое поле создается двумя зарядами q1=4мкКл и q2= –2 мкКл, находящимся на расстоянии a=0,1 м друг от друга. Определить работу А1-2 сил поля по перемещению заряда q=50 нКл из точки 1 в точку 2.
Ответ:А1-2 = 14,3 мДж
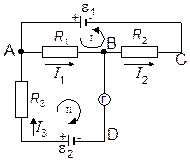 9. Определить ЭДС
9. Определить ЭДС 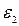 второго элемента в цепи (рисунок), если
второго элемента в цепи (рисунок), если 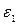 =2 В, R1=100 Ом, R2=50 Ом, R3=20 Ом. Гальванометр регистрирует силу тока I3=50 мА, идущего в направлении, указанном стрелкой. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
=2 В, R1=100 Ом, R2=50 Ом, R3=20 Ом. Гальванометр регистрирует силу тока I3=50 мА, идущего в направлении, указанном стрелкой. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
Ответ: 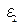 = 4 В.
= 4 В.
10. Батарея состоит из n=5 последовательно соединенных элементов, каждый с ЭДС 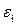 =1,4 В и внутренним сопротивлением ri=0,3 Ом. При каком токе полезная мощность батареи Рn=8 Вт? Найти наибольшую полезную мощность батареи.
=1,4 В и внутренним сопротивлением ri=0,3 Ом. При каком токе полезная мощность батареи Рn=8 Вт? Найти наибольшую полезную мощность батареи.
Ответ:I1 = 2,7 А; I2 = 2 А; Рn max = 8,2 Вт.
11. Протоны влетают со скоростью 1 км/с в однородное магнитное поле под углом 60° к линиям индукции. Величина индукции магнитного поля 1 мТл. Определите, сколько оборотов сделает протон за 0,1 с движения и какой путь в направлении линий индукции при этом пройдет протон?
Ответ:s = 50 м.
12. По тонкому проволочному кольцу течёт ток 2А. Не изменяя силы тока, проводнику придали форму квадрата. Во сколько раз изменилась индукция магнитного поля в центре контура.
Ответ: 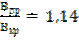 .
.
13. Протон, прошедший ускоряющую разность потенциалов U=600В, влетел в однородное магнитное поле с индукцией В=0,3Тл и начал двигаться по окружности. Определить радиус R окружности.
Ответ: 12мм.
14. Определить частоту ν обращения электрона по круговой орбите в магнитном поле с индукцией B=1Тл.
Ответ: 2,8 1010с-1.
15. Проводник длиной ℓ =20 см перемещается в однородном магнитном поле с индукцией B=0,1 Tл так, что его ось составляет угол σ=30  с направлением поля. С каким ускорением нужно двигать проводник, чтоб разность потенциалов на его концах возрастала равномерно на 1 В, за 1с.
с направлением поля. С каким ускорением нужно двигать проводник, чтоб разность потенциалов на его концах возрастала равномерно на 1 В, за 1с.
Ответ: а=100 м/с2
16. В катушке без сердечника за 0,01с ток возрастает от 1 до 2А, при этом в катушке возникает ЭДС самоиндукции, равна 20В. Найти индуктивность катушки и изменение энергии магнитного поля.
Ответ:L=0,02 Гн; ΔW=0,03 Дж.
17. По двум длинным прямолинейным проводникам, расположенным на расстоянии 10 см друг от друга течет в противоположных направлениях ток I1= 20 A и I2 = 30 A . Найти напряженность магнитного поля в точке, лежащей на расстоянии 2 см от первого проводника с током.
Ответ: Н=119,4 А/м.
18. Найти магнитный поток Ф, создаваемый соленоидом с сечением S=10см2, если он имеет n=10 витков на каждый сантиметр его длины при силе тока I=20А.
Ответ: 25,2мкВб.
19. Найти кинетическую энергию протона, движущегося по дуге окружности радиусом R=60см в магнитном поле с индукцией В=1Тл.
Ответ: 17,ЗМэВ.
20. Квадратная рамка со стороной в 40 см из эластичной проволоки находится в магнитном поле с индукцией 1 Тл. Плоскость рамки перпендикулярна вектору магнитной индукции. Рамку берут за два противоположных угла и стягивают в двойной прямолинейный провод. Определите величину электродвижущей силы индукции, возникающей в рамке, если деформация рамки происходит за 0,5 с.
Ответ:ε = 0,32 В.
1.4. Контрольные вопросы
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Решение | | | Закон Кулона и принцип суперпозиции. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |