
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Еліпс і його застосування
З еліпсом людині доводиться мати справу в найрізноманітніших галузях її діяльності. Садівник розмічає клумбу, обмежену еліпсом. Художник викреслює еліптичний контур для розпису стін або стелі зали. Математик розраховує еліптичну траєкторію руху супутника Землі. Нарешті, сама Земля, як відомо, рухається по еліпсу, в одному з фокусів якого знаходиться Сонце.
 1. Канонічне рівняння еліпса. Однією з найбільш відомих і цікавих кривих другого порядку є еліпс. Уявлення про цю криву можна отримати, напри-клад, якщо трохи стиснути круглий тонкий металевий обруч (рис.3.2). Дамо тепер строге визначення еліпса.
1. Канонічне рівняння еліпса. Однією з найбільш відомих і цікавих кривих другого порядку є еліпс. Уявлення про цю криву можна отримати, напри-клад, якщо трохи стиснути круглий тонкий металевий обруч (рис.3.2). Дамо тепер строге визначення еліпса.
Еліпсом називається множина всіх точок площини, сума відстаней від кожної з яких до двох даних точок тієї ж площини, які називаються фокусами, є величина постійна, більша, ніж відстань між фокусами.
Складемо рівняння еліпса з фокусами у точках 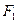 і
і  .
.
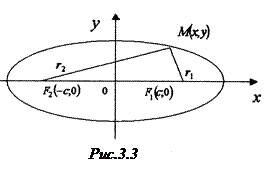 Для цього обираємо прямокутну систему координат так, щоб вісь
Для цього обираємо прямокутну систему координат так, щоб вісь  проходила через фокуси, а початок координат ділив відрізок
проходила через фокуси, а початок координат ділив відрізок 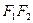 навпіл (рис.3.3).
навпіл (рис.3.3).
Позначимо  . Отримаємо
. Отримаємо  і
і  . Нехай
. Нехай  – довільна точка еліпса.
– довільна точка еліпса.
Відстані  і
і 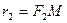 називаються фокальними радіусами точки
називаються фокальними радіусами точки 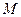 .
.
Нехай 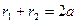 (1), тоді згідно означення еліпса
(1), тоді згідно означення еліпса 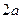 – величина постійна, причому
– величина постійна, причому 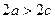 , тобто
, тобто  .
.
За формулою відстані між двома точками знаходимо
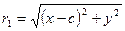 і
і  . (2)
. (2)
Підставимо знайдені значення  і
і  у рівність (1), отримаємо рівняння еліпса:
у рівність (1), отримаємо рівняння еліпса:
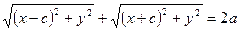 . (3)
. (3)
Перетворимо рівняння (3):
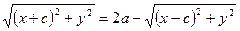 ;
;
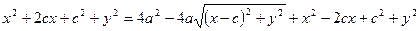 ;
;
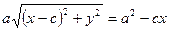 ;
;
 ;
;
тобто 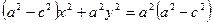 .
.
Так як  , то
, то  . Нехай
. Нехай  (4), тоді останнє рівняння прийме вигляд
(4), тоді останнє рівняння прийме вигляд 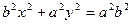 , або
, або 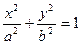 . (5)
. (5)
Рівняння (5) називається канонічним рівнянням еліпса.
Рівняння (5) є алгебраїчним рівнянням другого степеня. Отже, еліпс є алгебраїчною лінією другого порядку.
 2. Дослідження форми еліпса за його рівнянням. Визначимо форму еліпса за його канонічним рівнян-ням (рис.3.4):
2. Дослідження форми еліпса за його рівнянням. Визначимо форму еліпса за його канонічним рівнян-ням (рис.3.4):
1) Координати точки 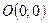 не задовольняють рівняння (5), тому еліпс, визначений цим рівнянням, не проходить через початок координат.
не задовольняють рівняння (5), тому еліпс, визначений цим рівнянням, не проходить через початок координат.
2) Знайдемо точки перетину еліпса з осями координат. Поклавши у (5) 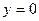 , знайдемо
, знайдемо  . Отже, вісь
. Отже, вісь  еліпс перетинає у точках
еліпс перетинає у точках 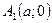 і
і 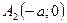 . Поклавши у (5)
. Поклавши у (5) 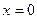 , знайдемо
, знайдемо 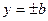 . Отже, вісь
. Отже, вісь  еліпс перетинає у точках
еліпс перетинає у точках  і
і  .
.
3) Так як у (5)  і
і 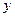 у парних степенях, то еліпс симетричний відносно координатних осей, а, отже, і відносно початку координат.
у парних степенях, то еліпс симетричний відносно координатних осей, а, отже, і відносно початку координат.
4) Всі точки еліпса знаходяться всередині прямокутника, обмеженого прямими  ,
,  ,
,  ,
, 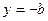 .
.
Точки 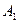 ,
, 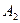 ,
,  ,
, 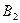 перетину еліпса з осями координат називаються вершинами еліпса.
перетину еліпса з осями координат називаються вершинами еліпса.
З (4) випливає, що 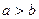 . Відрізок
. Відрізок  (
( 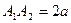 ,
, 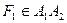 і
і  ) називається великою віссю еліпса, а відрізок
) називається великою віссю еліпса, а відрізок 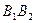 (
( 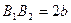 ) – малою віссю.
) – малою віссю.
Вісі  і
і 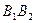 є осями симетрії еліпса, а точка
є осями симетрії еліпса, а точка 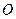 – центром симетрії (або просто центром) еліпса.
– центром симетрії (або просто центром) еліпса.
Приклад 1. Визначити довжини осей і координати фокусів еліпса 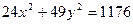 .
.
Розв’язання. Розділимо обидві частини рівняння на 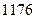 , тоді
, тоді 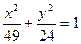 .
.
Звідси 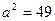 або
або 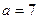 , тобто
, тобто 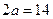 ;
;
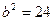 або
або 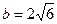 , тобто
, тобто 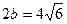 .
.
Маємо 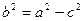 , звідки
, звідки
 .
.
Отже, координати фокусів будуть  і
і 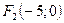 .
.
Відповідь: 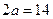 ,
, 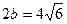 ;
;  і
і 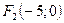 .
.
Приклад 2. Скласти канонічне рівняння еліпса, якщо фокусна відстань дорівнює 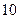 , а мала вісь дорівнює
, а мала вісь дорівнює 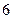 .
.
Розв’язання. Маємо 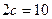 , тобто
, тобто  ;
;
 , тобто
, тобто 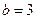 .
.
 Тоді
Тоді 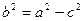 ,
,
 .
.
Отже, рівняння еліпса має вигляд 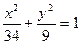 .
.
Відповідь: 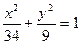 .
.
Якщо  , то рівняння (5) вже не є канонічним рівнянням еліпса. Проте і в цьому випадку (5) визначає еліпс (рис.3.5), більша вісь якого
, то рівняння (5) вже не є канонічним рівнянням еліпса. Проте і в цьому випадку (5) визначає еліпс (рис.3.5), більша вісь якого 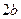 лежить на осі
лежить на осі  , а мала вісь
, а мала вісь 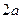 – на осі
– на осі  . Фокуси такого еліпса знаходяться в точках
. Фокуси такого еліпса знаходяться в точках  і
і  , де
, де 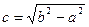 (рис.3.5).
(рис.3.5).
3. Ексцентриситет еліпса. Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини більшої осі.
Позначається ексцентриситет  .
.
Тоді:
1) 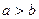 , то
, то 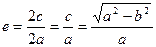 ; (6)
; (6)
2)  , то
, то 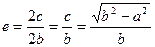 . (7)
. (7)
З формул (6) і (7) випливає, що 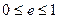 . При цьому зі збільшенням різниці між півосями
. При цьому зі збільшенням різниці між півосями  і
і 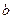 збільшується відповідним чином і ексцентриситет еліпса, наближаючись до одиниці; при зменшенні різниці між
збільшується відповідним чином і ексцентриситет еліпса, наближаючись до одиниці; при зменшенні різниці між  і
і 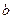 зменшується і ексцентриситет, наближаючись до нуля.
зменшується і ексцентриситет, наближаючись до нуля.
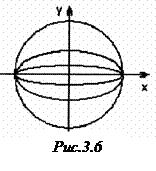 Отже, за величиною ексцентриси-тету можна судити про форму еліпса: чим більший ексцентриситет, тим більше витягнутий еліпс вздовж більшої осі; чим менший ексцен-триситет, тим більше еліпс за формою ближчий до кола (рис.3.6).
Отже, за величиною ексцентриси-тету можна судити про форму еліпса: чим більший ексцентриситет, тим більше витягнутий еліпс вздовж більшої осі; чим менший ексцен-триситет, тим більше еліпс за формою ближчий до кола (рис.3.6).
Якщо  , то
, то 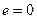 , і рівняння еліпса приймає вигляд
, і рівняння еліпса приймає вигляд  , яке визначає коло радіуса
, яке визначає коло радіуса  з центром у початку координат.
з центром у початку координат.
Отже, коло можна розглядати як частинний випадок еліпса, у якого півосі рівні між собою, а отже, ексцентриситет дорівнює нулю.
Приклад. Скласти рівняння еліпса, фокуси якого лежать на осі  , якщо його більша вісь дорівнює
, якщо його більша вісь дорівнює 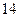 , а
, а  .
.
Розв’язання. Так як фокуси лежать на осі  , то
, то  , тобто
, тобто  , і
, і  , звідки
, звідки  . Знаходимо
. Знаходимо 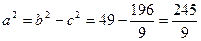 .
.
Отже, 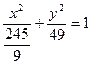 , або
, або  .
.
Відповідь:  .
.
4. Директриси еліпса. Директрисами еліпса називаються дві прямі, які перпендикулярні до осі, на якій розміщені фокуси еліпса і знаходяться на відстані  від центра еліпса.
від центра еліпса.
Директриси не перетинають сам еліпс.
Якщо фокуси лежать на осі  , то директриси еліпса паралельні осі
, то директриси еліпса паралельні осі  (рис.3.7). Тому рівняння директрис мають вигляд
(рис.3.7). Тому рівняння директрис мають вигляд 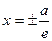 .
.
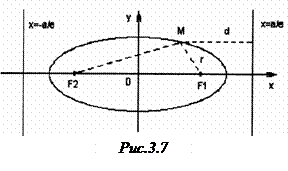 Властивість еліп-са:
Властивість еліп-са:
Відношення дов-жини фокального радіуса  кожної точки еліпса до відстані
кожної точки еліпса до відстані 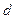 цієї точ-ки від відповідної директриси є ста-лим і дорівнює ексцентриситету еліпса, тобто
цієї точ-ки від відповідної директриси є ста-лим і дорівнює ексцентриситету еліпса, тобто 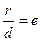 .
.
Приклад. Скласти канонічне рівняння еліпса, якщо задана точка  еліпса, а відстань між його директрисами дорівнює
еліпса, а відстань між його директрисами дорівнює 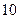 .
.
Розв’язання. Точка  лежить на еліпсі. Тому її координати задовольняють рівняння еліпса, тобто
лежить на еліпсі. Тому її координати задовольняють рівняння еліпса, тобто 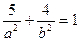 або
або 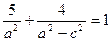 , оскільки
, оскільки 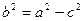 .
.
Тоді  .
.
За умовою відстань між директрисами 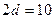 , тобто
, тобто 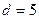 .
.
Враховуючи рівняння директриси, маємо 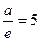 або
або  (бо
(бо  ), звідки
), звідки 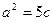 .
.
Отже, для знаходження 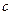 маємо рівняння
маємо рівняння
 , або
, або 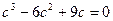 ,
,
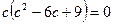 .
.
Оскільки 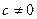 , то
, то  ,
,  ,
,  .
.
Тоді  ,
, 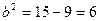 і шукане рівняння має вигляд
і шукане рівняння має вигляд  .
.
Відповідь:  .
.
5. Рівняння еліпса зі зміщеним центром. При розв’язуванні різних задач доводиться мати справу з еліпсами, центри яких не лежать в початку координат.
Якщо осі еліпса паралельні до осей координат, а центр еліпса міститься в точці  , то рівняння еліпса має вигляд
, то рівняння еліпса має вигляд
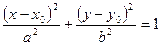 .
.
Його називають рівнянням еліпса зі зміщеним центром.
Приклад. Встановити, чи рівняння  визначає еліпс, і знайти координати його центра
визначає еліпс, і знайти координати його центра 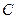 , півосі і ексцентриситет.
, півосі і ексцентриситет.
Розв’язання. Згрупуємо члени рівняння з  та
та 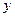 і виділимо повні квадрати. Маємо
і виділимо повні квадрати. Маємо
 ,
,
або 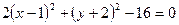 .
.
Поділимо всі члени рівняння на 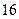 :
:
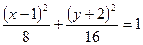 .
.
Це рівняння еліпса. Центр еліпса знаходиться в точці 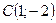 , мала піввісь дорівнює
, мала піввісь дорівнює 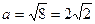 , а велика –
, а велика –  .
.
Оскільки велика вісь міститься на прямій, паралельній  , то
, то 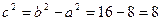 , тобто
, тобто  .
.
Тоді 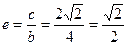 .
.
Відповідь: еліпс, 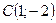 ,
,  ,
, 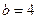 ,
, 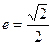 .
.
6. Застосування еліпса до розв’язування прикладних задач. Наведемо «оптичну» властивість еліпса:
Промінь світла, що посилають з точкового джерела, яке розміщене у фокусі еліпса, відобразившись від еліпса як від дзеркальної поверхні, потрапляє у другий фокус.
Згідно одному з законів Кеплер, кожна планета Сонячної системи рухається еліптичною траекторією, в одному з фокусів якої знаходиться Сонце. Також еліптичними траекторіями обертаються навколо Землі тисячі штучних супутників.
Приклад. Земля рухається по еліпсу, в одному з фокусів якого знаходиться Сонце. Найменша відстань Землі від Сонця дорівнює приблизно 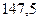 млн. км, а найбільша –
млн. км, а найбільша – 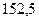 млн. км. Знайти більшу піввісь і ексцентриситет орбіти Землі.
млн. км. Знайти більшу піввісь і ексцентриситет орбіти Землі.
Розв’язання. Більша вісь орбіти Землі дорівнює сумі найменшої та найбільшої її відстаней від Сонця, тобто 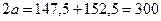 млн. км.
млн. км.
Отже, більша піввісь орбіти Землі дорівнює 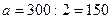 млн. км.
млн. км.
Знайдемо фокусну відстань орбіти Землі. Для цього знайдемо різницю більшої осі та подвоєної найменшої відстані Землі від Сонця:
 млн. км.
млн. км.
Знайдемо ексцентриситет:  .
.
Відповідь: більша піввісь  млн. км, ексцентриситет
млн. км, ексцентриситет  .
.
Контрольні питання
1) Дати означення еліпса.
2) Яке канонічне рівняння еліпса?
3) Що називають вершинами еліпса? Які їх координати?
4) Скільки осей симетрії має еліпс? Як вони розташовані?
5) Що називається великою і малою осями еліпса?
6) Що називається ексцентриситетом еліпса? Записати формулу для обчислення ексцентриситету.
7) Як ексцентриситет характеризує форму еліпса?
8) Що називають директрисами еліпса? Записати їх рівняння.
9) Записати рівняння еліпса зі зміщеним центром.
10) Розказати про практичне застосування еліпса.
Читайте також:
- V. Виконання вправ на застосування узагальнювальних правил.
- А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
- Автомобільні ваги із застосуванням цифрових датчиків
- Акти застосування норм права в механізмі правового регулювання.
- Акти застосування юридичних норм: поняття, ознаки, види.
- Акти правозастосування, їх види
- Акти правозастосування.
- Алгоритм із застосування річної процентної ставки r.
- Алгоритм із застосуванням річної облікової ставки d.
- Аміноглікозиди (стрептоміцину сульфат, гентаміцину сульфат). Механізм і спектр протимікробної дії, застосування, побічні ефекти.
- Аналіз зображувальних засобів. Застосування цілісного аналізу
- Антисептики ароматичного ряду (фенол чистий, іхтіол, дьоготь, мазь Вількінсона, лінімент за Вишневським). Особливості протимікробної дії та застосування.
| <== попередня сторінка | | | наступна сторінка ==> |
| Відповіді | | | Практичні завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |