
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Дисперсія системи функцій випадкових величин
Якщо маємо систему декількох нелінійних функцій системи випадкових величин (Х1, Х2, ..., Хп )
Y = f(Х) = 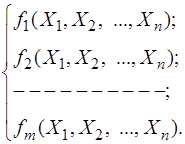 , (3.60)
, (3.60)
то спочатку їх приводять до лінійного виду.
Розклавши в ряд систему функцій (3.60) отримаємо систему лінійних функцій:
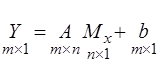 , (3.61)
, (3.61)
де 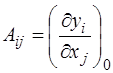 за умови Х = Х0.
за умови Х = Х0.
Математичним сподіванням системи випадкових функцій Мy системи випадкових величин (Х1, Х2, ..., Хп )за аналогією з формулою (3.52) буде
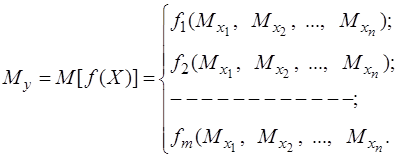 , (3.62)
, (3.62)
де 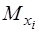 визначається за формулами (2.15 – 2.17).
визначається за формулами (2.15 – 2.17).
Дисперсією системи випадкових функцій Dy системи випадкових величин (Х1, Х2, ..., Хп)є кореляційна матриця функцій випадкових величинKy. В матричному вигляді маємо
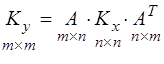 . (3.63)
. (3.63)
В розкритому вигляді матриці елементів формули (3.63) будуть
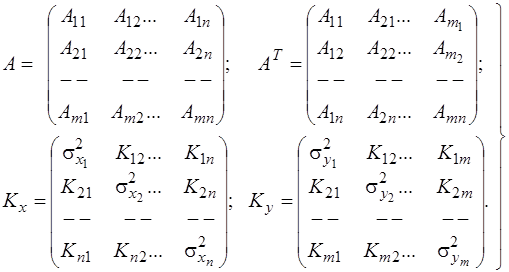 . (3.64)
. (3.64)
Причому, якщо в матриці Ky кореляційні моменти Kijвизначають залежність між випадковими величинами аргументів Хіі Хj, то в матриці Ky кореляційні моменти Kij визначають залежність між випадковими функціями Yi і Yj. Величину коефіцієнта кореляції між випадковими функціями Yi і Yj обчислюють за формулою
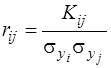 . (3.65)
. (3.65)
Приклад 1. Випадкові величини Х та Y пов’язані відношенням
z = x + 2xy + 2y – 1.Ймовірність появи кожної із них однакова, а реалізації приведені в табл.3.1.
Таблиця 3.1
| Ном. | |||||
| хі | 5,0 | 5,2 | 4,8 | 5,1 | 4,9 |
| уі | 1,0 | 0,8 | 1,2 | 0,6 | 1.4 |
Необхідно визначити: а) математичні сподівання, дисперсії і стандарти випадкових величин Хі Y; б) кореляційну матрицю Kx і нормовану матрицю 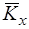 системи випадкових величин (X); в) математичне сподівання, дисперсію і стандарт випадкової функції Y.
системи випадкових величин (X); в) математичне сподівання, дисперсію і стандарт випадкової функції Y.
Розвязання. а) Для визначення математичних сподівань випадкових величин Хі Y використаємо формулу (2.16). Так як ймовірність появи випадкових величин однакова, а число їх N = 5, то ймовірність появи кожної із них в дослідженнях буде дорівнювати
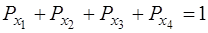 , а
, а 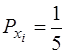 =0,2;
=0,2;
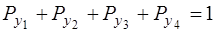 , а
, а 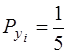 =0,2.
=0,2.
Розрахунки виконані виходячи з того, що сума ймовірностей складає повну групу подій. Тоді за формулою (2.16) маємо
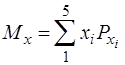 =(5,0 + 5,2 + 4,8 + 5,1 + 4,9) 0,2 = 5,0;
=(5,0 + 5,2 + 4,8 + 5,1 + 4,9) 0,2 = 5,0;
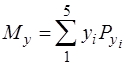 = (1,0 + 0,8 + 1,2 + 0,6 + 0,4) 0,2 = 1,0.
= (1,0 + 0,8 + 1,2 + 0,6 + 0,4) 0,2 = 1,0.
Дисперсії випадкових величин обчислюють за формулою (2.27). Так як 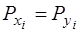 = 0,2, то дисперсії дорівнюють:
= 0,2, то дисперсії дорівнюють:
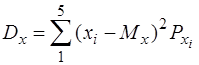 = [02 + (0,2)2 + (-0,2)2 + (0,1)2 + (-0,1)2]0,2 = 0,02;
= [02 + (0,2)2 + (-0,2)2 + (0,1)2 + (-0,1)2]0,2 = 0,02;
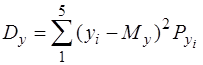 = [02 + (-0,2)2 + (0,2)2 + (-0,4)2 + (0,4)2]0,2 = 0,08.
= [02 + (-0,2)2 + (0,2)2 + (-0,4)2 + (0,4)2]0,2 = 0,08.
Стандарти будуть дорівнювати:
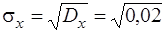 = 0,14;
= 0,14;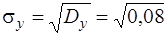 =0,26.
=0,26.
б) Для визначення кореляційної матриці Kx обчислимо кореляційний момент між випадковими величинами ХіY за формулою (3.22). Так як 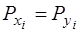 = 0,2, то
= 0,2, то 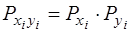 = 0,2 × 0,2 = 0,04.
= 0,2 × 0,2 = 0,04.
Тоді
Kху = Kух = [0× 0 + 0,2 × (-0,2) + (-0,2) × 0,2 + 0,1 × (-0,4) + (-0,1)×0,4] ´ 0,04 = 0,0064.
Кореляційна матриця Kx згідно з формулою (3.34) буде
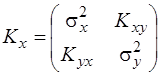 =
= 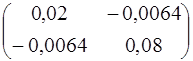 .
.
За формулою (3.37) обчислимо коефіцієнт кореляції
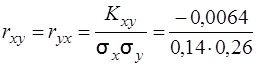 = -0,12.
= -0,12.
Нормована кореляційна матриця 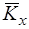 за формулою (3.38) буде
за формулою (3.38) буде
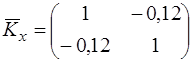 .
.
в) Математичне сподівання випадкової функції Z згідно з формулами (3.48) і (3.49) буде
Mz = Mx + 2Mx My + 2 My – 1 – Kxy = 5 + 2×5×1 + 2×1 – 1 – 0,0064 = 15,9936.
Дисперсію випадкової функції Z обчислимо за формулою (3.57)
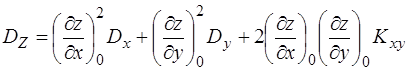 =
=
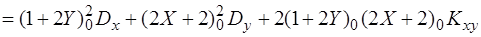 .
.
При Х0 = Мx ; Y0 = My
DZ = (1 + 2× 1)2 0,02 + (2× 5 + 2)2 0,08 + 2 (1 + 2 × 1) (2 × 5 + 2)´(- 0,0064) = 11,53.
Тоді стандарт функції Zбуде
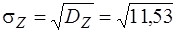 = 3,36.
= 3,36.
Приклад 2. На пункті полігонометрії способом кругових прийомів виміряні кути у1, у2 і у3(рис.3.4). Найти кореляційну матрицю Кy, коефіцієнт кореляції між кутами rij і дисперсію кута у4 = у1 + у2, якщо
 виміряні напрямки х1, х2, х3,х4незалежні між собою, а їх стандарт дорівнює
виміряні напрямки х1, х2, х3,х4незалежні між собою, а їх стандарт дорівнює 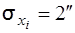 .
.
Рис.3.4
Розв’язання. Так як кути обчислюються через значення виміряних напрямків, то складемо вектор-функцію (3.60):
у = f(x) = 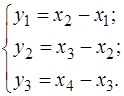
Кореляційна матриця обчислюється за формулою (3.63). Коефіцієнти матриці A обчислюються як часткові похідні Аij = 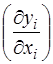 , так А11 = -1; А12 = + 1 і т.д.
, так А11 = -1; А12 = + 1 і т.д.
Тоді
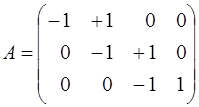 .
.
Виходячи з того, що виміри рівноточні і незалежні між собою, то за формулою (3.36) кореляційна матриця 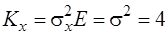 .
.
За формулою (3.63) обчислимо кореляційну матрицю Ky
Ky =А s2 АТ = 4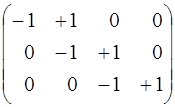
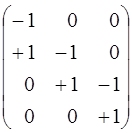 =
=
=4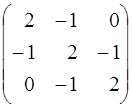 =
= 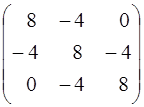 .
.
По діагоналі розміщені дисперсії кутів. Причому вони рівноточні, так як 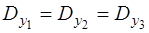 = 8. Тоді стандарт кута
= 8. Тоді стандарт кута 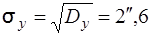 .
.
Із отриманої матриці Kyвидно, що спостерігається залежність тільки між суміжними кутами, так як
K12 = K23 = - 4, а K13 = 0.
Коефіцієнти кореляції між суміжними кутами у1 і у2; у2 і у3 обчислюють за формулою (3.65)
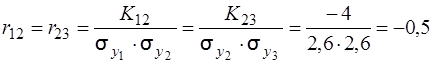 .
.
Це означає, що в способі кругових прийомів, залежність між суміжними кутами завжди дорівнює rij = -0,5; (j = i + 1) або (i = j +1).
Дисперсія кута у4 обчислюється за формулою (3.57) або (3.58) і дорівнює
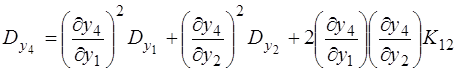 .
.
Так як 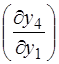 = + 1 і
= + 1 і 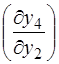 = + 1,
= + 1,
то 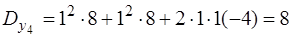 ,
,
а дисперсія сумарного кута буде
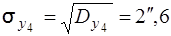 .
.
§ 6. Граничні теореми теорії ймовірностей
Теорія ймовірностей охоплює питання передбачення результату того чи іншого явища або експерименту. Якщо явище є одиничним, то можна визначити ймовірність кінцевого результату в досить широких межах. Якщо явище є масовим, що виникає в подібних умовах, то при достатньо великій кількості досліджень випадкові події і випадкові величини стають майже невипадковими. Це дозволяє використовувати результати досліджень над випадковими явищами для передбачення результатів майбутніх досліджень.
Теореми, які встановлюють співвідношення між теоретичними і експериментальними характеристиками випадкових величин і випадкових подій при досить великій кількості досліджень, а також розглядають граничні закони їх розподілу називають граничними теоремами теорії ймовірностей. Серед них найбільш важливе значення мають граничні теореми: закон великих чисел та центральна гранична теорема.
Закон великих чиселдозволяє знайти зв’язок між теорією ймовірностей і закономірностями масових випадкових явищ, і має досить велике практичне значення.
Важливою формою закону великих чисел єтеорема П.Л.Чебишова, що встановлює зв’язок між можливим емпіричним середнім арифметичним значенням хвипадкової величини Х і її математичним сподіванням Мx.
Її формулюють так: при необмеженому збільшенні числа незалежних випробувань середнє арифметичне спостережених значень випадкової величини, що має кінцеву дисперсію, збігається за ймовірністю до її математичного сподівання.
Теорема П.Л. Чебишова цілком справедлива і при застосуванні в теорії математичної обробки геодезичних вимірів. За умовами цієї теореми на випадкові величини Х1, Х2, ..., Хп накладають обмеження:
1) вони повинні мати однакові математичні сподівання, тобто
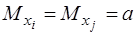 ,
,
де а– істинне значення випадкової величини Х;
2) їх дисперсії не повинні перевищувати наперед відомого додатного числа С: 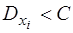 (
( 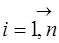 );
);
3) вони повинні бути попарно незалежними, тобто будь-яке хі і хjпри і ¹ j незалежні.
В цьому випадку яке б не було б додатне (плюсове) число x при п ® ¥
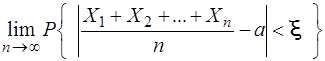 = 1.(3.66)
= 1.(3.66)
Це твердження доводиться на основі нерівності Чебишова: ймовірність того, що відхилення випадкової величини від її математичного сподівання буде за абсолютною величиною не менше будь-якого додатного (плюсового) числа x, обмежена зверху величиною 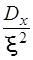 , тобто
, тобто
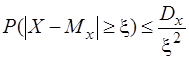 . (3.67)
. (3.67)
Якщо в формулі (3.66) випадкові величини Х1, Х2, ..., Хп замінити на центровані величини 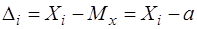 , то отримаємо
, то отримаємо
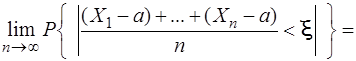
= 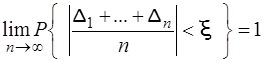 (3.68)
(3.68)
Це означає, що середнє арифметичне великої кількості відхилень випадкових центрованих величин, від їх математичного сподівання за умови, що 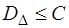 і п ® ¥збігається за ймовірністю до нуля.
і п ® ¥збігається за ймовірністю до нуля.
Таким чином, закон великих чисел виявляє як статистичні властивості, так і умови визначення середнього значення випадкової величини.
Досить велике значення в практиці має центральна гранична теорема А.М.Ляпунова.Вона виявляє умови, при яких виникає нормальний закон розподілу. Якщо випадкова величина Х відповідає вимогам:
1) вона є сумою достатньо великої кількості інших незалежних величин Х1, Х2, ..., Хп (п ® ¥ ) ;
2) випадкові величини попарно незалежні, тобто Хі і Хj незалежні при і ¹ j;
3) відхилення випадкових величин від своїх математичних сподівань не перевищує досить малої величини в порівнянні з відхиленнями сумарної величини, тобто Хі - 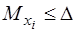 .
.
Граничний закон розподілу для суми визначиться за формулою
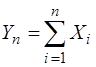 . (3.69)
. (3.69)
Тоді,згідно з теоремою А.М.Ляпунова: Якщо випадкові величини Х1, Х2, ..., Хпвзаємно незалежні, мають один і той же закон розподілу з математичним сподіваннямМxі дисперсієюDx при необмеженому збільшенні їх числа, закон розподілу величин Y(формула 3.69) необмежено наближається до нормального.
В той же час, випадкові величини Х1, Х2, ..., Хп можуть мати довільний розподіл імовірностей. Згідно з теоремою Муавра-Лапласа, якщо всі випадкові величини Хіоднаково розподілені, дискретні і приймають тільки два можливих значення 0 чи 1, то це передбачає окремий випадок центральної граничної теореми.
Теорема Муавра-Лапласа описує поведінку біноміального розподілу при великих значеннях п. При цьому обчислення ймовірності попадання випадкової величини Yв інтервал (α,b),що визначається за формулою
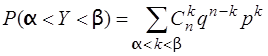 , (3.70)
, (3.70)
може виконуватися за формулою
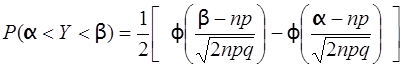 , (3.71)
, (3.71)
де q = 1 – p, p– ймовірність появи події в кожному із досліджень.
Збіжність закону розподілу випадкової величини Y до нормального забезпечується за умови
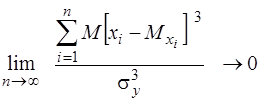 .
.
Розробку і доведення центральної граничної теореми виконали П.Лаплас та А.М.Ляпунов. Великий внесок зробили П.Л.Чебишов, А.А.Марков, С.Н.Бернштейн, А.Я.Хинчин, А.П.Колмогоров, Б.В.Гнеденко та інші.
Запитання для самоперевірки
1. Що називають системою випадкових величин?
2. Дайте визначення функції розподілу системи двох випадкових величин і покажіть їх властивості.
3. Як визначити ймовірність попадання випадкової точки в задану область?
4. Дайте визначення щільності розподілу системи випадкових величин та назвіть її властивості.
5. Які випадкові величини називають залежними та незалежними?
6. Назвіть види залежностей між випадковими величинами.
7. Приведіть функцію та графік щільності нормального розподілу двох випадкових величин.
8. Які числові характеристики двомірної випадкової величини?
9. Що називається кореляційним моментом та коефіцієнтом кореляції?
10. Приведіть формули кореляційного моменту та коефіцієнта кореляції для системи двох дискретних випадкових величин.
11. Які випадкові величини називають некорельованими?
12. Чи витікає із некорельованості випадкових величин їх незалежність і навпаки?
13. Що називають функцією розподілу системи п-випадкових величин?
14. Як визначається щільність розподілу системи п-випадкових величин?
15. За допомогою яких числових характеристик характеризують систему п-випадкових величин?
16. Що називають кореляційною матрицею системи п-випадкових величин?
17. Яка матриця називається нормованою кореляційною матрицею?
18. При яких умовах виникає діагональна матриця?
19. Що можна сказати про закон розподілу функції випадкових величин?
20. Як визначається математичне сподівання функції випадкових величин?
21. Чому дорівнює математичне сподівання суми та добутку випадкових величин?
22. Як визначається дисперсія функції випадкових величин?
23. Приведіть формулу для дисперсії функції некорельованих випадкових величин.
24. Запишіть систему декількох функцій системи випадкових величин.
25. Запишіть у загальному вигляді математичне сподівання системи декількох функцій системи випадкових величин.
26. Напишить формулу кореляційної матриці функцій випадкових величин.
27. Як визначити коефіцієнти матриць А і Kx ?
28. Яка сутність законy великих чисел?
29. Сформулюйте теорему Чебишова.
30. Які обмеження накладаються на випадкові величини в теоремі Чебишова?
31. Яка сутність центральної граничної теореми Ляпунова?
32. При яких умовах виникає нормальний закон розподілу випадкових величин?
Читайте також:
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
- IV. Розподіл нервової системи
- IV. Система зв’язків всередині центральної нервової системи
- IV. Філогенез кровоносної системи
- POS-системи
- T. Сутність, етіологія та патогенез порушень опорно-рухової системи
- VI. Філогенез нервової системи
- А) Заробітна плата її форми та системи.
- А) Заробітна плата, її форми та системи.
- А) оптимальне значення величини зварювального струму; б) підвищене значення величини зварювального струму; в) низьке значення величини зварювального струму.
| <== попередня сторінка | | | наступна сторінка ==> |
| Дисперсія функції випадкових величин | | | Сутність і функції податків. Податкова система. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |