
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Пояснення
1. Знайдемо горизонтальні проекції точок А, В, В1, які знаходяться на бічній поверхні конуса обертання.
Через проекцію А2 (т. А) проведемо паралель і визначимо її радіус (R), який проводять відносно осі і на П1 та за проекційним зв’язком знаходять проекцію т. А1. Через проекції В2, В21 т. В, В1 проведемо твірні (твірна проходить через вершину конуса до перетину з його основою). На побудованих горизонтальних проекціях цих твірних фіксуємо положення проекцій В1 та В11.

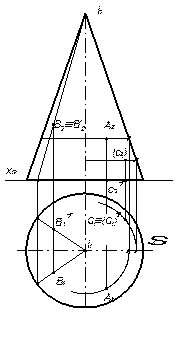
Рисунок 73 – Циліндр обертання Рисунок 74 – Конус обертання
Знайдемо фронтальні проекції т. С, С1. З рис. 74 видно, що т. С належить бічній поверхні конуса, а т. С1 – основі. Тому проекція С21 т. С1 фіксується безпосередньо за проекційним зв’язком (на фронтальній проекції основи конуса), а С2 знаходимо аналогічно побудові для точки А, тобто за допомогою паралелі.
Оскільки т. С знаходиться за проекцією головного меридіана (див. слід-проекцію Σ1), то на П2 вона невидима.
Приклад 3. Для конічної поверхні (рис. 75) з однією напрямною запишіть визначник поверхні та вкажіть на яких лініях знаходиться т. С та т. D.

Рисунок 75 – Конічна поверхня
Відповіді:
1. Визначник поверхні: Ø (l, m, S) ,
|
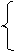
 l – твірна;
l – твірна;
|
|
S – вершина. l∩m.
2. D Ì m (належить напрямній), C Ì l (належить твірній).
Приклад 4. Для заданих поверхонь запишіть їх визначник та вкажіть, які точки кожної з поверхонь належать обрисовим твірним на П1та П2 (рис. 76, рис. 77).
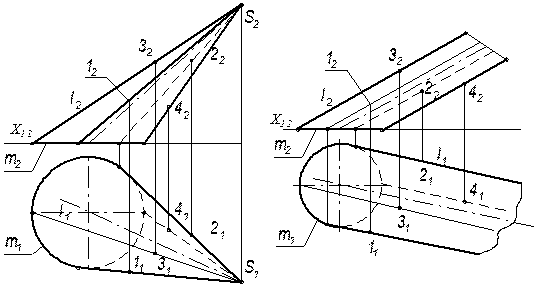
Рисунок 76 – Конус загального Рисунок 77 – Циліндр загального
положення положення.
Відповіді:
1) Визначники у поверхонь такі:
( m, l, S ) – конус загального ( m, l ) – циліндр загального
положення, положення,
|
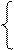
 m – напрямна, коло; m – напрямна, коло;
m – напрямна, коло; m – напрямна, коло;
ГЧ l – твірна, пряма; ГЧ l – твірна, пряма.
S – вершина.
 |
 l∩li=S, l׀׀li,
l∩li=S, l׀׀li,
АЧ l∩m, АЧ l∩m,
m׀׀П1. l׀׀П1
2) На обрисових твірних заданих поверхнях в П2 знаходяться точки 3 та 4; на обрисових твірних в П1 – точки 1 та 2.
Приклад 5. Дайте назву та запишіть визначник показаної поверхні (рис. 78).
Відповіді:
1. Поверхня, що показана на рис. 78, має назву – косий відкритий гелікоїд або гвинтовий циліндроїд.
2. Визначник поверхні:

Ø (m, n, l, l’, i),

|
l – твірна;
l′ – твірна напрямного конуса;
i – вісь гелікоїда.
 l׀׀l′;
l׀׀l′;
l∩m, n,
(l−n);
i ┴П1.
Рисунок 78 - Косий відкритий коноїд
9.5 Теоретичні питання
1. Дайте означення кривої лінії. Відміни між плоскою та просторовою кривою.
2. В чому різниця між закономірною та незакономірною кривими?
3. Як утворюється циліндрична та конічна гвинтові лінії. Що таке крок гвинтової лінії?
4. Які способи задання поверхонь на кресленні вам відомі?
5. Що називають каркасом, обрисом поверхні?
6. Дайте поняття визначника поверхні. Складові частини визначника.
7. Як утворюються поверхні обертання? Визначник поверхні.
8. Як побудувати на поверхні обертання паралель, меридіан, головний меридіан?
9. Які окремі види поверхонь обертання вам відомі?
10. Як утворюються поверхні переносу? Визначник поверхні.
11. Які поверхні називають лінійчастими? Скільки напрямних можуть
мати лінійчасті поверхні?
12. Скільки напрямних мають поверхні Каталана? Визначник поверхні.
13. Як утворюються гвинтові поверхні? Визначник поверхні. Скільки
напрямних мають гвинтові поверхні?
14. За якою ознакою гвинтові поверхні поділяють на відкриті та закриті?
15. Наведіть приклади застосування кривих поверхонь в науці та техніці.
Читайте також:
- V. Пояснення нового матеріалу
- V.Пояснення нового матеріалу
- Від них необхідні відомості, документацію і пояснення з питань охоро1
- Відповіді та пояснення до розв’язання задач
- ЕФЕКТ КОМПТОНА І ЙОГО ПОЯСНЕННЯ
- Е_4. Пояснення і прогнозування моделей
- Засоби доказування Пояснення сторін і третіх осіб
- ІV. Пояснення вчителя.
- ІV. Пояснення нового матеріалу
- ІІІ. Пояснення нового матеріалу.
- Методи герменевтики пояснення та розуміння дійсності
- Парадокс Леонтьєва та його пояснення
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклади для закріплення | | | Задачі для самостійної підготовки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |