
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Закони розподілу випадкових величин
При обробці великих об’ємів статистичних даних головним важливим питанням є встановлення законів розподілу тих чи інших випадкових величин. Математичний вираз, що дає зв'язок між можливим значенням випадкової величини і ймовірністю їх появи, називають законом розподілу випадкових величин
Розподіл дискретних випадкових величин характеризують ймовірністю їх появи. Якщо при проведені 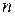 дослідів із них в
дослідів із них в 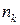 величина х прийняла значення
величина х прийняла значення 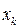 то ймовірністю появи значення
то ймовірністю появи значення 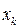 називається величина
називається величина  . Очевидно, що
. Очевидно, що 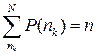
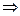
 - умова нормування.
- умова нормування.
Таким чином найбільш простою формою задання закону розподілу дискретної величини є вказання можливих величин ймовірності кожного із отриманих значень 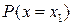 ,
, 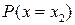 ,
, 
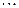
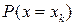 . Тобто розподіл дискретної випадкової величини повністю визначається за допомогою наступної таблиці:
. Тобто розподіл дискретної випадкової величини повністю визначається за допомогою наступної таблиці:
| Значення вимірюваної величини, х | 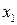
| 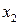
| 
| 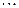
| 
|
| Імовірність її появи, Р | 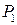
| 
| 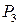
| 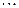
| 
|
У випадку неперервних випадкових величин ймовірність виявити серед кінцевого набору числових значень якесь наперед задане число практично рівна нулю. Тоді більш змістовним будуть питання , скільки вимірюваних значень  лежить в певному інтервалі від
лежить в певному інтервалі від 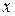 до
до  , яка ймовірність того що випадкова величина прийме значення, менше наперед заданого значення
, яка ймовірність того що випадкова величина прийме значення, менше наперед заданого значення 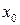 , або яка імовірність того що випадкова величина знаходиться в інтервалі від
, або яка імовірність того що випадкова величина знаходиться в інтервалі від 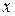 до
до  .
.
Ймовірність того що випадкова величина прийме значення, менше наперед заданого значення  являється деякою функцією
являється деякою функцією  :
:
 .
.
Ця функція  називається функцією розподілу ймовірності випадкової величини або інтегральною функцією розподілу.
називається функцією розподілу ймовірності випадкової величини або інтегральною функцією розподілу.
Визначимо ймовірність події, яка полягає в тому, що значення вимірюваної величини попадає в інтервал 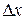 . Припустимо, що проведено n вимірювань деякої випадкової величини x: x1, x2, ... xn – одним і тим же методом і з однаковою ретельністю. Можна очікувати, що число
. Припустимо, що проведено n вимірювань деякої випадкової величини x: x1, x2, ... xn – одним і тим же методом і з однаковою ретельністю. Можна очікувати, що число 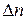 отриманих результатів, які лежать в деякому достатньо вузькому інтервалі від
отриманих результатів, які лежать в деякому достатньо вузькому інтервалі від 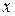 до
до  , повинно бути пропорційне:
, повинно бути пропорційне:
- величині даного інтервалу 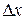 ;
;
- загальному числу вимірювань 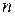 .
.
Таким чином, можна записати, що  , де f (x) - функція, що характеризує розподіл значень випадкових величин по різних інтервалах. Імовірність Р(x) того, що деяке значення
, де f (x) - функція, що характеризує розподіл значень випадкових величин по різних інтервалах. Імовірність Р(x) того, що деяке значення 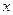 лежить в інтервалі від
лежить в інтервалі від 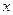 до
до  , визначається наступним чином
, визначається наступним чином
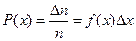 .
.
Функція f(х) називається функцією розподілу густини ймовірності випадкової величини. Із приведеної вище формули слідує, що
 .
.
Як постулат теорії похибок приймається, що результати вимірювань і їх випадкові похибки при великій їх кількості підкоряються закону нормального розподілу.
Читайте також:
- I. Доповнення до параграфу про точкову оцінку параметрів розподілу
- IV. Закони ідеальних газів.
- VII розділ. Маркетингові рішення з розподілу та збуту товару
- А) Грошовий обіг. Закони.
- А) оптимальне значення величини зварювального струму; б) підвищене значення величини зварювального струму; в) низьке значення величини зварювального струму.
- Абсолютна величина дійсного числа
- Абсолютна величина можливих значень
- Абсолютна величина числа позначається символом .
- Абсолютні величини
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
- Абсолютні, відносні та середні величини.
| <== попередня сторінка | | | наступна сторінка ==> |
| Параметри статистичних розподілів | | | Емпіричний закон розподілу густини ймовірності неперервної випадкової величини |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |