
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Скалярний добуток двох векторів
Означення 3.6.1. Скалярним добутком 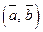 двох ненульових векторів
двох ненульових векторів  та
та 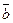 називається число, яке дорівнює добутку довжин векторів, що перемножуються, на косинус кута між ними:
називається число, яке дорівнює добутку довжин векторів, що перемножуються, на косинус кута між ними:
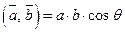 .
.
Якщо хоча б один з векторів  або
або 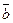 є нульовим, тоді вважають
є нульовим, тоді вважають 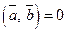 . Іноді для скалярного добутку
. Іноді для скалярного добутку 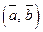 користуються іншим позначенням:
користуються іншим позначенням: 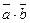 . З означення скалярного добутку двох векторів випливають наступні його властивості.
. З означення скалярного добутку двох векторів випливають наступні його властивості.
Властивість 1.Скалярний добуток 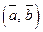 комутативний. Для будь-яких векторів
комутативний. Для будь-яких векторів  та
та 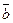 :
:
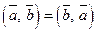 .
.
Властивість 2. Скалярний добуток довільного вектора  на себе дорівнює квадрату довжини цього вектора:
на себе дорівнює квадрату довжини цього вектора:
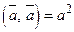 .
.
Відзначимо, що скалярний добуток 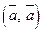 прийнято називати скалярним квадратом вектора
прийнято називати скалярним квадратом вектора  та позначати:
та позначати: 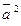 . Внаслідок властивості 2 скалярного добутку
. Внаслідок властивості 2 скалярного добутку
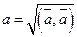 .
.
Властивість 3. Для будь-яких векторів  та
та 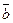 :
: 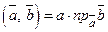 , якщо
, якщо 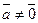 .
.
4 За теоремою 3.5.4 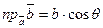 . Помножимо обидві частини цієї рівності на модуль вектора
. Помножимо обидві частини цієї рівності на модуль вектора  , одержимо
, одержимо
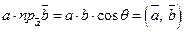 .3
.3
Таким чином, 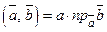 . Очевидно, при
. Очевидно, при 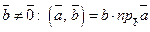 .
.
Властивість 4. Для будь-яких векторів  та
та 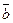 та для будь-якого дійсного
та для будь-якого дійсного 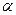 вірні рівності
вірні рівності
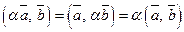 .
.
4 Якщо один з векторів  або
або 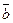 є нульовим, то твердження теореми справедливо. Нехай
є нульовим, то твердження теореми справедливо. Нехай  та
та 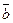 ненульові вектори, тоді за властивістю 3 скалярного добутку та за теоремою 3.5.3 (властивість проекцій) маємо
ненульові вектори, тоді за властивістю 3 скалярного добутку та за теоремою 3.5.3 (властивість проекцій) маємо
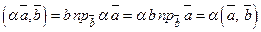 .
.
У силу комутативності скалярного добутку: 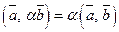 .3
.3
Властивість 5. Якщо 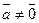 та
та 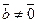 – довільні ненульові вектори та
– довільні ненульові вектори та 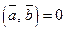 , то
, то  та
та 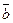 – ортогональні.
– ортогональні.
4 Нехай 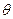 – кут між векторами
– кут між векторами  та
та 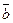 . За умовою
. За умовою 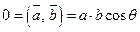 . Оскільки
. Оскільки 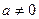 і
і 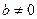 , то
, то 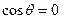 . В області
. В області 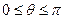 функція
функція 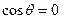 лише при
лише при 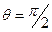 . Отже, вектори
. Отже, вектори  і
і 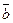 ортогональні. 3
ортогональні. 3
Властивість 6. Для будь-яких векторів 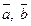 та
та 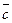 :
:
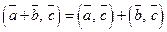 .
.
4 При 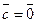 зазначена рівність виконується. Нехай
зазначена рівність виконується. Нехай 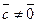 , тоді за властивістю 3 скалярного добутку векторів
, тоді за властивістю 3 скалярного добутку векторів 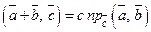 . За теоремою 3.5.2:
. За теоремою 3.5.2: 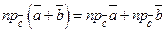 , тому
, тому 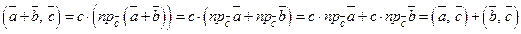 .3
.3
Наслідок. Для будь-яких векторів 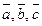 та
та 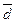 :
: 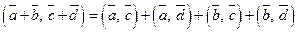 .
.
У § 3.4 було показано, що будь-які три некомпланарні вектори можуть утворювати базис у тривимірному векторному просторі.
Означення 3.6.2.Якщо базисні вектори 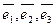 – одиничні (довжини дорівнюють одиниці) та попарно ортогональні, то базис
– одиничні (довжини дорівнюють одиниці) та попарно ортогональні, то базис 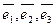 називається ортонормованим.
називається ортонормованим.
Ортонормований базис може бути правим або лівим.
Означення 3.6.3.Відкладаємо вектори 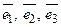 ортонормованого базису з однієї точки О простору. Будемо прагнути, повертаючи вектор
ортонормованого базису з однієї точки О простору. Будемо прагнути, повертаючи вектор 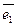 навколо точки О у площині векторів
навколо точки О у площині векторів 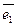 і
і 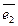 сполучити його з вектором
сполучити його з вектором 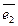 . Із двох напрямків обертання варто обрати той, якому відповідає найменший кут повороту. Якщо для спостерігача, що дивиться з кінця вектора
. Із двох напрямків обертання варто обрати той, якому відповідає найменший кут повороту. Якщо для спостерігача, що дивиться з кінця вектора 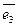 на площину векторів
на площину векторів 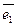 і
і 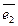 , зазначений поворот вектора
, зазначений поворот вектора 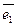 відбувається проти ходу годинникової стрілки, то базис
відбувається проти ходу годинникової стрілки, то базис 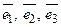 вважається правим. У супротивному випадку базис
вважається правим. У супротивному випадку базис 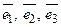 – лівий. На малюнках зображені правий і лівий ортонормовані базиси.
– лівий. На малюнках зображені правий і лівий ортонормовані базиси.
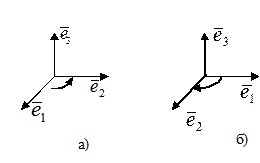
Рис.3.5. а) Правий базис Рис.3.5. б) Лівий базис
Надалі, говорячи про ортонормований базис тривимірного векторного простору, будемо завжди вважати, що базис є правим. Легко переконатися у тому, що базис 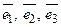 є ортонормованим тоді й тільки тоді, коли мають місце рівності
є ортонормованим тоді й тільки тоді, коли мають місце рівності
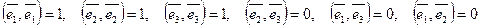 . (6.1)
. (6.1)
Розглянемо тепер кілька завдань, з якими доводиться часто зустрічатися під час розв’язування практичних і теоретичних питань векторної алгебри.
Формула для обчислення скалярного добутку векторів,
| <== попередня сторінка | | | наступна сторінка ==> |
| Проекція вектора на вісь | | | Які задані своїми координатами в ортонормованому базисі |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |