
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Табличний запис ЗЛП. Алгоритм СМ для ЗЛП, представлених в симетричній формі.
Розглянемо ЗЛП, представлену в симетричній формі: знайти найбільше значення функції
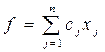 (1.20)
(1.20)
при обмеженнях
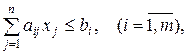 (1.21)
(1.21)
 (1.22)
(1.22)
Ввівши змінні 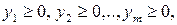 з (1.21) отримаємо
з (1.21) отримаємо
 (1.23)
(1.23)
Подамо дану задачу у вигляді, зручному для запису в симплексну таблицю, а саме:
 (1.24)
(1.24)
Звідси випливає, що розв’язок 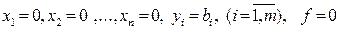
є опорним для даної задачі. Будемо покращувати його, користуючись методом повного виключення змінних (метод Жордана-Гаусса). Нагадаємо, що при цьому одночасно вирішується питання про сумісність системи обмежень та наявність у ній неістотних обмежень, тобто рівнянь, які є лінійними комбінаціями інших. Надалі систему обмежень задачі будемо вважати сумісною, а всі її рівняння – лінійно незалежними. Запишемо вихідні дані задачі в симплексну таблицю 1.2.
Таблиця 1.2
| –x1 | –x2 | … | –xn | ||
| y1 | a11 | a12 | … | a1n | b1 |
| y2 | a21 | a22 | … | a2n | b2 |
| … | … | … | … | … | … |
| ym | am1 | am2 | … | amn | bm |
| f | –c1 | –c2 | … | –cn |
Перш ніж приступити до знаходження оптимального плану, зробимо декілька зауважень.
Зауваження 1.3. Якщо в симплексній таблиці, яка містить деякий опорний план, всі елементи f–рядка (не рахуючи вільного члена) невід’ємні, то цей опорний план є оптимальним.
Зауваження 1.4. Якщо в f–рядку симплексної таблиці, яка містить деякий опорний план, є хоча б один від’ємний елемент (не рахуючи вільного члена), якому відповідає стовпчик з хоча б одним додатнім елементом, то можна, перетворивши базис, перейти до другого опорного плану з більшим значенням цільової функції.
Зауваження 1.5. Якщо в f–рядку симплексної таблиці, яка містить деякий опорний план, є хоча б один від’ємний елемент, якому відповідає стовпчик недодатних елементів
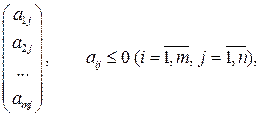
то цільова функція необмежена на множині планів, тобто 
Зауваження 1.6. Якщо в f–рядку симплексної таблиці, яка містить оптимальний план, є хоча б один нульовий елемент (не рахуючи вільного члена), то ЗЛП має нескінченну множину оптимальних планів.
Дамо коротку характеристику алгоритму знаходження оптимального плану.
Змінну, яку вводять в базис, визначають від’ємним елементом f-рядка. Якщо в f-рядку декілька від’ємних елементів, в базис буде вводитися змінна  яка відповідає від’ємному елементу
яка відповідає від’ємному елементу  з найбільшою абсолютною величиною. Тоді стовпчик коефіцієнтів
з найбільшою абсолютною величиною. Тоді стовпчик коефіцієнтів  при змінній
при змінній 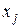 , яка включається в базис, називається розв’язуючим стовпчиком.
, яка включається в базис, називається розв’язуючим стовпчиком.
Таким чином, вибираючи змінну, яка вводиться в базис, за від’ємним елементом f-рядка, ми забезпечуємо зростання функції f .
Для знаходження змінної  яку виключають з базису, утворюють відношення вільних членів до додатних елементів розв’язуючого стовпчика і знаходять серед них найменше, яке і визначає розв’язуючий рядок, що містить змінну
яку виключають з базису, утворюють відношення вільних членів до додатних елементів розв’язуючого стовпчика і знаходять серед них найменше, яке і визначає розв’язуючий рядок, що містить змінну  :
:

Визначення 1.16 Елемент, який знаходиться на перетині розв’язуючого рядка і розв’язуючого стовпця, називається розв’язуючим елементом.
Перехід до нового базису називається симплексним перетворенням. В результаті цієї операції відбувається перерозподіл ролей між двома змінними, які входять в деяку систему лінійних рівнянь: одна змінна із залежних переходить в незалежні, а друга навпаки. Відповідний коефіцієнт f–рядка 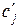 стане невід’ємним. Така операція відома в алгебрі під назвою кроку перетворень Жордана-Гаусса. Досить часто її називають кроком модифікованого виключення Жордана-Гаусса.
стане невід’ємним. Така операція відома в алгебрі під назвою кроку перетворень Жордана-Гаусса. Досить часто її називають кроком модифікованого виключення Жордана-Гаусса.
Сформулюємо правило перерахунку елементів при переході до нового опорного плану, ближчого до оптимального:
1. Розв’язуючий елемент замінюємо на обернений до нього.
2. Елементи розв’язуючого рядка ділимо на розв’язуючий елемент.
3. Елементи розв’язуючого стовпчика діляться на розв’язуючий елемент, взятий з протилежним знаком.
4.  Решта елементів знаходимо за правилом прямокутника:
Решта елементів знаходимо за правилом прямокутника:

 ,
,
де  – розв’язуючий елемент.
– розв’язуючий елемент.
Після здійснення l кроків 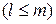 перетворень Жордана-Гаусса ми одержимо наступну симплексну таблицю 1.3.
перетворень Жордана-Гаусса ми одержимо наступну симплексну таблицю 1.3.
Таблиця 1.3
| –у1 | –у2 | … | –ym | –xm+1 | … | –xn | ||
| х1 | b11 | b12 | … | b1m | b1m+1 | … | b1n | a1 |
| х2 | b21 | b22 | … | b2m | b2m+1 | … | b2n | a2 |
| … | … | … | … | … | … | … | … | … |
| хm | bm1 | bm2 | … | bmm | bmm+1 | … | bmn | am |
| f | q1 | q2 | … | qm | qm+1 | … | qn | Q |
Оскільки в таблиці усі  , то розв’язок буде оптимальним. Для його одержання потрібно небазисні (ті, які розташовані зверху симплексної таблиці) змінні вважати рівними нулю. Тоді базисні змінні будуть дорівнювати вільним членам
, то розв’язок буде оптимальним. Для його одержання потрібно небазисні (ті, які розташовані зверху симплексної таблиці) змінні вважати рівними нулю. Тоді базисні змінні будуть дорівнювати вільним членам 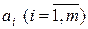 і
і 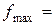 Q.
Q.
Знову повертаємося до прикладу 1.1. Запишемо (1.11) та (1.14) у вигляді, зручному для запису у симплексну таблицю
 (1.25)
(1.25)
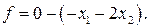 (1.26)
(1.26)
| і яка матиме вигляд: | –x1 | –x2 | ||
| y1 | ||||
| y2 |  1 1
| |||
| y3 | ||||
| f | –1 | –2 | ||
| |
Візьмемо в (1.25) і (1.26) 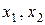 рівними нулю, одержимо
рівними нулю, одержимо 
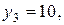
 . Даний розв’язок є опорним. Його можна покращити за рахунок збільшення змінної
. Даний розв’язок є опорним. Його можна покращити за рахунок збільшення змінної  (їй відповідає найбільший за модулем від’ємний коефіцієнт в
(їй відповідає найбільший за модулем від’ємний коефіцієнт в 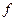 -рядку). Відповідний стовпчик буде розв’язуючим. Оскільки
-рядку). Відповідний стовпчик буде розв’язуючим. Оскільки 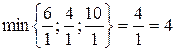 , то, розв’язуючим є другий рядок. Число 1, яке лежить на перетині другого рядка і другого стовпця, буде розв’язуючим елементом. Провівши для нього один крок перетворень Жордана–Гаусса, прийдемо до наступної таблиці:
, то, розв’язуючим є другий рядок. Число 1, яке лежить на перетині другого рядка і другого стовпця, буде розв’язуючим елементом. Провівши для нього один крок перетворень Жордана–Гаусса, прийдемо до наступної таблиці:
| –x1 | –у2 | ||
| y1 |  1 1
| –1 | |
| х2 | |||
| y3 | –1 | ||
| f | –1 |
Отриманий розв’язок:  не є оптимальним, оскільки в
не є оптимальним, оскільки в 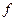 -рядку є від’ємний елемент. Розв’язок можна покращити за рахунок збільшення змінної
-рядку є від’ємний елемент. Розв’язок можна покращити за рахунок збільшення змінної  (їй відповідає від’ємний коефіцієнт в
(їй відповідає від’ємний коефіцієнт в 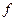 -рядку). Як і раніше, знаходимо
-рядку). Як і раніше, знаходимо 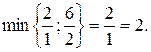 Тому перший рядок розв’язуючий, а 1 – розв’язуючий елемент. Провівши один крок перетворень Жордана-Гаусса, одержимо:
Тому перший рядок розв’язуючий, а 1 – розв’язуючий елемент. Провівши один крок перетворень Жордана-Гаусса, одержимо:
| –у1 | –у2 | ||
| х1 | –1 | ||
| х2 | |||
| y3 | –2 | ||
| f |
Розв’язок  є оптимальним, оскільки в
є оптимальним, оскільки в 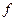 -рядку відсутні від’ємні елементи.
-рядку відсутні від’ємні елементи.
Читайте також:
- Rete-алгоритм
- Алгоритм
- Алгоритм
- Алгоритм 1.
- Алгоритм 2
- Алгоритм RLE
- Алгоритм безпосередньої заміни
- Алгоритм Берлекемпа-Мессі
- Алгоритм відшукання оптимального плану.
- Алгоритм Гоморі
- Алгоритм Дейкстри.
- Алгоритм Деккера.
| <== попередня сторінка | | | наступна сторінка ==> |
| Алгоритм СМ у формі тотожних перетворень | | | Алгоритм СМ для ЗЛП, представлених в загальному виді |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |