Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

В-84 Дифракція електронів на одномірному кристалі

Мета: ознайомитись із особливостями дифракції електронів під час взаємодії пучка частинок із кристалічною ґраткою та навчитись визначати за допомогою отриманих експериментальних даних параметри кристалу і елементарних частинок.

Прилади і матеріали: комп’ютерна програма “Дифракція електронів”.

Теоретичні відомості

Для вивчення атомної будови кристалів використовують дифракцію та розсіяння рентгенівського випромінювання, електронів і нейтронів. Розвиток струк-турного аналізу почався від появи праці М. Лауе (1912 р.). Лауе показав, що коли пучок рентгенівського випромінювання проходить через кристал, то відбувається дифракція, причому розподіл дифракційних максимумів точно відповідає симетрії кристала. Це зумовлено тим, що звичайний тривимірний кристал з періодичною структурою представляє собою дифракційну решітку для рентгенівського випромінювання, оскільки його довжина хвиль порівнянна з міжатомною відстанню d в кристалах. Дифракційні максимуми виникають у тих напрямах, які задовольняють умову Вульфа - Брегга

2d sin θ = nλ, (84.1)

тобто лише для певних напрямів і міжплощинних відстаней.

Основні методи рентгеноструктурного аналізу кристалів залежно від умов реєстрації дифракційної картини поділяються на дві групи: 1) кут падіння променів на кристал постійний, змінюється довжина хвилі; 2) довжина хвилі постійна, а змінюється кут падіння. Для цих двох видів і фіксується дифракційна картина, що задовольняє умовуВульфа - Брегга.

До першого методу належить метод Лауе. На кристал, орієнтований під певним кутом до рентгенівського випромінювання, падає пучок такого немоноенергетичного йонізуючого випромінювання. Через неперервність спектра рентгенівського випромінювання лише ті хвилі, які задовольняють умову (84.1), дифрагуватимуть. В результаті на фотопластинці за кристалом утвориться дифракційна картина, симетричне розташування темних плям.

За положенням цих плям визначають форму і розмір елементарної комірки. Вимірюючи інтенсивності (кількісно) дифрагованих променів, можна визначити розташування атомів в елементарній комірці. Чим різкіші і чіткіші плями спостерігаються на фотопластинці, тим структура кристалічної решітки ідеальніша. Якщо плями і розмиті і широкі, то це означає, що в кристалі існують певні порушення решітки, структурні дефекти та інші відхилення від ідеальності. Отже, метод Лауе досить просто дає інформацію про структурну досконалість або недосконалість кристалів.

Для другого методу можливі два випадки.

Метод обертання. Використовується моноенергетичне йонізуюче рентгенівське випромінювання, а кристал повертається навколо осі кристалографічної зони перпендикулярно до падаючого пучка. Різні площини кристала послідовно займають положення, що відповідає умові дифракції.

Метод порошку (метод Дебая-Шеррера) полягає в тому, що полікристал або дрібний порошок з монокристалічних зерен освітлюється монохроматичним пучком. Із безлічі різнорідних мікрокристаликів завжди знайдуться такі, орієнтація яких задовольняє умову дифракції.

На основі експериментальних результатів за дифракційною картиною можна зробити висновок про геометрію решітки, а за інтенсивністю дифракції — про розподіл атомів у комірці. Інтенсивність дифракційних максимумів вимірюється за ступенем почорніння фотопластинки або за допомогою електронних методів. Можна її виміряти і за допомогою автоматичних дифрактометрів. За відносною інтенсивністю дифракційних максимумів визначається розподіл електронної густини, тобто ймовірність знаходження електронів в тій чи іншій точці решітки.

Зазначимо ще, що за інтенсивністю розсіяння рентгенівського випромінювання в кристалі визначають швидкості поширення пружних хвиль, анізотропію і пружні модулі, спектр пружних коливань. Останнім часом методи рентгеноструктурного аналізу широко використовуються для дослідження структури реальних кристалів.

Для дослідження структури тонких плівок (на пропускання) і поверхневих шарів (на відбивання) використовується дифракція електронів. Можна досліджувати процес росту кристалів, структуру тонких плівок, вплив окислення на структуру поверхні і, нарешті, природу процесів полірування і мащення.

Енергію, яку повинен мати електрон, щоб дифракційні ефекти мали місце, знаходять із співвідношення де Бройля:

λ= h/mv, (84.2)

де т і v – маса і швидкість частинки.

Для того щоб довжина хвилі була порядку атомних відстаней у кристалах, різниця потенціалів V має бути близько 150 В:

λ = 12,25/ . (84.3)

Тут λвиражається в нанометрах, а V — у вольтах.

До установки для вивчення дифракції електронів входять: вакуумна камера, електронна пушка, держак зразка (плівок) і фотопластинка або флуоресціюючий екран для реєстрації картини дифракції.

Для дослідження структури кристалів використовується також дифракція нейтронів. Нейтрони розсіюються в основному ядрами і незначно електронами, за винятком тих випадків, коли електрони неспарені і створюють навколо атомів магнітне поле, оскільки нейтрон має магнітний момент і розсіюється магнітним полем неспарених електронів. Це дає змогу визначити ймовірність розподілу неспарених електронів у кристалах, а також напрям магнітних дипольних моментів відносно осей кристала.

Завдяки наявності у нейтронів магнітного моменту вони взаємодіють з “магнітними” електронами твердого тіла; тому використання нейтронів має велику цінність для структурного аналізу магнітних кристалів. В немагнітних матеріалах нейтрони взаємодіють з ядрами атомів, що утворюють ґратку.

Метод дифракції нейтронів виявився дуже корисним для визначення локалізації окремих атомів (наприклад, атомів водню) у молекулах і є більш точним, ніж рентгенівський метод.

Таким чином, дифракційні методи - це сьогодні основні експериментальні методи дослідження структури твердих тіл.

Сучасна фізика трактує всі матеріальні об’єкти як такі, що володіють подвійною природою, адже вони проявляють як хвильові, так і корпускулярні властивості.

Найбільш яскраво хвильові властивості проявляються у мікрооб’єктів (елементарних частинок). Адже внаслідок малої маси m довжина хвилі де Бройля для них виявляється близькою з міжатомними відстанями в кристалах. А це означає, що кристали стають для цих об’єктів потенційними дифракційними ґратками. Тобто під час взаємодії з кристалічною ґраткою спрямованого на неї пучка елементарних частинок будуть спостерігатись дифракційні явища.

Якщо пучок таких електронів спрямувати на кристал, то вони будуть розсіюватись за законами дифракції. Але для цього електрони повинні володіти енергією біля 100 еВ (пройти різницю потенціалів ≈ 100 В і досягнути швидкості ≈ 10⁷ м/с), щоб довжина хвилі де Бройля дорівнювала б ≈ 10^-10 м. Адже такого порядку є міжатомні відстані в кристалах. Зафіксована на фотопластинці дифракційна картина називається електронограмою. Вона містить інформацію про будову, дефекти та інші особливості тривимірної кристалічної ґратки.

Оскільки електрони є зарядженими частинками, вони сильно взаємодіють з речовиною. Тобто глибина їх проникнення в кристал порівняно невелика. Тому структурне дослідження методом дифракції електронів найбільш суттєве (ефективне) для дослідження плівок, поверхонь, дуже тонких кристалів та газів.

Моделлю розсіяння електронів на кристалах може бути мислимий експеримент із дифракції електронів на одномірній ґратці. З хвильової точки зору цей експеримент повністю еквівалентний оптичному досліду з традиційною дифракційною ґраткою. Положення головних дифракційних максимумів в цьому випадку буде визначатись формулою ґратки

, (84.4)

де d – період ґратки,

n – порядок дифракційного максимуму,

λ – довжина хвилі де Бройля (84.2),

θ_n – кут дифракції.

Для малих кутів дифракції, згідно умови малості кута, отримуємо

. (84.5)

Якщо на деякій відстані L від ґратки помістити фотопластину, то на ній буде зафіксована дифракційна картина у вигляді вузьких дифракційних смуг, положення яких x_n визначається формулою

. (84.6)

Підставляючи (84.5) у (84.6), отримаємо формулу для визначення періоду кристалічної ґратки

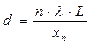. (84.7)

В квантовій фізиці розподіл інтенсивності в дифракційній картині інтерпретується як розподіл ймовірності попадання електрона в різні точки екрану. Кожний електрон взаємодіє з кристалічною ґраткою як хвиля (тобто зі всією ґраткою в цілому), але на екрані він локалізується в певній точці. Таким чином дифракційна картина на екрані виникає як результат ймовірнісного процесу.

Інтерфейс програми „Дифракція електронів”

Довжина хвилі де Бройля для електронів, прискорених різницею потенціалів U, визначається за формулою

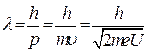, (84.8)

де m = 9,1·10^-31 кг – маса електрона, е = 1,6·10^-19 Кл – його заряд, U – прискорююча різниця потенціалів, h = 6,63·10^-34 Дж·с – стала Планка.

В комп’ютерній моделі, як видно із рисунок 84.1, можна змінювати період ґратки d і швидкість υ (за рахунок зміни прискорюючої різниці потенціалів U), яка визначає довжину хвилі де Бройля для електронів. В правій частині екрану виникає усереднений за тривалий час розподіл кількості електронів, що попадають на екран в різні точки фотопластини (див. рисунок 84.1). Цей розподіл співпадає з кривою розподілу інтенсивності світла під час дифракції на одномірній ґратці.

В центрі екрану моделюється ймовірнісний процес попадання окремих електронів на фотопластинку. Зверніть увагу, що в результаті тривалого спостереження на фотопластинці спостерігаються не тільки головні максимуми, але також і слабкі побічні максимуми дифракційної картини.

Послідовність виконання роботи

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Література	\|	Завдання 1. Ознайомлення із можливостями моделі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.