• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

НЕВИЗНАЧЕНІСТЬ ЦІЛЕЙ ТА КОМПРОМІСИ ПАРЕТО

Розділ 6. ПРИЙНЯТТЯ БАГАТОЦІЛЬОВИХ РІШЕНЬ ЗА УМОВ РИЗИКУ

Основні терміни: невизначеність цілей, множина Парето, метод нормалізації, співвідношення пріоритету, критерій згортки.

НЕВИЗНАЧЕНІСТЬ ЦІЛЕЙ ТА КОМПРОМІСИ ПАРЕТО

До цього часу розглядалися дещо спрощені випадки, коли вважалося, що певним чином обрано єдиний критерій, за яким проводять оцінку ефективності, і треба лише відшукати мак­симум (мінімум) деякого показника ефективності. На жаль, практично такі задачі зустрічаються не завжди.

Розглянемо приклад. Організується (реорганізується) під­приємство. 3а яким критерієм (функціоналом) суб'єкт керу­вання повинен обирати рішення? З одного боку, бажано було б максимізувати сподіваний валовий обсяг продукції, одер­жати максимальний інтегрований дисконтований сподіваний до­ход, мінімізувати сподівану собівартість продукції. З іншого боку, дуже бажано мати мінімальний ризик, пов'язаний з відхиленням планових результатів від тих, що реалізуються, тощо.

Для того, щоб привести задачу на прийняття рішень до стандартної задачі оптимізації, слід сформулювати додаткові гіпотези, які безпосередньо не витікають з умов задачі.

У багатокритеріальних задачах природно намагатися від­шукати способи приведення їх до задач з одним критерієм, бо для однокритеріальних задач існують добре відпрацьовані методи розв'язання будь-якої строго сформульованої математичної задачі.

У [29] розглядається багатокритеріальний метод оптимізації, запропонований Італійським економістом В. Парето.

Маємо й критеріїв f_i; 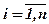. Знайдено деякий розв'язок задачі. Позначимо його через „х” і вважатимемо, що існує інший розв'язок „х”, де для усіх критеріїв „f_і(х)” мають місце нерівності:

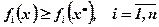; (6.1)

при цьому хоча б одна із нерівностей — строга. Очевидно, що розв'язок „х” пріоритетніший, ніж розв'язок „х*”. Тому всі вектори „х*”, що задовольняють умові (6.1), слід відразу виключити з подальшого розгляду, тобто далі є сенс аналізувати лише ті вектори „х*”, для яких не існує такого „х”, щоб виконувалась умова (6.1). Множина таких значень „х*” називається множиною Парето. Проілюструємо метод виділення паретових розв'язків на при­кладі задачі з двома критеріями f₁ та f₂ (обидва треба мак­симізувати), тобто:

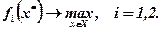(6.2)

Каждой точке 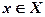соотношение:

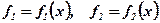(6.3)

ставлять у відповідність деяку точку в площині критеріїв (рис. 6.1). Співвідношенням (6.3) визначають відображення мно­жини X на f.

Рис. 6.1. Відображення множини X(а) на множину f(б)

Множина «f» називається множиною досягнутості чи гранич­них можливостей.

Множина Парето являє собою лише частину границі мно­жини досягнутості, тобто до неї належать ті значення критеріїв, над якими не домінують інші варіанти.

На рис. 6.1 множиною Парето буде дуга АСВ.

Опишемо одну з схем побудови множини Парето. Фіксують певні бажані значення критеріїв f₁ та f₂: f₁ = с₁, f₂ = с₂.

Величини с₁ та с₂ слід вибрати так, щоб вони належали до множини досягнутості.

Розв'язують дві оптимізаційні задачі.

I. 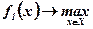; при условии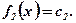

II. 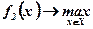; при условии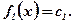

Розв'язавши ці задачі визначають точки а та b(рис. 6.2).

Якщо провести через них пряму I, отримаємо найбільш просту апроксимацію множини Парето. Для уточнення цієї апроксимації розв'язують наступні задачі III та IV і знаходять дві точки с та d, які належать цій множині:

III. 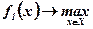; при условии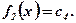

IV. 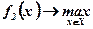; при условии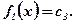

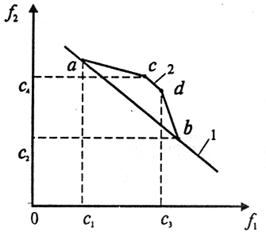
Рис. 6.2. Наближена множина Парето

Значення с₃ та с₄теж повинні належати до множини досягнутості. Через точки а, с, d, b проводять ламану 2, котра і вважається наступним наближенням. Цієї інформації про струк­туру множини Парето буває вже достатньо для розв'язку прак­тичних задач, якщо ні, то будують подальші наближення.

У [29] наведений інший спосіб апроксимації множини Па­рето. Нехай "λ₁" та "λ₂"— строго додатні числа, такі, що

λ₁ + λ₂ = 1. (6.4)

Формуємо новий критерій

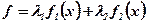(6.5)

та розв'язуємо наступну задачу математичного програмування:

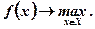(6.6)

Виявляється, що розв'язок цієї задачі визначає такий вектор „х”, що точка f₁= f₁(x), f₂= f₂(x) належить до множини Парето.

Тому апроксимацію множини Парето можна здійснити таким чином (рис. 6.3). Розв'язують задачу

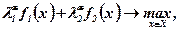(6.7)

де 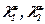задовольняють умові (6.4).

Задача (6.4), (6.7) визначить деякий вектор "λ_а", котрий у площині „f” визначить точку „α” з координатами

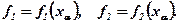
Таким самим способом визначається точка "β"; і через „α” та "β" проводять пряму 1. Вона буде першим наближенням множини Парето (рис. 6.3).

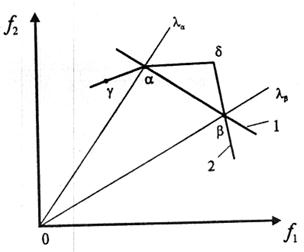
Рис. 6.3. Апроксимація множини Парето

Будуючи точки "γ" та "δ" одержують ламану 2, яка є наступним наближенням множини Парето, і т. д.

Якщо множина Парето є опуклою, то, збільшуючи кількість точок, котрі визначаються за одним з описаних вище способів, можна побудувати багатогранник, що апроксимує цю множину з будь-якою точністю. Але, на жаль, практика дає приклади множин Парето, що не є опуклими. Тоді задача їх апроксимації дуже ускладнюється.

Читайте також:

1. Альфред Маршалл, Джон Бейтс Кларк, Вільфредо Парето, Леон-Марі Еспрі Вальрас).
2. Аналіз вимог та динаміки попиту на міжнародному та внутрішньому ринку туристичних послуг (за видами туризму, за категоріями туристів, цілей та об’єктів відвідування)
3. Варіанти формулювання цілей ТНК
4. Вибір цілей реклами
5. Визначення збалансованості асортименту продукції за принципом Парето
6. Визначення потреби у підготовці персоналу, цілей навчання, розробка навчальних планів і програм
7. Визначення цілей
8. Визначення цілей формування товарних запасів.
9. Вимірювання інформації в теорії інформації (інформація, як знята невизначеність). Кількість інформації по Хартлі
10. Вимоги до організації та нормативи зберігання лікарських засобів у приміщеннях лікувально-профілактичного закладу, призначених для цих цілей
11. Вимоги до побудови «дерева цілей».
12. Вимоги до цілей

Переглядів: 844