Багатопрольотні статично визначні балки

Зміна величини поперечної сили на якій-небудь ділянці балки дорівнює площі епюри розподіленого навантаження q на цій ділянці.

Залежності між побудованими епюрами

Між епюрами М і Q і навантаженням, що діє на балку, існують визначені залежності. Ці залежності дають можливість перевіряти правильність епюр і полегшують їхню побудову. Вони вірні не тільки для балок, але і для рамних систем, а тому мають велике значення в будівельній механіці.

Основна залежність має вигляд:

Q=dM/dx (2.6)

тобто поперечна сила дорівнює першій похідній від згинального моменту по абсцисі перерізу балки (теорема Журавського).

Аналогічно між поперечною силою й інтенсивністю навантаження існує також диференціальна залежність:

Q=dQ/dx (2.7)

Враховуючи ці залежності, можна сформулювати ряд положень:

1) на ділянках, де значення моментів зменшуються (зліва направо зі спадаючими значеннями М) відповідають ділянки з від”ємними значеннями Q, а на ділянках, де значення моментів М збільшуються— ділянки з додатніми значеннями Q;

2) чим крутіше дотична до епюри М, тим більше абсолютне значення Q. Числове значення поперечної сили дорівнює «тангенсу» кута між цією дотичною і віссю балки;

3) у перерізах, де поперечна сила дорівнює нулю, згинальний момент максимальний або мінімальний;

4) між зосередженими силами (якщо між ними відсутнє розподілене навантаження) епюра М обмежена прямою (у загальному випадку похилою), а епюра Q - прямою горизонтальною лінією;

5) на ділянках балки з рівномірно розподіленим навантаженням епюра М обмежена параболою другого ступеня, а епюра Q - похилою прямою;

6) при розподіленому навантаженні епюра М звернена опуклістю в ту сторону, у яку направлене це навантаження;

7) точкам прикладення зосереджених сил, перпендикулярних до осі балки, відповідають переломи в епюрі М і скачки на епюрі Q. Якщо сила направлена вниз, то й скачок на епюрі Q при переміщенні зліва направо повинний бути вниз; коли сила направлена вверх, то і скачок повинен бути вверх; величина скачка дорівнює величині сили;

8) зміна величини згинаючого моменту на якій-небудь ділянці балки дорівнює площі епюри поперечних сил на цій ділянці (за умови, що на даній ділянці до балки не прикладені зовнішні моменти);

Серед статично визначних балочних систем важливе місце займають багатопрольотні шарнірно-консольні балки. Порівнюючи між собою статично визначні однопрольотні балки (рис. 2.3,а) і нерозрізну балку (рис. 2.3,6) під дією розподіленого і зосередженого навантажень, можна зробити висновок, що нерозрізна балка більш економічна. Дійсно, завдяки наявності опорних моментів найбільші значення згинальних моментів в нерозрізній балці, як правило, менші, ніж в однопрольотних. А саме моменти визначають розміри поперечних перерізів балки. В той же час нерозрізна балка має певні недоліки. Вона є статично невизначною і тому в ній можуть виникати додаткові зусилля при неточності виготовлення, нерівномірному осіданні опор і при нерівномірному нагріванні чи охолодженні. Якщо врахування цих особливостей веде до суттєвого збільшення витрат на зведення споруди, балку роблять статично визначною. При розстановці шарнірів по прольотах необхідно виконати вимогу геометричної незмінності. З урахуванням уніфікації окремих елементів балки в більшості застосовують два основних варіанти розстановки шарнірів, показаних на рис. 2.4,а,б, хоча можливі і інші, наприклад, на рис. 2.4,в.

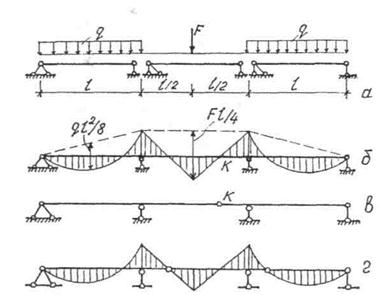
Рис.2.3

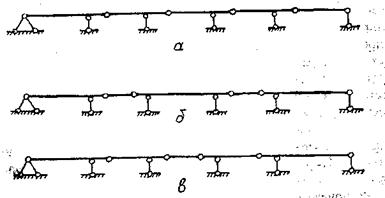
Рис. 2.4

Поставимо в якому-небудь перерізі нерозрізної балки шарнір. Тоді її ступінь статичної невизначеності зменшується на одиницю. Якщо при цьому шарнір помістити в перерізі з нульовим згинальним моментом, наприклад К (рис. 2.3.в), то розподіл згинальних моментів залишається таким же, як у вихідній балці.

Якщо кількість шарнірів прийняти рівною ступеню статичної невизначеності вихідної нерозрізної балки, то ступінь вільності отриманої балки буде рівна нулю. Така балка з шарнірами в прольотах є багатопрольотною статично визначною балкою (рис. 2.3.г). Інакше її називають шарнірно-консольною балкою. Відзначимо, що для статично визначної балки відпадає необхідність в задоволенні умов сумісності деформацій. Завдяки чому при постійному навантаженні з'являється можливість переміщенням шарнірів досягти навіть кращого розподілу згинальних моментів в порівнянні з нерозрізною балкою.

При проектуванні шарнірно-консольної балки необхідно вирішити питання про число шарнірів і їх розташування. Число шарнірів отримаємо з умови статичної визначеності балки. Враховуючи, що в балці кількість дисків завжди на одиницю більше числа з'єднувальних шарнірів, умову W= 0 можна записати:

W =3(Ш +1)-2Ш-С₀=0, звідки

Ш = С₀-3.(1.2)

Для забезпечення геометричної незмінності розташування шарнірів повинно задовольняти наступним вимогам:

- в кожному прольоті не може бути більше двох шарнірів;

- в суміжних прольотах не може знаходитись по два шарніри;

- прольоти без шарнірів не можуть знаходитись поряд;

- в крайньому прольоті при крайній шарнірній опорі не може бути більше одного шарніра;

- в крайньому прольоті при крайній защемлюючий нерухомій опорі повинен бути хоча б один шарнір.

Як правило, віддаль від шарніра до найближчої опори приймається в межах від 1/7 до 1/4 величини прольоту по умові раціонального розподілу згинальних моментів.

Шарніри ділять багатопрольотну балку на окремі елементи. Серед них виділяють основні і другорядні. Основними називають ті елементи, які залишаються геометричне незмінними при видаленні суміжних елементів. Решту елементів називають другорядними

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Порядок та методи розрахунку балок	\|	Розрахунок шарнірно-консольної балки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.