• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Правила віднімання

Правило віднімання числа від суми: «Щоб відняти число від суми, достатньо відняти його від одного з доданків та до отриманого результату додати інший доданок».

Дане правило сформулюємо символічно.

Якщо а, b, с – цілі невід’ємні числа, то:

1) при а ≥ с маємо, що (а + b) – с = (а – с) + b;

2) при b ≥ с маємо, що (а + b) – с = а + (b – с);

3) при а ≥ с та b ≥ с можемо використати будь-яку з даних рівностей.

Доведення (для випадку 1).

Нехай а ≥ с, тоді різниця а – с існує. Позначимо її буквою р, тобто а – с = р. Звідси а = р + с. Підставимо суму р + с замість а у вираз (а + b) – с та виконаємо перетворення: (а + b) – с = (р + с + b) – с = р + b. Але так як р = а – с, то (а + b) – с = = (а – с) + b, що й треба було довести.

Доведення для випадків 2 і 3 аналогічне.

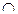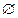Покажемо графічне зображення доведення даного правила за допомогою кругів Ейлера. Розглянемо три скінчені множини A, B та C такі, що n (A) =а, n (В) = b, n (С) = с, A B = та C 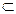A. Тоді (а + b ) – с – це кількість елементів множини (А В)\С, а число (а – с) + b – це кількість елементів множини (А\С) В. На кругах Ейлера множина (А В)\С зображена заштрихованою областю. Але множина (А\С) В зображується такою ж самою областю. Тому (А В)\С = (А\С) В для даних множин А, В і С. Отже, n ((А В)\С) = n ((А\С) В) та (а + b) – с = (а – с) + b.

Аналогічно можна показати графічне зображення для випадків 2 і 3.

Правило віднімання суми від числа: «Щоб від даного числа відняти суму, достатньо відняти від нього послідовно кожен доданок», тобто якщо а, b, с – цілі невід’ємні числа, то при а ≥ b + с маємо

а – (b + с) = (а – b) – с = (а – с) – в.

Доведення даного правила та його теоретико-множинне тлумачення за допомогою кругів Ейлера є аналогічними.

Дані правила в початковій школі розглядаються на конкретних прикладах при визначенні раціонального способу обчислення. Правило віднімання суми від числа є основою прийому віднімання по частинам:

12 – 5 = 12 – (2 + 3) = (12 – 2) – 3 = 10 – 3 = 7.

Також ці правила застосовуються при розв’язуванні задач різними способами. Наприклад задачу «На столі лежали 15 маленьких та 7 великих трикутників. Для аплікації використали 5 трикутників. Скільки трикутників залишилось?» можна розв’язати трьома способами:

1 спосіб: 1) 15 + 7 = 22 (тр.)

2) 22 – 5 = 17 (тр.)

2 спосіб: 1) 15 – 5 = 10 (тр.)

2) 10 + 7 = 17 (тр.)

3 спосіб: 1) 7 – 5 = 2 (тр.)

2) 15 + 2 = 17 (тр.).

Читайте також:

1. II. Правила щодо аргументів.
2. V. Етичні правила психологічних досліджень
3. VII. Правила техніки безпеки і гігієни праці.
4. А ви слідуєте цім правилам, коли виступаєте публічно?
5. Види графіків та правила їх побудови.
6. Види графіків та правила їх побудови.
7. Визначення поняття та правила визначення
8. Визначення, класифікація і правила побудови індексів
9. Вимоги до керівника, правила та принцинципи управління
10. Віднімання круглих трицифрових чисел з переходом через розряд виду 420 – 70. Вправи і задачі на застосування вивчених випадків арифметичних дій
11. Віднімання переліків
12. ВІДНІМАННЯ ПОНЯТЬ

Переглядів: 2616