• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Асимптоти графіка функції

Пряма називається асимптотою кривої , якщо відстань від точки 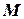кривої до прямої при віддаленні точки 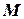у нескінченність прямує до нуля.

Із наведеного означення випливає, що асимптоти можуть існувати лише у тих кривих, які мають як завгодно віддалені точки, тобто у “нескінчених” кривих.

Надалі розрізнятимемо похилі і вертикальні асимптоти. До похилих асимптот належать також і горизонтальні асимптоти.

Теорема.Якщо функція визначена на нескінченості і існують границі

(1)

то пряма є похилою асимптотою кривої при .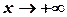

Аналогічно, якщо існують границі

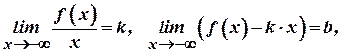(2)

то пряма є похилою асимптотою кривої при .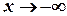

Доведення. Розглянемо випадок 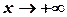. Оскільки за умовою існують границі (1), то . Число 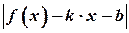дорівнює довжині відрізка від точки прямої до точки графіка функції (рис. 30).

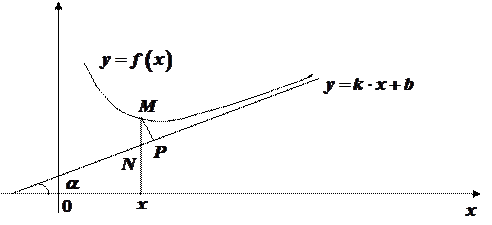
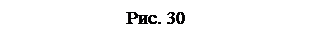
Відстань 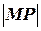від точки до прямої рівна , де 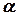- кут, який утворює пряма з додатним напрямом вісі ( 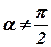, оскільки мова йде про похилі асимптоти). Отже, 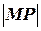=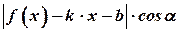. Тоді

.

Випадок, коли 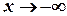доводиться аналогічно.

Якщо , то пряма 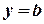є горизонтальною асимптотою графіка функції при 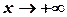. Те ж стосується і випадку .

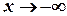Зауваження. Якщо не існує границя 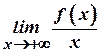, то не існує і границя 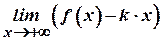. Отже, у цьому випадку графік функції при 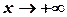асимптот не має. Якщо границя 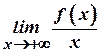існує і рівна 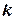, а границя 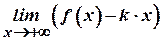не існує, то у цьому випадку графік функції також асимптот не має.

Із означення асимптоти кривої випливає, що пряма є вертикальною асимптотою, якщо принаймні одна з границь або 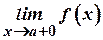рівна 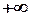або .

3. Загальна схема дослідження функцій і побудови їх графіків

При дослідженні функцій і побудові їх графіків може бути застосована, наприклад, наступна схема:

1. Знайти область визначення функції.

2. Знайти точки розриву та визначити їх тип.

3. Знайти асимптоти графіка функцій.

4. Знайти похідну функції і за її допомогою встановити інтервали зростання і спадання функції.

5. Знайти точки максимуму і мінімуму функції, а також максимальне й мінімальне значення функції.

6. Знайти другу похідну і за її допомогою визначити інтервали опуклості й точки перегину графіка функції.

7. Знайти точки перетину графіка функції з осями координат.

8. Враховуючи одержані результати, побудувати графік функції.

Приклад. Дослідити функцію і побудувати її графік.

Читайте також:

1. Адвокатура в Україні: основні завдання і функції
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Аналіз коефіцієнтів цільової функції
5. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
6. Асимптотична нормальність й ЦПТ
7. Асимптотичний підхід до порівняння оцінок
8. Базальні ядра, їх функції, симптоми ураження
9. Базові функції, логічні функції
10. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
11. Банківська система та її основні функції

Переглядів: 4779