• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Зв’язок між розв’язками прямої та двоїстої задач

Зв’язок між розв’язками прямої та двоїстої задач встановлюється за допомогою двох теорем двоїстості. Для їх доведення використаємо наступну лему.

Лема.

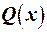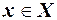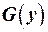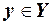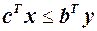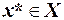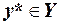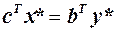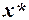Значення функції мети прямої задачі для довільного припустимого розв’язку не перевищує значення функції мети двоїстої задачі для довільного її припустимого розв’язку , тобто . Якщо для деяких та справедлива рівність , то та 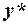— оптимальні розв’язки.

Доведення.

Нехай 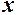та 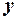— припустимі розв’язки прямої та двоїстої задач, тобто 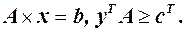Помножимо перший вираз на 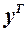зліва, а другий — на 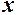справа: 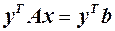, 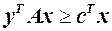. Порівнюючи ці вирази, отримаємо .

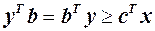Нехай для деяких припустимих 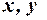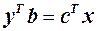. Припустимо, що 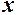— не оптимальний розв’язок. У такому випадку для оптимального розв’язку 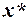справедливе співвідношення 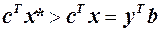, що суперечить вже доведеному вище твердженню. Припустимо, що 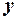— не оптимальний розв’язок. У такому випадку для оптимального розв’язку 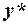справедливе співвідношення 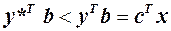, що також суперечить вже доведеному вище твердженню 

1-а теорема двоїстості.

Якщо одна з пари двоїстих задач має розв’язок, то й інша має розв’язок, і оптимальні значення функцій мети рівні між собою — 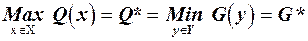. Якщо функція мети для однієї з задач не обмежена , двоїста до неї задача взагалі не має припустимих розв’язків.

Доведення.

Запишемо задачу ЛП в перетвореному вигляді:

,

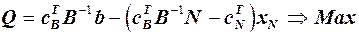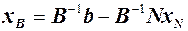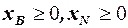, , де .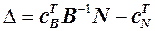

На останній ітерації — в останній симплекс-таблиці розв’язок є оптимальним, 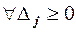, тобто 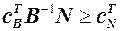. Введемо позначення 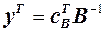. Тоді 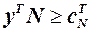, , 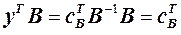і об’єднуючи ці обидва вирази 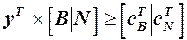, отримаємо .

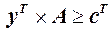Таким чином 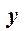— припустимий розв’язок двоїстої задачі. Доведемо, що 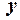— оптимальний розв’язок двоїстої задачі: 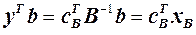. Таким чином значення функції мети для двоїстої задачі для її припустимого розв’язку 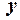дорівнює значенню функції мети прямої задачі для її припустимого розв’язку 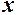. Згідно до леми це означає, що 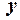є оптимальним розв’язком двоїстої задачі.

Доведемо другу частину теореми.

Нехай відомо, що функція мети прямої задачі не обмежена згори на множині припустимих розв’язків. Припустимо, що двоїста задача при цьому має припустимі розв’язки і 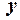— один з них. У такому випадку внаслідок необмеженості функції мети прямої задачі знайдеться такий її розв’язок, для якого 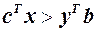, що суперечить лемі 

Примітка.

Твердження, обернене до 2-ї частини теореми 1, взагалі кажучи, є недійсним, тобто, якщо одна з пари двоїстих задач має пусту множину припустимих розв’язків, то інша не обов’язково повинна мати необмежену функцію мети. Обидві задачі можуть бути неприпустимими, наприклад:

Q= 2x₁-x₂ à Max,

x₁- x₂ =1 à y₁

-x₁+x₂ =1 à y₂

x₁ >=0, x₂ >=0 Область припустимих розв’язків .

Умова двоїстої задачі:

G= y₁+ y₂ à Min,

y₁ - y₂ > = 5

2y₁- y₂ > = 2

-y₁+ y₂ > = -1 Область припустимих розв’язків .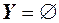

Теорема 2.

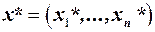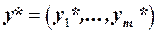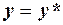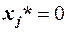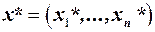Нехай , — припустимі розв’язки прямої та двоїстої задач відповідно. Якщо для кожного j, для якого відповідне j-те обмеження двоїстої задачі перетворюється при в строгу нерівність, , то та 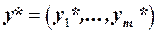є оптимальними розв’язками прямої та двоїстої задач.

Ця теорема може бути також сформульована у наступному еквівалентному вигляді. Розв’язки 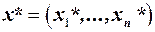, 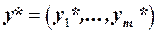є оптимальними тоді і лише тоді, якщо виконуються співвідношення:

,

.

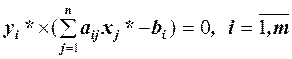Ця теорема дає можливість за оптимальним розв’язком однієї з задач знайти оптимальний розв’язок двоїстої до неї.

Доведення.

Нехай для кожного 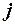, для якого 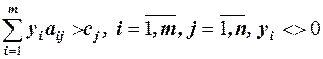, маємо 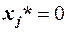. Тоді 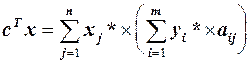. Справді, ті складові, для яких 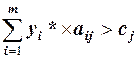, фактично рівні нулю, оскільки для них 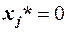. Залишаються до розгляду лише ті складові, для яких 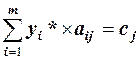, що доводить справедливість рівності. Після перегрупування суми отримаємо 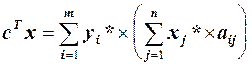. Оскільки 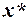- припустимий розв’язок прямої задачі, то суми в дужках рівні відповідним значенням 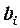, тобто 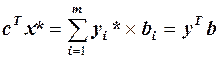і згідно до леми ці розв’язки є оптимальними.

A. Нехай тепер навпаки, відомо, що 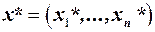, 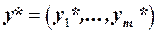— оптимальні розв’язки прямої та двоїстої задач. Тоді за першою теоремою двоїстості 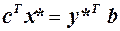. Оскільки 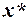— припустимий розв’язок задачі, то 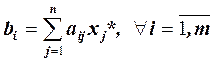. Підставляючи ці вирази в рівність та перегруповуючи складові в лівій частині, отримаємо: 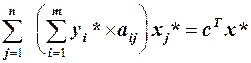. Якщо хоча б для одного j, для якого 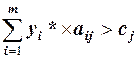, було б 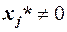, то попереднє співвідношення не виконувалося б. Тобто дійсно, для кожного j, для якого б виконувалося попередня строга нерівність, отримуємо 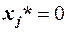, що й потрібно було довести 

Переглядів: 1364