Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Парна регресія

Зв’язок між показником 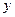та фактором 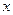з урахуванням можливих відхилень запишемо у вигляді:

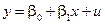
де 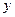–результативна змінна; 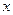– факторна змінна; 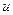– стохастична складова, яка вводиться до моделі з метою урахувати наявність впливу факторів, які не входять до моделі, 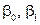– параметри моделі.

Залежність:

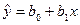
де 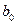та – оцінки параметрів моделі, яка характеризує середнє значення показника для кожного значення фактора, називається регресією.

Щоб оцінити параметри моделі необхідно сформувати сукупність спостережень, кожна одиниця якої характеризуватиметься значеннями змінних 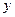та 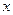. Множину точок на координатній площині, які відповідають парам значень показника та фактора, називають кореляційним полем точок.

На підставі гіпотези про лінійність зв’язку між показником та фактором, через кореляційне поле точок можна провести безліч прямих, які різняться між собою параметрами 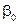та 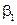. Те, що відхилення фактичних значень від розрахункових матимуть переважно знак «-» чи «+» , підтверджує, що вони мають невипадковий характер, тобто пряма лінія неадекватно описує залежність.

Справжні значення параметрів обчислити не можливо, оскільки ми маємо обмежене число спостережень, тому знайдені розрахункові значення параметрів 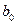та є статистичними оцінками справжніх параметрів 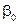і .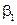

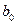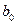Принцип найменших квадратів відхилень полягає в знаходженні таких оцінок та , для яких сума квадратів відхилень теоретичних значень показника від фактичних найменша. Необхідна умова для цього – рівні нулю частинні похідні цієї функції за кожною з оцінок параметрів та .

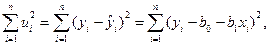
Тоді

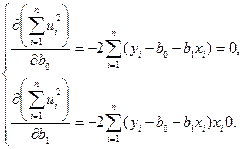
Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь:

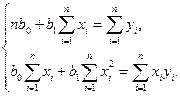
Розв’язавши цю систему, ми отримаємо формули, на основі яких можна обчислити значення оцінок параметрів 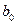та :

, .

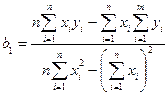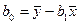Остання формула випливає не з системи рівнянь, а з суті методу найменших квадратів. Оцінки найменших квадратів такі, що лінія регресії обов’язково проходить через точку 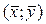. Підставивши середні значення змінних в рівняння регресії, ми знайдемо оцінку параметра .

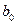Кількість ступенів вільності показує, скільки незалежних елементів інформації, що утворились з елементів 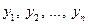, потрібно для розрахунку даної суми квадратів.

В статистиці кількістю ступенів вільності певної величини часто називають різницю між кількістю різних дослідів і кількістю констант, знайдених завдяки цим дослідам незалежно один від одного. Окреме застосування цього поняття відноситься до суми квадратів.

Розглянемо, скільки ступенів вільності має кожна визначена сума квадратів.

Почнемо із загальної суми квадратів. Для її утворення потрібно 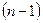незалежних чисел, тому що з чисел 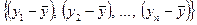незалежні тільки 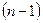завдяки властивості:

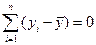
Суму квадратів, що пояснює регресію, отримують, використовуючи тільки одну незалежну одиницю інформації, яка утворюється з 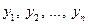, а саме .

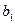Покажемо, що, справді, нахил 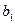можна подати як функцію від .

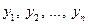Запишемо відхилення, що пояснює регресію у вигляді: 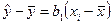. Маємо:

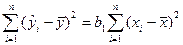
Отже, суму квадратів, що пояснює просту лінійну регресію, можна утворити, використовуючи тільки ну одиницю незалежної інформації, а саме 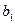(для випадку багатофакторної регресії маємо іншу ситуацію, яку розглянемо пізніше). Звідси розглядувана сума квадратів має один ступінь вільності. Потрібно звернути увагу на те, що ступінь вільності в даному разі збігається з кількістю залежних змінних, що входять у регресійну модель. Сума квадратів помилок має 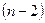ступенів вільності. Ця сума базується на кількості ступенів вільності, яка дорівнює різниці між кількістю спостережень і кількістю параметрів, що оцінюються. У разі простої лінійної регресії оцінюються два параметри 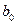та 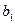. Якщо позначити кількість спостережень через 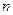, то для цієї суми квадратів маємо 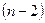ступенів вільності.

У разі простої лінійної регресії ступені вільності, як і суми квадратів, можна розкласти таким чином: .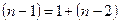

Параметри регресії у невеликих за обсягом сукупностях здатні до випадкових коливань. Тому здійснюють перевірку їх істотності або статистичної значимості за допомогою 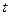–критерію Ст’юдента.

Можна показати, що параметри, знайдені за МНК, розподілені за нормальним законом розподілу, що формалізовано можна записати таким чином:

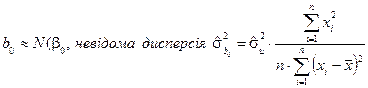
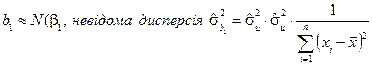
В загальному випадку дисперсії оцінок параметрів 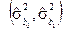невідомі, тому що не можна обчислити 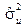, бо випадкові величини взагалі є не спостережуваними. Але ми можемо обчислити оцінку дисперсій 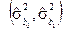, тобто знайти:

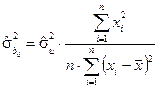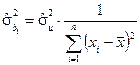
де 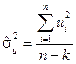, 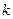– кількість оцінених параметрів.

А потім побудувати 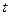–статистику для кожного параметра:

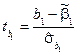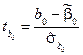
з 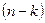ступенями вільності, де 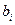– оцінка параметра 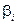, отримана за МНК; 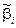– гіпотетичне значення, яке має набути параметр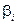 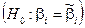; 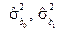оцінки дисперсій параметрів відповідно.

В економетрії поширеною формою нуль-гіпотези є така: 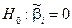проти альтернативної .

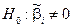В цьому разі 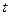–статистика для параметрів має вигляд:

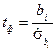
Критичне значення критерію Ст’юдента 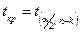для рівня значимості 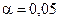(задається дослідником) та 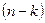ступенів вільності ( 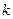– кількість параметрів ) знаходимо за допомогою таблиць 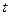–розподілу Ст’юдента. Якщо < 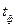, то оцінка 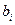вважається статистично значимою.

Для того щоб визначити, як параметри 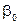та 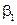пов’язані з їх оцінками 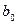та 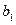, потрібно побудувати інтервали довіри для параметрів узагальненої регресійної моделі, тобто такі інтервали, в які з заданою ймовірністю потрапляють їхні значення.

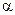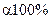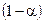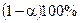Процедура побудови інтервалів довіри є аналогічною процедурі тестування значимості знайдених параметрів простої вибіркової лінійної регресії. Спочатку обираємо рівень значимості ( або ), відповідно рівень довіри буде дорівнювати або . За 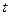- таблицею Ст’юдента знаходимо значення 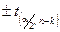з 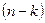ступенями вільності. Тоді можемо записати:

– довірчі межі коефіцієнта регресії : 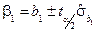зі ймовірністю ;

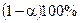– довірчі межі вільного члена: 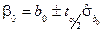зі ймовірністю .

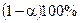Поряд з визначенням характеру зв’язку важливе значення має оцінка щільності зв’язку, тобто оцінка узгодженості варіації взаємозв’язаних показників. Якщо вплив факторного показника на результативний значний, то це виявиться в закономірній зміні значень результативного показника зі зміною значень факторного, тобто фактор 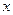своїм впливом формує варіацію 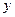. За відсутності зв’язку варіація 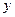не залежить від варіації .

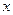Для оцінювання щільності зв’язку використовують низку коефіцієнтів з такими спільними властивостями:

1. За відсутності будь-якого зв’язку значення коефіцієнта наближається до нуля; при функціональному зв’язку – до одиниці.

2. За наявності кореляційного зв’язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв’язок.

Серед мір щільності зв’язку найпоширенішим є коефіцієнт кореляції Пірсона. Сфера його використання обмежується лінійною залежністю. Обчислення лінійного коефіцієнта кореляції ґрунтується на аналізі відхилень значень взаємозв’язаних ознак 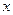та 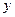від середніх.

За наявності прямого кореляційного зв’язку будь-якому значенню 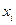> 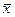відповідає значення 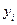> 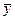, а 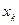< 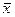відповідає < .

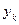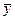Коефіцієнт кореляції визначається відношенням зазначених сум:

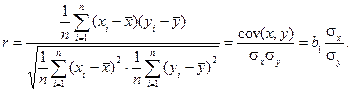
В разі функціонального зв’язку фактична сума відхилень дорівнює граничній, а коефіцієнт кореляції 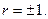При кореляційному зв’язку абсолютне його значення буде тим більшим, чим щільніший зв’язок. Якщо значення лінійного коефіцієнта кореляції близьке до 1 і 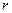>0 , то можна зробити висновок про досить тісний прямий зв’язок між 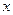та 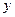. І навпаки. Якщо 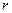<0, то зв’язок між ознаками зворотній.

Вимірювання щільності нелінійного зв’язку ґрунтується на співвідношенні варіацій теоретичних та емпіричних значень результативної ознаки. Відхилення індивідуального значення ознаки 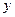від середньої 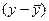можна розкласти на дві складові. У регресійному аналізі це відхилення від лінії регресії 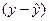та відхилення лінії регресії від середньої .

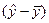Відхилення 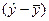є наслідком дії фактора 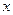, відхилення 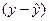– наслідком дії інших факторів. Взаємозв’язок факторної та залишкової варіації описується правилом декомпозиції варіацій: загальну дисперсію результативної ознаки можна розкласти на дві частини - дисперсію, що пояснює регресію, та дисперсію помилок:

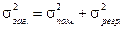
де 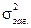– загальна дисперсія; 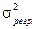– факторна дисперсія; 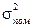– залишкова дисперсія, або дисперсія помилок.

Очевидно, значення факторної дисперсії буде тим більшим, чим сильніший вплив фактор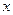а та .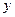

Поділивши обидві частини на загальну дисперсію, отримаємо:

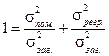
Перша частина цього виразу являє собою частину дисперсії, яку не можна пояснити через регресійний зв’язок, друга - частину дисперсії, яку можна пояснити, виходячи з регресії. Вона називається коефіцієнтом детермінації і використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної:

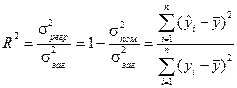
Для лінійного зв’язку: .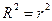

Якщо значення коефіцієнта детермінації близьке до одиниці, то можна вважати, що побудована модель адекватна ( 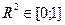). Варіація 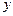на 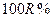залежить від варіації 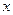, і на 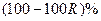від варіації інших факторів, які не враховуються в моделі.

При аналізі лінійної моделі на адекватність необхідно детально проаналізувати похибку спостереження:

– якщо похибка двічі змінює свій знак, то лінійна модель не адекватна;

– якщо похибка від виміру до виміру систематично зростає або спадає, то лінійна модель також є не адекватною.

Адекватність простої лінійної регресійної моделі можна перевірити за допомогою коефіцієнта детермінації. Якщо його значення близьке до одиниці, то можна вважати, що модель адекватна. Якщо його значення близьке до нуля, то модель неадекватна, тобто немає лінійного зв’язку залежною та незалежною змінними. Але який висновок можна зробити, якщо значення коефіцієнта кореляції має не явно виражене граничне значення, наприклад, 0,5; 0,45; 0,44 і т.ін.? Зрозуміло, що в таких випадках важко зробити однозначний висновок про наявність зв’язку, тобто про адекватність моделі. Нам потрібен інший критерій, який би однозначно давав відповідь на запитання про адекватність побудованої моделі. Найбільш поширеним із таких критеріїв є критерій Фішера.

Перевірка моделі на адекватність за 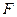–критерієм Фішера складається з таких етапів:

1. Розраховуємо величину 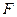–критерію:

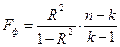
В цій формулі 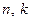– кількість спостережень та кількість параметрів відповідно.

2. Задаємо рівень значимості, наприклад, 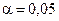. Тобто, ми вважатимемо, що можлива помилка для нас становить 0,05, це означає, що ми можемо помилитися не більш, ніж у 5% випадків, а в 95% випадків наші висновки будуть правильними.

3. На цьому етапі за статистичними таблицями 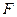–розподілу Фішера з 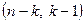ступенями вільності та рівнем значимості 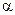знаходимо критичне значення 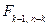. Якщо 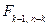< 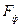, то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною. Або навпаки, якщо > .

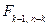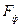Якщо побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної. Прогнози ми можемо отримати двох видів: точковий – дає значення змінної 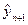для відповідного значення 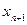з побудованої вибіркової моделі: 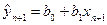; інтервальний .

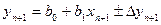При цьому, виходячи з узагальненої моделі, дійсне значення для прогнозного періоду буде дорівнювати: .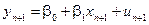

Дійсне значення результату ми знайти не можемо, а можемо лише оцінити його за допомогою прогнозу.

Отже, прогнозне значення 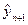є оцінкою дійсного значення змінної 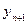. Таким чином з нашої вибіркової моделі ми легко можемо знаходити будь-яке прогнозне значення.

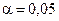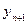Виходячи з отриманого точкового прогнозу можна побудувати інтервали довіри для його дійсного значення. Такий інтервал довіри при заданому рівні значимості для знаходять за формулою:

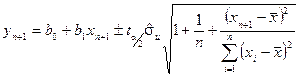
При цьому 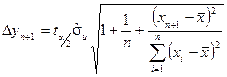– похибка прогнозу.

На практиці більш важлива побудова інтервалів довіри для математичного сподівання 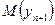, тобто побудова інтервалів довіри для .

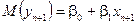В цьому випадку формула модифікується:

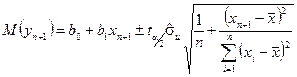
<== попередня сторінка	\|	наступна сторінка ==>
Умови практичних завдань контрольної роботи	\|	Багатофакторна регресія

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.