Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Система Рабіна

RSA

2.1. Опис системи. Запропонована 1977 року система RSA є чи не найпопулярнішою криптосистемою з відкритим ключем. Назва системи утворена зперших літер імен її винахідників — Рональда Райвеста, Аді Шаміра та Леопарда Адлемана.

Генерування ключів. Вибирають два досить великі прості числа р і q. Для їх добутку п = pq значення функції Ойлера дорівнює ф(п) = (р - 1)(q - 1) = п – р – q + 1. Далі випадковим чином вибирають елемент е, щоне перевищує значення ф(п) і взаємно простий з ним. Іншими словами, е є випадковим елементом із множини 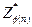. Для е за алгоритмом Евкліда знаходить елемент d, обернений до е в 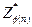, тобто такий, що d < ф(п) і

(1)

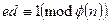
Як результат покладають:

Відкритий ключ: е, п.

Таємний ключ: d.

Шифрування відбувається блоками. Для цього повідомлення записують у цифровій формі і розбивають на блоки так, що кожен блок позначає число, яке не перевищує п. Скажімо, якщо блок записаний у вигляді двійкового слова довжини m, то повинна виконуватись нерівність 2^m < n. Блок М розглядається як елемент кільця Z_n і як такий, може підноситись до степеня за модулем п.

Алгоритм шифрування Е у системі RSA полягає у піднесенні М до степеня е. Записуємо це так:

Е(М) = M^e mod п.

ніякого ефективного алгоритму. Однак не доведено, що такого алгоритму не існує. На жаль, така ситуація є типовою для всіх криптосистем з відкритим ключем, що мають практичний інтерес. Єдине, що ми можемо зробити, і що є нашим завданням у цьому пункті, це розглянути деякі специфічні методи криптоаналізу для RSA і оцінити їхню (без)перспективність.

Будь-яку асиметричну криптосистему можна зламати, вказавши ефективний спосіб визначення таємного ключа за відкритим. У нашому випадку це означає, що розкриття RSA зводиться до задачі

знаходження таємного ключа для RSA

Задано: е, п, де п = pq і НСД (е, ф(п)) = 1.

Знайти: d таке, що x^ed = х (mod п) для всіх х.

З алгоритму генерування ключів безпосередньо випливає, що остання задача зводиться до обчислення значення функції Ойлера ф(п). Як нам відомо з пункту IV.5.1, обчислення функції Ойлера від аргументів такого типу є задачею еквівалентною до знаходження співмножників р і q числа п. Отже, спроба факторизувати модуль п = pq є найочевиднішим шляхом до розкриття RSA. На щастя, як зазначалось в § IV.З, на сьогодні це є безнадійною справою для п порядку 10²⁰⁰. Тому при генеруванні ключа, р і q рекомендується вибирати із приблизно сотнею десяткових цифр кожне. Вибір таких чисел повинен бути справді випадковим, щоб уникнути можливої факторизації якимось із вузькоспеціальних методів (див. обговорення в пункті IV.2.7 і § IV.З разом із задачами). Звідси також високі вимоги до якості генератора псевдовипадкових бітів, що використовується алгоритмом породження простих чисел.

Природно виникає питання, чи не можна розв'язати задачу визначення таємного ключа, обходячись без факторизації. За твердженням 2.3, цю задачу можна переформулювати як задачу знаходження такого d, що ed - 1 ділиться на ф(п). Але для такого d число т = ed - 1 можна використати для розкладу п на множники за допомогою ймовірнісної процедури, описаної в пункті IV.5.2. Отже, визначення таємного ключа для RSA є таким же важким, як факторизація модуля п. Підсумовуючи наші аргументи, отримуємо

твердження 2.4. Знаходження таємного ключа для RSA е еквівалентним до факторизації чисел, що є добутком двох простих, відносно поліноміальної ймовірнісної звідності.

Зауважимо, що для деяких повідомлень М має місце рівність Е(М) = М. Числові еквіваленти таких повідомлень є розв'язками конгруенції 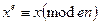в Z_n, кількість яких нескладно порахувати (див. вправу 2.5).

Виявляється, що доля повідомлень, які подібно до наведеного прикладу можуть бути розкриті якимось простим специфічним способом, не може бути великою, хіба що всі повідомлення можуть бути дешифровані подібним чином.

Щоб формалізувати цей факт, введемо такі позначення. Припустимо, що для кожної пари е і п таких, що НСД(е,φ(п)) = 1, маємо деяку підмножину У_e_,_n кільця Z_n. Через δ_n = min_e||У_e_,_n||/п позначимо мінімальну по е щільність У_е,п в Z_n. Звуженням задачі розкриття RSA на родину підмножин У_e_,_n назвемо таку задачу.

Задано: е, п, у, де п = pq, НСД (е, ф(п)) і у У_е_,_n Знайти: х таке, що х^е y(mod n).

твердження 2.5. Для довільної родини підмножин 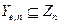задача розкриття RSA ймовірнісна зводиться до свого звуження на Y_e_,_n за час, обмежений деяким поліномом від довжини входу і величини 1/δ_п.

Таким чином, якщо не існує ймовірнісного поліноміального алгоритму для розкриття RSA, то нема й такого алгоритму, який би розкривав частку 1/log^cп всіх можливих криптотекстів, де с — константа. Іншими словами, будь-який спосіб розкриття лише частки l/log^c n всіх можливих криптотекстів можна використати для розкриття абсолютно всіх криптотекстів.

доведення. Припустимо, що в нас є оракул, який, отримавши запит (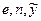), видає деякий елемент 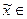Z_n із властивістю 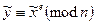, справедливою завжди, коли 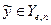Тоді RSA ламається таким ймовірнісним алгоритмом.

Вхід: е, п, у, де п = pq і НСД (е, ф(п)) = 1.

• Обчислити НСД (y, п). Якщо 1 < НСД (у, п) < п, то знайдено нетривіальний дільник модуля п, і криптосистема ламається визначенням таємного ключа d. Якщо НСД (у, п) = п, то подати на вихід х = 0. Якщо НСД (у, п) = 1, то продовжувати.

• Вибрати випадковий елемент 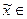Z_n. Якщо НСД 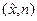> 1, то теж отримано нетривіальний дільник модуля п. Якщо

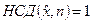(1)

то продовжувати.

• Обчислити

(2)

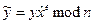• Зробити оракулові запит .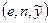

• Отримавши відповідь , перевірити чи справді

(3)

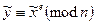Якщо ні, визнати невдачу; інакше продовжувати.

• Обчислити і подати на вихід

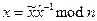, (4)

де 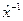— елемент, обернений до в .

Позначимо ймовірність невдачі описаного алгоритму через αіоцінимо її. У виродженому випадку, коли НСД (у, п) > 1, маємо α = 0. Проаналізуємо роботу алгоритму на входах, для яких НСД (у, п) = 1.

Алгоритм зразу досягає успіху в тому щасливому випадку, коли НСД 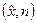> 1. Це трапляється з імовірністю 1 - ф(п)/п = l/p+ 1/q -1/п, тому першою нашою оцінкою є

(5)

Розглянемо випадок, коли має місце (1). Основою нашого аналізу є спостереження, що коли 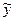попадає в У_e_,_n, то алгоритм справді видає відкритий текст х, що відповідає криптотекстові у, тобто виконується умова 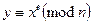. Справді, ця конгруенція випливає безпосередньо із співвідношень (2), (3) і (4).

Таким чином, алгоритм зазнає невдачі лише у випадку, коли 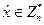і Ймовірність першої з цих двох подій дорівнює ф(п}/п. Оцінимо ймовірність другої події, припустивши, що перша має місце. Зробимо також припущення, що

δ_п>1-ф(п)/п. (6)

Тоді для кожного е. щільність множини в не менша, ніж δ_п-(1-ф(n)/п). Щонайменше з такою ймовірністю 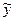потрапляє в У_е_,_n, бо за умови (1) 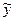є випадковим елементом множини . Підсумовуючи, отримуємо оцінку

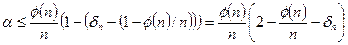
Використовуючи нерівність 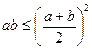, отримаємо звідси оцінку

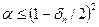. (7)

Нагадаємо, що ми довели (7) на основі припущення (6). Якщо ж (6) не виконується, тобто ф(п)/п ≤ 1 – δ_n, то за (5) маємо нерівність α ≤ 1 – δ_n, звідки випливає та ж оцінка (7).

Щоб зменшити ймовірність невдачі, описаний алгоритм слід виконати k разів, як описано у пункті III. 3.1. Для k = [t/δ_n] ймовірність невдачі буде меншою, ніж

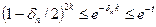
ВПРАВИ

2.1. а) Сформувати відкритий і таємний ключі для системи RSA на основі р = 47, q = 71, е = 19.

b) Зашифрувати повідомлення КУПИ. При переході до цифрової форми замінювати кожну літеру її двоцифровим десятковим номером в алфавіті. Цифрове повідомлення розбивати на блоки по 4 цифри.

c) Дешифрувати криптотекст 3011 1211.

2.2.Підрахувати кількість повідомлень , для яких НСД (М, п) > 1. (Пересилання таких повідомлень слід виключити, бо з їх перехопленням суперник отримує нетривіальний дільник модуля п.)

2.3.Зламати RSA у випадку, коли

a) р і q — прості числа-близнята;

b) різниця q — р невелика.

2.4. Аліса, Боб і Бернар є абонентами комунікаційної мережі. Для захисту інформації в мережі використовується система RSA, причому ключі генеруються і розподіляються між абонентами менеджером мережі.

a) ([142]) Боб і Бернар користуються відкритими ключами (е₁,п) та (е₂,п), де е₁ та e₂ взаємно прості. Аліса послала кожному з них одне і те ж повідомлення М. Пояснити, як можна визначити М за криптотекстами С₁ = М^e¹ mod п та С₂ = М^e² mod n.

b) ([85]) Пояснити, як Боб може визначити Бернарів таємний ключ d₂, a Бернар — Бобів ключ d₁.

Обговорення подібної проблематики див. в [47].

2.5. а) Для п = рd, добутку двох різних простих, порахувати кількість елементів 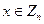, які задовольняють конгруенцію .

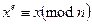b) Знайти всі розв'язки конгруенції в Z₁₅.

2.6. Суперник перехопив криптотекст 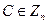, зашифрований з допомогою відкритого ключа (е,п), і один за другим обчислює члени послідовності С² mod п, С³ mod п,.... Довести, що зробивши не більш як ψ(п) кроків, суперник гарантовано отримає відкритий текст. (Інша причина слідкувати, щоб ψ(п) було великим чи, еквівалентно, НСД (р - 1, q - 1) малим, відображена у вправі IV.3.2.)

2.7. Довести, що ф(ψ(п)) - 1 ітерацій досить, щоб розкрити систему RSA методом ітерацій.

ЛІТЕРАТУРА

Оригінальною публікацією про систему RSA є [132]. Популярний виклад можна знайти в [16].

З метою пришвидшення процедури шифрування пропонувалось завжди використовувати експоненту е = 3 замість того, щоб щоразу вибирати її випадковим чином. Проте у [103] показано, що використання невеликого параметра е дає можливість супернику розкрити повідомлення у випадку, якщо воно розіслане кільком користувачам криптосистеми.

Твердження 2.5 наведене у [131] із посиланням на Яо. Воно показує, що система RSA однаково надійна (чи ненадійна) як для всіх повідомлень, так і для будь-якої малої їх частини. Таку однорідність теж можна вважати свідченням на користь надійності RSA. Інші властивості такого ж плану доведено в [101, 67, 73] (див. також вправу VI.1.4).

ЛЕКЦІЯ 17

Цю криптосистему запропоновано в [130].

Генерування ключів. Вибирають два великі прості числа р і q. Обчислюють їх добуток п = pq. Покладають

Відкритий ключ: п.

Таємний ключ: р, q.

Шифрування відбувається блоками подібно до системи RSA, згідно з формулою

Е(М) = М² mod п.

Дешифрування. Якщо Е(М) = С,то М є квадратним коренем числа С за модулем п. За умови НСД (С, п) = 1, в Z_n таких коренів є рівно чотири (пункт 3 твердження IV. 4.1). Результати пунктів IV. 4. 3 і IV. 4. 2 дають ефективний алгоритм добування всіх квадратних коренів за модулем п, який використовує співмножники р і q (тобто таємний ключ!). Саме цей алгоритм використовується в системі Рабіна при дешифруванні. Після знаходження всіх чотирьох коренів з них вибирається той, який є числовим еквівалентом осмисленого тексту.

Зауваження 3.1. В системі Рабіна шифруюче відображення не є ін'єктивним, але може бути зробленим таким шляхом простої модифікації. Однозначності можна досягти за рахунок передачі разом із криптотекстом деякої додаткової незашифрованої інформації (вправа 3.2). Це справді необхідно, коли шифрується не текстова, а суто числова інформація.

Зауваження 3.2. При описі алгоритму шифрування ми виходили з припущення, що НСД (С, п) = 1 (це еквівалентно з НСД (М, п) = 1). Посилання повідомлень С, для яких НСД (С, п) > 1, слід виключити, бо з їх перехопленням суперник отримує нетривіальний дільник НСД (С, п) числа п, тобто дізнається таємний ключ.

Приклад 3.3. Нехай таємний ключ вибрано так: р = 53 і q = 67. Тоді відкритим ключем буде п = 3551.

Розглянемо шифрування повідомлення ПРОДАЙ. Як це було зроблено у прикладі 2.1, спочатку повідомлення записується у цифровій формі і розбивається на блоки по чотири цифри: 1920 1805 0013. Перший блок 1920 перетворюється у 1920² mod 3551 = 0462. Подібно шифруються наступні два блоки, і в результаті виходить криптотекст 0462 1758 0169.

Припустимо тепер, що ми отримали криптотекст 1497. Для дешифрування слід з нього добути квадратні корені за модулем 3551. З цією метою добуваємо корені за простими модулями 53 і 67 із лишків 1497 mod 53 = 13 і 1497 mod 67 = 23, відповідно. Застосовуємо алгоритм із пункту IV.4.2. Модуль 53 належить до випадку 2, а 67 до випадку 1. Знаходимо 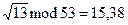, і . За допомогою алгоритму з Китайської теореми про остачі визначаємо чотири корені з 1497 за модулем 3551:(15,31) = 0969, (15,36) = 1711, (38,31) = 1840, (38,36) = 2582. Як зразу видно, лише другий корінь є числовим еквівалентом тексту в українській абетці, а саме повідомлення НІ.

Ефективність. Процедура вибору великих простих р і q описана в пункті IV.2.7. Зауважимо, що при алгоритм дешифрування буде особливо простим (випадок 1 алгоритму з пункту IV.4.2).

Надійність. Зрозуміло, що задача розкриття системи Рабіна, тобто знаходження за С такого М, що Е(М) = С, є нічим іншим, як задачею добування квадратного кореня за модулем п = pq. В пункті IV.4.3 показано, що остання є такою ж складною, як задача факторизації числа п = pq (яка, до речі, у нашому випадку є задачею знаходження таємного ключа за відкритим). Див. також вправу 3.4.

ВПРАВИ

3.1. Нехай р = 59 і q = 67. :

a) Зашифрувати повідомлення ДЕСЯТЬ.

b) Розшифрувати криптотекст 0753 2556.

3.2.Нехай х — квадратичний лишок за модулем п = pq, де п є цілим Блюма, тобто ріq — різні прості з властивістю . Довести, що кожен із чотирьох квадратних коренів з х в Z_n однозначно визначається парою бітів b₁, b₂, які для 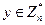рівні

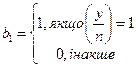
3.3.Довести, що відображення Е(х) = х² mod п, для п = pq — цілого
Блюма, є бієкціею з Q_n на Q_n.

3.4.Показати, що система Рабіна нестійка до атаки з вибраним криптотектом.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Концепція	\|	Ймовірнісне криптування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.