
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 4. Числові та блочні матриці
4.1 Поняття матриці та вектору
См. рукопись МОТС с.1
4.2 Мінор та алгебраїчне доповнення
См. рукопись МОТС с.1
4.3 Визначник матриці
См. рукопись МОТС с.1, 2
4.4 Сума та добуток матриць
Сумою двох прямокутних матриць A та B однакових розмврів m×n називають матрицю С такогож розміру, кожен елемент якої дорівнює сумі відповідних елементів матриць складових. Суму позначають як
 , (4.1)
, (4.1)
де
 .
.
Приклад.
 . (4.2)
. (4.2)
Добутком матриці А на скаляр αназивають матрицю С розміру m×n, що співпадає з розміром матриці А, елементи якої отримують множенням кожного елементу матриці А на скаляр α:
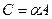 , (4.3)
, (4.3)
якщо
 .
.
Приклад.
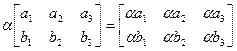 . (4.4)
. (4.4)
Легко бачити, що
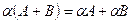 ;
; 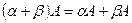 ;
;  . (4.5)
. (4.5)
Добутком двох прямокутних матриць A розміру m×n та B розміру n×q називають матрицю C розміру m×q, у якої елемент cij , що стоїть на перетині строки з номером і та стовбчика з номером j, дорівнює сумі добутків елементів строки номер і матриці A та стовбчика номер j матриці B:
 (4.6)
(4.6)
та позначають
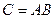 .
.
Приклад.
 . (4.7)
. (4.7)
Множення матриць є непереставною операцією. Іншою мовою
 .
.
Добуток матиць має декілька властивостей
 ;
;  ;
;  .
.
4.5 Блочні матриці. Визначник блочної матриці
Будь-яку матрицю з допомогою вертикальних та горизонтальних ліній можна розділити на блоки. Таке розділення в деяких випадках суттєво спарощує знаходження добутку матриць та її визначника.
Якщо матриця F розділена на чотири блоки
 , (4.8)
, (4.8)
то визначник цієї матриці може бути знайдено за формулою
 . (4.9)
. (4.9)
Приклад.
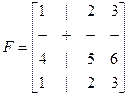 .
.
 ;
; 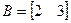 ;
; 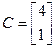 ;
; 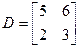 .
.

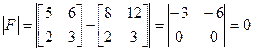 .
.
Тема 5. Обертання матриці та її характеристики
5.1 Алгоритми обертання матриці
Зворотною по відношенню до матриці А розміру n×n називають таку матрицю А-1 , що визначається з рівняння
 , (4.10)
, (4.10)
де |A| - визначник матриці А; Апр – приєднана до А матриця (асоційована з А матриця). В свою чергу приєднана матриця Апр є [Ланкастер] транспонованою матрицею алгебраичних доповнень до елементів матриці А
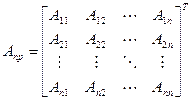 . (4.11)
. (4.11)
Таким чином, для обертання матриці необхідно спочатку знайти визначник |A| та впевнитись у тому, що вихідна матриця не є особливою, а потім скласти приєднану матрицю.
Приклад.
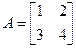 .
.
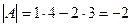 .
.
Оскільки |A| не дорівнює нулю, то вихідна матриця не є особливою, тому иснує обернена. Знайдемо матрицю алгебраичних доповнень до елементів матриці А
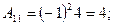


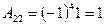 .
.
Враховуючи отриманий результат можна записати
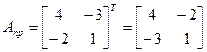 .
.
Таким чином,
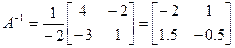 .
.
Визначена як показано вище обернена матриця має наступну головну властивість
 . (4.12)
. (4.12)
Для обернення добутку матриць А, В можна скористатися формулою
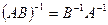 . (4.13)
. (4.13)
5.2 Власне значення матриці
Власним значенням матриці А розміру n×n (власним числом, характеристичним числом) називають таке значення аргументу λ, при якому матриця

є особливою. В наведеній формулі En – одинична матриця розміру n×n. Кількість власних значень матриці дорівнює її розміру. Множина усіх власних значень матриці утворює її спектр.
Звідси для того, щоб визначити спектр матриці необхідно знайти корені одного з наступних алгебраічних рівнянь
 ;
;  . (4.14)
. (4.14)
Рівнянння (4.14) називають характеристичне або вікове рівняння матриці.
Приклад.
Задана матриця 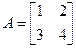 . Необхідно знайти її власні значення.
. Необхідно знайти її власні значення.
Визначимо характеристичне рівняння
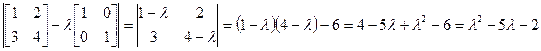 ,
,
отже характеристичне рівняння має наступний вигляд
 .
.
Звідси
 ;
;  ;
;  .
.
5.3 Власний вектор матриці
5.4 Проектори матриці
5.5 Жорданова форма матриці
5.6 Матрична експонента
Матричною експонентою для числової матриці А називають функцію еAt , яка дорівнює сумі наступного ряду
 (4.15)
(4.15)
де t незалежна змінна. Частіше за все – це час.
Знаходження суми (4.15) можна здійснити декількома способами.
5.6.1. На основі зворотного передтворення Лаласа
Якщо матриця A має розмір n×n, то на основі пететворення Лапласа функції еAt можна записати, що
 ,
,
де s -
Таким чином, для знаходження матричної експоненти можливо виконати наступні дії:
1. Знайти матрицю F1 у вигляді
 . (4.16)
. (4.16)
2. Обернути матрицю F1 та визначити зображення лапласа матричної експоненти F0(s)
 . (4.17)
. (4.17)
3. Знайти зворотне перетворення Лапласа та визначити матричну експоненту
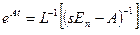 . (4.18)
. (4.18)
Приклад
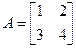 ;
;  ;
; 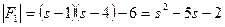 ;
;
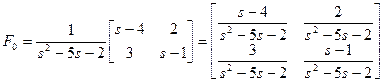
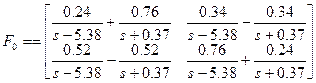 ;
;  .
.
5.6.2. Знаходження матричної експоненти методом діагоналізації
Якщо матриця A розміру n×n є неособливою та діагональною, то матрична експонента для такої матриці є діагональною матрицею такого ж розміру та дорівнює
 , (4.19)
, (4.19)
де λі – власні числа матриці А. Якщо вихідна матриця А не є діагональною, то її необхідно привести до такого вигляду в результаті знаходження наступного добутку
 , (4.20)
, (4.20)
де Т – є матрицею розміру n×n, стовбичики якої є власними векторами матриці А.
В такому разі, матрична експонента дорівнює
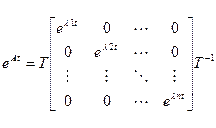 . (4.21)
. (4.21)
Таким чином алгоритм пошуку матричної експоненти даним методом полягає у наступному.
1. Знайти власні числа матриці А.
2. Знайти власні вектори матриці А.
3. Сформувати діагональну матрицю  .
.
4. Сформувати діагональну матрицю Т.
5. Обернути Т.
6. Розрахувати матричну експоненту.
Приклад.
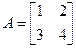 .
. 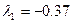 ;
; 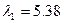 ;
; 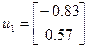 ;
;  ;
;  ;
;
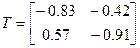 ;
;  ;
;
 ;
;
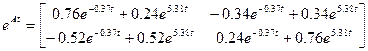 .
.
Читайте також:
- IV. На четвертому етапі, виходячи із позиції кожної СОБ на матриці АДЛ, вибирають для неї відповідну стратегію.
- Визначення складових для побудови матриці SPACE-аналізу
- Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
- Вимоги, що пред'являються до волокон і матриці
- Власні числа та власні вектори матриці
- Власні числа та власні вектори матриці
- Властивості матриці інцидентності
- Властивості оберненої матриці.
- Елементарні перетворення матриці.
- Елементарні перетворення рядків матриці
- Етапи побудови матриці Бостонської консультативної групи.
- Етапи побудови матриці Бостонської консультативної групи.
| <== попередня сторінка | | | наступна сторінка ==> |
| | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |