• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівнопотужні множини

В теорії множин існує поняття рівнопотужних множин. Уточнимо дане поняття.

Означення.Множини Х і Y називаються рівнопотужними, якщо вони або порожні, або між ними встановлено взаємно однозначну відповідність.

Позначається рівнопотужність множин: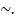

Якщо множина Х рівнопотужна множині Y, то записують так: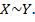

Рівнопотужність множин має свої характерні властивості:

1) Рефлективність: 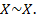Будь яка множина рівнопотужна сама собі.

2) Симетричність:

3) Транзитивність: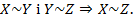

Так як відношення рівнопотужності має властивості рефлективності, симетричності і транзитивності, то воно є відношенням еквівалентності.

Рівнопотужні множини можуть бути як скінченними так і нескінченними. Якщо множини скінченні і рівнопотужні, то вони мають однакову кількість елементів. Якщо множини Х та Y скінченні і множина Х рівнопотужна множині Y, то .

Якщо множини нескінченні і рівнопотужні, то частина множини може бути рівнопотужною всій множині.

Наприклад. 1) Множина А = {1,2,3,4}, множина букв у слові «урок», множина, що містить чотири геометричні фігури – все це рівнопотужні множини. Вони містять однакову кількість елементів.

2) Множина натуральних чисел і її підмножина – множина непарних натуральних чисел. Поставимо у відповідність кожному натуральному числу n непарне число 2n – 1. Ця відповідність взаємно однозначна: кожному натуральному числу відповідає єдине непарне число і кожне непарне число відповідає єдиному натуральному числу. Отже, 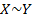, тобто множина натуральних чисел і множина непарних натуральних чисел, яка є підмножиною множини натуральних чисел, рівнопотужні.

Довгий час вважали, що всі нескінченні множини рівнопотужні між собою. В 70-80-х роках XIX ст. видатний німецький математик Г.Кантор (1845-1918) встановив, що серед нескінченних множин є безліч нерівнопотужних між собою множин і що всі нескінченні множини також можна розбити на класи рівнопотужних множин.

Найменша нескінченна потужність – це потужність множини натуральних чисел.

Будь-яка множина називається зчисленною, якщо вона рівнопотужна множині натуральних чисел.

Наприклад: множина усіх квадратів натуральних чисел називається зчисленною, бо вона рівнопотужна множині натуральних чисел. Множина усіх натуральних чисел, кратних k, множина цілих чисел, множина раціональних чисел також зчисленні. Між ними і множиною натуральних чисел можна встановити взаємно однозначну відповідність.

Г.Кантор довів, що множина дійсних чисел на відрізку не рівнопотужна множині натуральних чисел N і має більшу потужність, ніж потужність множини N.

Користуючись поняттям рівнопотужності множин, можна уточнити поняття скінченної і нескінченної множин.

Означення.Множина А називається скінченною, якщо в ній жодним способом не можна виділити правильної частини В, рівнопотужної всій множині А. Якщо в А можна виділити рівнопотужну їй правильну частину В, то тоді А називається нескінченною множиною.

Це означення розкриває найхарактернішу відмінність між скінченними й нескінченними множинами. Не слід ототожнювати нескінченну множину і скінченну множину, яка містить дуже багато елементів.

Питання для самоконтролю

1. Наведіть приклади множин, назвіть їх елементи.

2. Дайте означення порожньої множини, підмножини, рівних множин. Наведіть приклади.

3. Перелічіть відомі числові множини.

4. Дайте означення доповнення підмножини до множини.

5. Дайте означення перерізу множин, їх об’єднанню. Сформулюйте закони цих операцій.

6. Сформулюйте умови правильної класифікації. Наведіть приклади класифікацій.

7. Дайте означення декартового добутку двох множин. Поясніть зображення декартового добутку двох числових множин на координатній площині.

8. Сформулюйте означення відповідності між множинами. Перелічіть способи задання відповідностей.

9. Дайте поняття відповідності, оберненій до даної, назвіть її особливості.

10. Сформулюйте поняття взаємно однозначної відповідності.

11. Які множини називаються рівнопотужними?

12. Дайте означення бінарного відношення між елементами однієї множини, назвіть способи задання бінарних відношень.

13. Назвіть властивості бінарних відношень, проілюструйте на конкретних прикладах.

14. Що називається графом відношенням? Назвіть його елементи і позначення.

15. Яке відношення називається відношенням еквівалентності, відношенням порядку, відношенням нестрогого порядку? Наведіть приклади.

Читайте також:

1. Бюджетні множини й лінії бюджетного обмеження
2. Визначення загальної множини компонентів
3. Визначення множини допустимих планів задачі ЛП
4. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
5. Властивості множини невід’ємних раціональних чисел.
6. Властивості множини цілих невід’ємних чисел
7. Властивості множини цілих чисел.
8. Елементи множини
9. Залишки форм двоїни /у значенні множини/ в сучасній українській мові
10. Знову рахуємо підмножини
11. Зчисленні множини
12. Зчисленні множини

Переглядів: 7094