• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

II. СТРУКТУРА ТА ОБСЯГ КУРСОВОЇ РОБОТИ

Структура курсової роботи в чіткій послідовності має включати наступні компоненти:

– титульний аркуш (Додаток Б);

– завдання на курсову (дипломну) роботу (Додаток В);

– реферат (Додаток Г);

– зміст (Додаток Д);

– перелік умовних скорочень (якщо необхідно);

– вступ (Додаток К);

– основна частина (РОЗДІЛ 1, РОЗДІЛ 2);

– висновки;

– список використаних джерел;

– додатки.

Обсяг курсової роботи повинен складати 45 – 50 сторінок.

Реферат призначений для ознайомлення із курсовою роботою і повинен відповідати вимогам державних стандартів. Він має бути стислим, інформативним і містити відомості, які дозволяють прийняти рішення про доцільність читання всієї курсової роботи.

Реферат належить виконувати обсягом не більш, як 500 слів, i, бажано, щоб він уміщувався на сторінці формату А4. Він містить відомості про обсяг роботи, кількість ілюстрацій, таблиць, додатків, використаних джерел, на які є посилання в текстовому документі (включаючи дані додатків), текст реферату (визначення актуальності теми роботи, мети, предмету, об’єкта і методів дослідження; значимість роботи) та перелік ключових слів.

Ключові слова, що є визначальними для розкриття суті курсової роботи, вміщують після тексту реферату. Перелік ключових слів містить від 5 до 15 слів (словосполучень), надрукованих великими літерами в називному відмінку в рядок через коми.

Зміст розташовують безпосередньо після реферату, починаючи з нової сторінки; містить найменування та номери початкових сторінок усіх структурних частин роботи. До змісту включають перелік умовних скорочень (за необхідністю); вступ; назви та номери розділів, назви та номери підрозділів та пунктів; висновки; список використаних джерел; додатки. Підкреслення найменувань не допускається. Зверніть увагу на складний (розширений) зміст.

Основна частина складається з двох розділів.

Вступ до роботи. Коротко викладають оцінку сучасного стану проблеми; обґрунтовують актуальність та новизну теми роботи; мету роботи; завдання курсової роботи відповідно до визначеної мети дослідження; методи дослідження та інформаційні джерела.

Чітка постановка певної проблеми дозволяє студенту зосередити увагу на її вирішенні і не відволікатися на другорядні питання. Тому курсова робота повинна мати конкретно визначену мету дослідження.

Об’єкт дослідження – це частина реальної дійсності, яка підлягає дослідженню, тобто процес або явище, що породжує проблемну ситуацію.

Предмет дослідження міститься в межах об’єкта і конкретизує, що саме в об'єкті буде вивчатись.

Об’єкт і предмет дослідження, як категорії наукового процесу співвідносяться між собою як загальне і часткове. В об’єкті виділяється та його частина, яка є предметом дослідження. Саме на нього спрямована основна увага автора курсової роботи, оскільки предмет дослідження визначає тему роботи, що зазначається на титульному аркуші як її назва.

Мета розкриває, що саме автор прагне отримати в результаті дослідження: встановити залежності між чинниками; визначити зв’язки між явищами; розробити умови для усунення недоліків; розкрити можливості вдосконалення процесу; охарактеризувати обставини; простежити розвиток тощо.

Мета дослідження полягає у встановленні, виявленні наукових фактів, формулюванні закономірностей, обґрунтуванні найбільш ефективних шляхів дослідження. Тому в ній вживаються такі терміни: “визначити”, “дослідити”, “виявити”, “встановити”, “обґрунтувати”, “довести”, “перевірити”, "розробити" тощо.

Для досягнення мети формулюються локальні завдання дослідження, які в сукупності представляють собою комплексне вирішення проблеми. Завдання роботи формалізуються в назвах розділів та пунктів курсової роботи.

Окрім зазначеного, у вступі курсової роботи вказуються методи дослідження, що підтверджує об'єктивність виконуваного аналізу та наукову обґрунтованість висновків курсового дослідження. Також необхідно відзначити коло літературних джерел, джерел статистичної або звітної інформації, нормативних та законодавчих актів, які було використано при проведені дослідження. Обсяг вступу повинен складати 2 повних сторінки.

Основна частина курсової роботи складається з двох розділів. Теоретичні розділи повинні розкривати тему роботи, дотримуючись основних методологічних принципів: історичний підхід до аналізу економічних явищ і процесів; єдність історичного та логічного; системний, функціональний, динамічний, предметний та процесний підходи у дослідженні; нерозривний зв'язок теорії з практикою.

Завдання практичного розділу - дослідження динаміки об'єкта дослідження з обґрунтуванням та побудовою економіко-математичної моделі, проведення на її підставі розрахунків, підтвердження висновків теоретичних розділів.

Перший розділ – це теоретичні основи проблеми, яка розглядається. Він виконується на основі вивчення літературних джерел. Включає питання, які розкривають найважливіші теоретичні аспекти проблеми. Значення теоретичного розділу полягає в тому, щоб розкрити економічну сутність проблеми. Його завдання - глибоко дослідити теоретичну суть поставленої проблеми (процесу чи явища).

Обсяг першого розділу 40 - 50 % обсягу основного тексту роботи. Рекомендується оперувати теорією, виходячи з конкретних ситуацій, випадків тощо.

Крім теоретичних положень перший розділ повинен включати:

- аналіз об'єкта дослідження;

- обґрунтування напрямку подальшого вирішення проблем, які охоплює тема;

- обґрунтування напрямків та математичних методів дослідження з урахуванням виявлених особливостей об'єкта дослідження.

Цей розділ призначений для формулювання та опису теоретичних засад щодо вирішення задачі (задач) дослідження. Потрібно розглянути існуючі підходи, моделі, алгоритми, методики щодо їх розв’язання.

Для проведення дослідження виконується деталізація сутності новизни підходу (модифікація чи адаптація) запропонованих моделей для проведення дослідження з вказівкою сутності модифікації або адаптації методу або моделі, що пропонується.

В розділі потрібно розробити алгоритми розв’язання завдань роботи в рамках вирішуваної наукової проблеми та опис їх основних модулів, включаючи аналіз використання існуючих методологій застосування інструментальних засобів моделювання з використанням інформаційних технологій, систем та методів.

Теоретичні положення першого розділу мають бути застосовані для формулювання постановки завдань дослідження та покладені в основу другого розділу.

Перелік питань, що підлягають висвітленню, узгоджується з науковим керівником курсової роботи.

Основний обсяг посилань на використані джерела повинен міститись у першому розділі.

Другий розділ - (50 - 60 % обсягу основного тексту роботи) - це практична розробка за обраною моделлю чи методом дослідження операцій.

В розділі повинно бути відображено експериментальне дослідження теоретичних результатів на основі методів економічної кібернетики, за допомогою програмних пакетів (або створеного програмного продукту).

В підрозділі 2.1 необхідно:

- надати загальну характеристику підприємства (де знаходиться, скільки років працює, основна продукція чи послуга), чи є прибутковим (дослідження динаміки чистого прибутку, чистого доходу, майна підприємства та ін.), динаміка основних показників (від 3 років, при необхідності за темою – більше) та обґрунтування напрямку подальшого вирішення проблем, які охоплює тема. Аналіз показників підприємства у розрізі теми і постанова задачі (запис її у формальному вигляді – математичними формулами або графічно та ін. );

- описати метод моделювання на основі запропонованих теоретичних моделей, припущень та обмежень їх застосування;

- описати процес підготовки початкових даних.

В підрозділі 2.2 необхідно:

- привести оцінки адекватності запропонованих моделей та їх використання при моделюванні завдань дослідження;

- провести розрахунок оцінок адекватності на основі програмних пакетів (розробленого програмного продукту) та пакетів статистичної обробки даних.

В підрозділі 2.3 необхідно:

- провести аналіз ефективності запропонованих методів (алгоритмів) на основі обраних метрик: часових характеристик, оцінки складності алгоритмів, рівня адекватності моделі на основі статистичних показників;

- описати можливість та особливості практичної реалізації результатів дослідження.

В 2 розділі студентом повинні бути використані на практиці різні методи моделювання.

Моделювання – це побудова (або вибір) і вивчення такого об’єкта будь-якої природи (моделі), що здатний замінити собою досліджуваний об’єкт (оригінал) і вивчення якого дає нову інформацію про досліджуваний об’єкт. Формалізація опису задачі (об’єкта) здійснюється за допомогою знакових моделей (з використанням мови, схем, креслення, формул тощо). Найбільш важливим випадком знакового моделювання – математичне моделювання.

Математичне моделювання ґрунтується на математичній подібності, за якої виявляється відповідність схожих параметрів процесів різної фізичної природи, що порівнюються між собою. Знакову модель з використанням математики можна описати різними способами: аналітично (у вигляді заданих функціональних співвідношень, диференціальних, інтегральних, різницевих рівнянь тощо), алгоритмічно, графічно і т. п.

Математичними уявними моделями можна вважати алгоритми й програми, розроблені для обчислювальних машин, які в умовних знаках відбивають (моделюють) певні процеси, що описані диференціальними рівняннями, покладеними в основу алгоритмів, а також різні структурні схеми, які відображають функціональні зв’язки між підсистемами складних систем. Усі види таких математичних формалізацій можуть бути зведені до математичної моделі. Типи моделей можуть бути або детермінованими (відображають детерміновані процеси з однозначно визначеними причинами та їх наслідками), або стохастичними (відображають імовірнісні події). Для представлення знакових моделей використовують такі основні форми:

1. Інваріантна форма – це запис співвідношень моделі за допомогою традиційної математичної мови безвідносно до методу розв’язання рівняння моделі.

2. Алгоритмічна форма – це запис співвідношень моделі й обраного чисельного методу вирішення у формі алгоритму.

3. Аналітична форма – це запис моделі у вигляді результату аналітичного вирішення вихідних рівнянь моделі. Як правило, моделі в аналітичній формі являють собою явні вирази вихідних параметрів як функцій внутрішніх і зовнішніх параметрів.

4. Схемна форма. Інакше її називають графічною формою. Це представлення моделі на деякій графічній мові (наприклад, мові графів, еквівалентних схем, діаграм і т.д.). Використання таких форм можливо при наявності правил однозначного тлумачення елементів креслень і їх перекладу на мову інваріантних або алгоритмічних форм.

Моделі в алгоритмічній і аналітичній формах називають відповідно алгоритмічними й аналітичними. Серед алгоритмічних моделей важливий клас становлять імітаційні моделі, призначені для імітації фізичних чи інформаційних процесів в об'єкті при визначенні різних залежностей вхідних впливів від часу. Імітацію названих процесів називають імітаційним моделюванням. Результат імітаційного моделювання – залежності фазових змінних в обраних елементах системи від часу. Імітаційні моделі реалізують на ПК у вигляді моделюючих алгоритмів (програм), що дозволяють обчислити значення вихідних характеристик і визначити новий стан, у якому знаходиться модель при заданих значеннях вхідних змінних, параметрів і початковому стані моделі.

Структурні моделі відтворюють склад елементів об'єкта, системи, явища і взаємозв'язку між ними, тобто структуру об'єкта моделювання.

Функціональні моделі імітують спосіб поведінки оригіналу, його функціональну залежність від зовнішнього середовища.

Аналітичні моделі дозволяють одержати явні залежності необхідних величин від змінних і параметрів, що характеризують явище. Аналітичний розв'язок математичного співвідношення є узагальненим описом об'єкта.

Числові моделі характеризуються тим, що значення необхідних величин можна одержати в результаті застосування кількісних методів. Усі кількісні методи дозволяють одержати тільки часткову інформацію щодо досліджуваних величин, тому що для своєї реалізації потребують завдання всіх параметрів, які входять до математичного співвідношення.

За поведінкою в часі моделі бувають:

- динамічними (час відіграє роль незалежної змінної, а поведінка об'єкта моделювання змінюється в часі);

- статичними (поведінка об'єкта моделювання не залежить від часу);

- квазістатичними (поведінка об'єкта моделювання змінюється з одного статичного стану на інший відповідно до зовнішніх впливів).

Процес математичного моделювання включає наступні основні етапи:

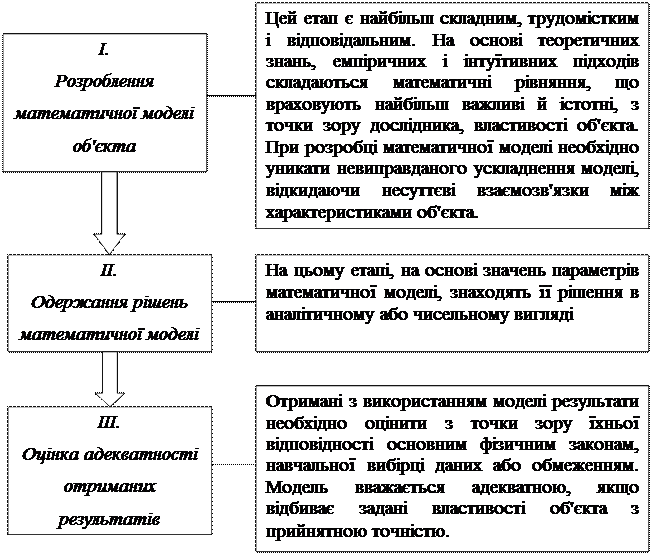
Точність визначається як ступінь збігу значень вихідних параметрів моделі й об'єкта. Пояснимо сказане.

Нехай ξj – відносна похибка моделі по j-му вихідному параметру:

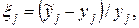
(1)

де 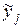- j-й вихідний параметр, розрахований за допомогою моделі;

- той же вихідний параметр, що має місце в об'єкті, який моделюється.

Похибка розрахунку ξМ за сукупністю вихідних параметрів, що враховуються однією з норм вектора. Наприклад:

(2)

або

(3)

В загальному випадку точність моделі різна в різних умовах функціонування об'єкта. Ці умови характеризуються зовнішніми параметрами. Якщо задатися граничною припустимою похибкою ξгп, то можна в просторі зовнішніх параметрів виділити область, в якій виконується умова

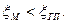
(4)

Цю область називають областю адекватності моделі (ОА). У разі потреби індивідуальні граничні значення ξгпj для кожного вихідного параметра і визначають область адекватності, в якій одночасно виконуються всі m умов вигляду

(5)

При побудові математичних моделей використовують, як правило, наступні методи:

1. Методи математичного програмування для рішення задач оптимізації.

2. Методи імітаційного моделювання.

3. Статистичні методи для рішення задач регресійного аналізу, кластеризації, класифікації.

4. Методи та моделі штучного інтелекту (наприклад, нейроні мережі).

Методи математичного програмування. Складну систему можна схематично подати у вигляді прямокутника (рис. 1):

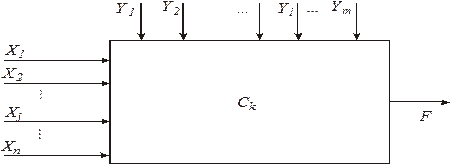
Рис. 1. Опис системи, яка моделюється

Параметри є кількісними характеристиками системи.

Кількісні характеристики є змінними величинами, які бувають незалежними чи залежними, дискретними або неперервними, детермінованими або випадковими. Незалежні змінні бувають двох видів: керовані , значення яких можна змінювати в деякому інтервалі; некеровані змінні , значення яких не залежать від волі людей і визначаються зовнішнім середовищем.

Кожна економічна система має мету (ціль) розвитку та функціонування. Це може бути, наприклад, отримання максимуму чистого прибутку. Ступінь досягнення мети, здебільшого, має кількісну міру, тобто може бути описаний математично.

Нехай F — обрана мета (ціль). За цих умов вдається, як правило, встановити залежність між величиною F, якою вимірюється ступінь досягнення мети, і незалежними змінними та параметрами системи:

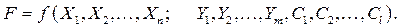
(6)

Функцію F називають цільовою функцією, або функцією мети. Для економічної системи це є функція ефективності її функціонування та розвитку, оскільки значення F відбиває ступінь досягнення певної мети.

Постановка задачі математичного програмування формулюється наступним чином:

Знайти такі значення керованих змінних Хj щоб цільова функція набувала екстремального (максимального чи мінімального) значення.

Отже, потрібно відшукати значення

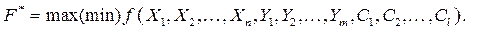
(7)

Можливості вибору Xj завжди обмежені зовнішніми щодо системи умовами, параметрами виробничо-економічної системи і т. ін.

Процеси можливо описати системою математичних рівностей та нерівностей виду

(8)

Набір символів означає, що для деяких значень поточного індексу r виконуються нерівності типу £, для інших — рівності (=), а для решти — нерівності типу ³.

Система (8) називається системою обмежень, або системою умов задачі. Вона описує внутрішні технологічні та економічні процеси функціонування й розвитку виробничо-економічної системи, а також процеси зовнішнього середовища, які впливають на результат діяльності системи. Для економічних систем змінні Xj мають бути невід'ємними:

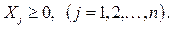
При розробленні економіко-математичної моделі для рішення задач оптимізації, слід керуватися певними правилами:

1. Модель має адекватно описувати реальні технологічні та економічні процеси.

2. У моделі потрібно враховувати тільки суттєве в досліджуваному явищі чи процесі.

3. Модель має бути зрозумілою для користувача, зручною для реалізації на ПК.

4. Потрібно забезпечити, щоб множина наборів Хj була не порожньою. Будь-який набір змінних , що задовольняє умови (7) і (8), називають допустимим рішенням, або планом. План, за якого цільова функція набуває екстремального значення, називається оптимальним.

Імітаційне моделювання ­ особлива форма проведення експериментів на ЕОМ з математичними моделями, які з певним ступенем ймовірності описують закономірності функціонування реальних систем і об’єктів.

Суть імітаційного моделювання у тому, що досліджувана динамічна система заміняється її імітатором і з ним проводяться експерименти. Призначення імітаційних експериментів – одержати інформацію про досліджувану систему. У процесі імітаційного моделювання відтворюються явища, які описані математичною моделлю, зі збереженням їхньої логічної структури і послідовності чергування в часі. Рівень деталізації імітаційної моделі може бути різним (залежно від поставлених цілей), що спрямовано на одержання потрібних характеристик. Імітаційні (алгоритмічні) моделі можуть бути детермінованими і стохастичними. В останньому випадку за допомогою датчиків (генераторів) випадкових чисел імітується вплив (дія) невизначених і випадкових чинників. Такий метод імітаційного моделювання дістав назву методу статистичного моделювання (статистичних прогонів, чи методу Монте-Карло). На даний час цей метод вважають одним із найефективніших методів дослідження складних систем, а часто і єдиним практично доступним методом отримання нової інформації щодо поведінки гіпотетичної системи (на етапі її проектування).

Рекомендуються наступні інструментальні засоби імітаційного моделювання:

Система імітаційного моделювання GPSS. Це потужне середовище комп'ютерного моделювання загального призначення, розроблене для професіоналів в області моделювання.

ARIS. Комплексний моделюючий інструмент, що охоплює області як дискретного, так і безперервного комп'ютерного моделювання, що має високий рівень інтерактивності й візуального подання інформації.

Пакет прикладних програм MATLAB . Інструмент призначений для рішення завдань технічних обчислень. Включає мову програмування.

Система ARENA компанії Systems Modeling. Система дозволяє будувати імітаційні моделі, програвати їх і аналізувати результати імітаційного моделювання.

Статистичні методи. Інструменти статистичного аналізу: Statistica, SPSS, Excel, MatLab, MatCad.

Регресійний аналіз - метод статистичного аналізу для визначення залежності випадкової величини від змінних 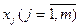, розглянутих у регресійному аналізі як невипадкові величини, незалежно від істинного закону розподілу 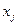. В загальному вигляді модель записується наступним чином:

Оцінку параметрів регресії можна провести багатьма методами, зокрема методом найменших квадратів.

Для оцінки підібраної лінійної моделі використовують множинний коефіцієнт кореляції та коефіцієнт детермінації . Чим ближче значення і 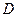наближаються до 1, тим кращою є побудована модель (рис. 2). Для оцінки значущості параметрів моделі і моделі в цілому використовуються критерій Стьюдента і критерій Фішера.

Рис. 2. Оцінка адекватності моделі множинної регресії

Multiple R – коефіцієнт множинної кореляції, який характеризує тісноту лінійного зв'язку між залежною й всіма незалежними змінними. Цей коефіцієнт може приймати значення від 0 до 1. Чим ближче цей коефіцієнт до 1, тим кращою є побудована модель.

R2 або RI – коефіцієнт детермінації, який чисельно виражає частку варіації залежної змінної, пояснену за допомогою регресійного рівняння. Чим більше R2, тим більшу частку варіації пояснюють змінні, включені в модель.

adjusted R – скоректований коефіцієнт множинної кореляції. Цей коефіцієнт позбавлений недоліків коефіцієнта множинної кореляції. Включення нової змінної в регресійне рівняння збільшує RI не завжди, а тільки в тому випадку, коли частинний F-критерій при перевірці гіпотези про значущість включеної змінної більше або дорівнює 1. У противному випадку включення нової змінної зменшує значення RI й adjusted R2.

Кластерний аналіз – це сукупність методів, що дозволяють класифікувати, багатомірні спостереження, кожне з яких описується набором вихідних змінних 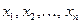. Метою кластерного аналізу є утворення груп схожих між собою об'єктів, які прийнято називати кластерами. На відміну від комбінаційних угруповань кластерний аналіз приводить до розбивки на групи з урахуванням всіх групувальних ознак одночасно.

Методи кластерного аналізу дозволяють:

- провести класифікацію об'єктів з урахуванням ознак, що відбивають сутність, природу об'єктів. Рішення такої задачі, як правило, призводить до поглиблення знань про сукупності класифікованих об'єктів;

- перевірити висунуті припущення про наявність деякої структури в досліджуваній сукупності об'єктів, тобто пошук існуючої структури;

- побудувати нові класифікації для слабоформалізованих явищ, коли необхідно встановити наявність зв'язків усередині сукупності й спробувати привнести в неї структуру.

До основних характеристик кластеризації належать: середнє значення, стандартне відхилення та варіація для кожного показника (змінної) в кожному кластері, кількість елементів, що ввійшли в кожен кластер (рис. 3).

Рис. 3. Оцінка характеристик кластеризації

Дерева рішень (класифікації) – це метод, що дозволяє передбачати приналежність спостережень або об'єктів до того або іншого класу категоріальної залежної змінної відповідно до значень однієї або декількох предикторних (передбачувальних, незалежних) змінних. Ієрархічна будова "дерева класифікації" – одна з найважливіших його властивостей. "Стовбуром дерева" є проблема або ситуація, яка вимагає рішення. "Вершиною дерева" є цілі або цінності, якими керується людина, що ухвалює рішення (рис. 4).

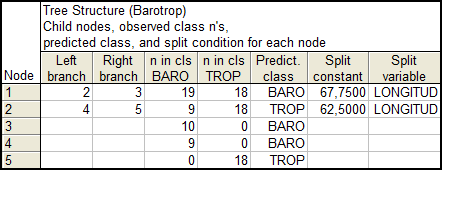
Рис.4. Оцінка характеристик класифікації

Штучні нейроні мережі. Нейроні мережі дозволяють отримати структурну модель для моделювання значення цільового вихідного показника на основі використання набору вхідних змінних, математичних функцій активації та вагових коефіцієнтів вхідних параметрів. В процесі навчання виконується ітеративний навчальний цикл (здійснюється модифікація вагових коефіцієнтів). Пакети, які реалізують нейроні мережі, - SNN, NeuroShell, NeuroSolution, MatLab. На рис. 5. показані результати навчання нейронної мережі та критерії оцінки її адекватності.

Рис. 5. Характеристики нейронної мережі

Колонка Type відображає тип мережі: MLP (багатошаровий персептрон), RBF (радіальна мережа), Linear (лінійна мережа), PNN (імовірнісна мережа), GRNN (узагальнена регресійна мережа).

Inputs – кількість вхідних змінних в мережі.

Hidden, Hidden(2) – кількість прихованих елементів в мережі (або «-», якщо мережа не має прихованих елементів).

Кількість прихованих елементів разом з кількістю входів визначають складність мережі.

Колонка Training містить умовні позначення про три останні алгоритми, які використовувалися для навчання мережі. Наприклад BP50bsс означає: BP – для навчання мережі використовувався алгоритм зворотного поширення помилки (Back Propagation), при навчанні було пройдено 50 епох, s – виконалася умова останову і було витрачено менше епох ніж задавалося спочатку, b – мережа є кращою в мережевому наборі, с – відбулася збіжність алгоритму (був досягнутий локальний або глобальний мінімум).

Колонки TPerf, VPerf, TePerf показують продуктивність мережі (коефіцієнт S.D.Ratio) на тренувальному, перевірочному і тестовому наборах відповідно. Колонки TError, VError, TeError показують середньоквадратичну помилку роботи мережі на тренувальному, перевірочному і тестовому наборах відповідно. Значні відмінності в їх значеннях вказують на ненадійність оцінки продуктивності мережі.

Вибір методу рішення задачі визначається сутністю задачі, її приналежністю до відповідного класу (оптимізації, кластеризації, прогнозування, аналізу часових рядів, класифікації, розпізнавання образів.

При виборі моделі студент повинен:

1. Визначити задачу (або предмет дослідження), для якої необхідно використати математичні моделі, методи (підходи, інструменти). Стисло визначити (описати) клас задачі (задач) (наприклад, задачі обліку, прогнозування, кластеризації, регресії, оптимізації, імітаційного моделювання, агрегації, описової статистики та інше).

2. Визначити та чітко уявляти результат моделювання (рішення задачі). Треба описати, що необхідно отримати в якості результату при використанні математичного апарату (наприклад, групування даних, оптимальне значення цільової функції та її параметрів (змінних), результат функціоналу, координати об’єкта та інше).

3. Визначити критерії оцінки адекватності результату (наприклад, статистичні – рівень відносної помилки, рівень коефіцієнту детермінації) або інших критеріїв (наприклад, час отримання результату, точність розрахунку).

4. Визначити умови та фактори (змінні), які необхідно використати при розробленні математичної моделі - опису функціоналу, набору правил, обмежень. Стисло описати фактори, дані та умови, які необхідно використати для розрахунків в моделі (задачі).

5. Визначити навчальну вибірку (або початкові дані) для процесу моделювання, або для побудови моделі. Відсутність даних щодо показників не дає змогу їх використовувати в моделі (наприклад, статистичної). Обсяг даних, як правило, залежіть від кількості обраних показників у моделі.

6. Вибрати (визначити, описати) метод або математичний апарат, який необхідно використати для рішення задачі (наприклад, методи математичної статистики, штучного інтелекту, теорії графів, лінійного або нелінійного програмування та інше). Вибір методу залежіть від наявності статистичних даних, результатів моделювання, критеріїв оцінки результатів моделювання.

7. Навести опис математичної моделі в термінах, які будуть використані для побудови алгоритму або опису програмної реалізації моделі. При опису моделі необхідно пояснити кожен ідентифікатор (компонент), який використовується в моделі.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. I 9. Структура речевого дефекта у детей,
3. I. Аналіз контрольної роботи.
4. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
5. II. Вимоги безпеки перед початком роботи
6. II. Вимоги безпеки праці перед початком роботи
7. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
8. III ОФОРМЛЕННЯ І ЗАХИСТ РОБОТИ
9. III. Вимоги безпеки під час виконання роботи
10. III. Вимоги безпеки під час виконання роботи
11. III. Вимоги безпеки під час виконання роботи

Переглядів: 4359