• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Диференціювання та інтегрування матриць.

Кронекеровий добуток прямокутних матриць.

Ця операція може виконуватися над прямокутними матрицями будь-яких розмірів. Кронекеровий добуток (m ´ n ) - матриці А на (p ´ q) - матрицю В позначається А Ä В та виражається матрицею розміру

(mp Ä nq):

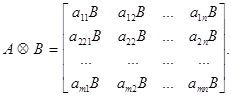
Можна показати, що при існуванні звичайних матричних добутків АС і BD справедливо співвідношення: (A Ä B)(C Ä D) = AC Ä BD. Має місце також наступні властивості кронекерового добутку:

(A Ä B)^t = A^t Ä B^t; (A Ä B)^-1 = A^-1 Ä B^-1.

Розглядаючи диференціальне рівняння у матричній формі, маємо справу з елементами які є не числа, а функції від скалярного аргументу (часу t або будь-якої іншої змінної). Диференціювання і інтегрування таких матриць зводиться до правил, аналогічним звичайним правилам диференціювання і інтегрування з однією суттєвою відмінністю. Так як добуток матриць в загальному випадку некомутативний, то необхідно слідкувати за збереженням початкового порядку послідовних сполучень.

Нехай матриця X(t) розміром (m´n) має своїми елементами диференційовані функції x_ij(t) скалярного аргументу t. Похідна матриці X(t) за змінною t визначається як

,

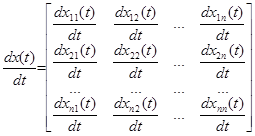тобто диференціювання матриці зводиться до диференціювання усіх її елементів по тій же змінній. Має місце також співвідношення:

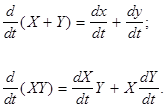
Якщо у першому з приведених співвідношень порядок послідовності матриць та їх похідних байдужий, то у другому він повинен бути строгою.

Якщо матриця X(t) - диференційована і має обернену X^-1(t), то похідна від оберненої матриці визначається співвідношенням:

.
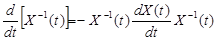Тема 4. Матриці. Визначник матриць.

Читайте також:

1. Безпосереднє інтегрування
2. Диференціювання неявних функцій
3. Диференціювання складних функцій
4. Додавання матриць.
5. Інтегрування виразів, що містять тригонометричні функції
6. Інтегрування господарства економіки України до у світовий економічний простір
7. Інтегрування деяких ірраціональних функцій
8. Інтегрування деяких тригонометричних функцій
9. Інтегрування і пониження порядку деяких ДР з вищими похідними.
10. Інтегрування ірраціональних функцій
11. Інтегрування найпростіших раціональних дробів

Переглядів: 2342