Ізокванта

Розглянемо варіант, коли змінними є два фактори виробництва (наприклад, праця і капітал), що при визначеному співвідношенні дають у результаті однаковий обсяг виробленого продукту. Наприклад, візьмемо витрати праці і капіталу при виробництві взуття. Витрати праці позначимо Х, а витрати капіталу – Y. При визначеній комбінації цих двох факторів може бути вироблено 200 пар взуття (Q = 200). Зміна капіталу і праці може відбуватися в різних напрямках. Якщо кількість капіталу збільшується, то застосування праці зменшується, при цьому загальний обсяг виробництва не змінюється. Цю залежність можна представити графічно з використанням ізокванти (кривої рівного обсягу випуску).

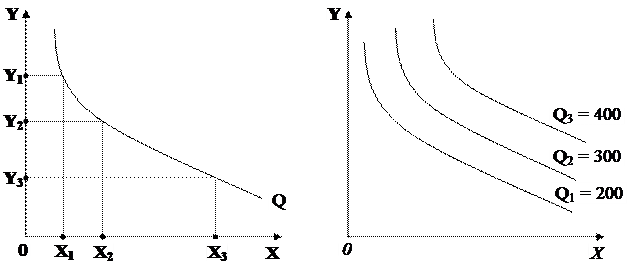
Ізокванта – крива, на якій розташовані всі співвідношення факторів, використання яких дає однаковий обсяг випуску продукції (рис. 6.3). При збільшенні обсягів факторів відбувається збільшення обсягу випуску продукції. Ізокванта, що показує виробництво більшого обсягу продукту, буде розташована праворуч і вище попередньої. Ізокванти, що відповідають різним обсягам продукції, утворюють карту ізоквант (рис. 6.4).

Рис. 6.3 - Ізокванта

Рис. 6.4 - Карта ізоквант

Ізокванти мають негативний нахил. Це пояснюються тим, що збільшення використання одного фактора (при визначеному обсязі випуску продукту) можливе тільки при зменшенні іншого фактора. Показником такої зміни співвідношення факторів є гранична норма технологічного заміщення факторами виробництва один одного.

Гранична норма технологічного заміщенняпрацею капіталу (MRTS_LК) – розмір капіталу, який може замінити кожна додаткова одиниця праці без зміни обсягу випуску продукції.

Гранична норма технологічного заміщення фактора Y фактором Х розраховується як відношення зміни обсягів їх використання. MRTS_x,y береться зі знаком мінус, тому що заміна факторів відбувається в зворотному напрямку:

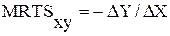
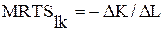Якщо ми візьмемо яку-небудь точку на ізокванті, наприклад, точку А (рис. 6.5), і проведемо до неї дотичну КМ, то тангенс кута a дасть нам значення MRTS_x,y = tg a.

Ізокванти випуклі до початку координат.У верхній частині ізокванти кут a буде досить великим. Це означає, що для зміни фактора C на одиницю вимагаються значні зміни фактора Y. Отже, у цій частині кривої значення MRTS_x,y буде велике. В процесі руху вниз по ізокванті значення граничної норми технологічного заміщення буде поступово убувати. Це означає, що для збільшення фактора C на одиницю буде потрібно незначне зменшення фактора Y.

MRTS_x,y зв'язана з граничною продуктивністю факторів виробництва:

а) приріст випуску продукції можливий за рахунок збільшення використання капіталу (К – вісь Y): DQ_K = MP_K´DK;

б) за рахунок збільшення використання праці (L–вісь X): DQ_L= MP_L´DL;

в) у рамках однієї ізокванти приріст випуску дорівнює нулю (обсяг виробництва не змінюється), тому:

DQ_К + DQ_L = MP_К´DK + MP_L´DL = 0 Þ MP_К´DK = - MP_L´DL 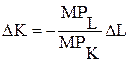Þ

Þ .

Можна зробити висновок, що гранична норма технологічного заміщення визначається співвідношенням граничних продуктів факторів виробництва.

У реальних виробничих процесах зустрічаються два виняткові випадки в конфігурації ізоквант:

1) два фактори ідеально взаємозамінні (рис. 6.6) MRTS_x,y = const;

2) два фактори жорстко доповнюють один одного (рис. 6.7).

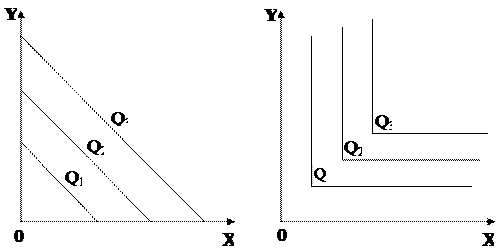Рис. 6.6 - Ізокванта при повній Рис. 6.7 - Ізокванта при твердій взаємозаміні факторів доповнюваності факторів

Читайте також:

Ізокванта. Заміна факторів виробництва

<== попередня сторінка	\|	наступна сторінка ==>
Виробництво та виробнича функція	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.