Present your ideas on the given subject for the students' research society.

Let us first consider what theory tells us will be the ultimate fate of our sun. The sun has been in existence for some five thousand million years. In another 5-6 thousand million years it will begin to expand in size, swelling inexorably outwards until its surface reaches to about the orbit of the earth. It will then have become a type of star known as a red giant. Many red giants are observed elsewhere in the heavens, two of the best known being Aldebaran in Taurus and Betelgeuse in Orion. All the time that its surface is expanding, there will be, at its very core, an exceptionally dense small concentration of matter, which steadily grows. This dense core will have the nature of a white dwarf star (Fig. 1).

White dwarf stars, when on their own, are actual stars whose material is concentrated to extremely high density, such that a ping-pong ball filled with their material would weigh several hundred tonnes! Such stars are observed in the heavens, in quite considerable numbers: perhaps some ten per cent of the luminous stars in our Milky Way galaxy are white dwarfs. The most famous white dwarf is the companion of Sirius, whose alarmingly high density had provided a great observational puzzle to astronomers in the early part of this century. Later, however, this same star provided a marvellous confirmation of physical theory (originally by R. H. Fowler, in around 1926) – according to which, some stars could indeed have such a large density, and would be held apart by 'electron degeneracy pressure', meaning that it is Pauli's quantum-mechanical exclusion principle, as applied to electrons, that is preventing the star from collapsing gravitationally inwards.

Any red giant star will have a white dwarf at its core, and this core will be continually gathering material from the main body of the star. Eventually, the red giant will be completely consumed by this parasitic core, and an actual white dwarf – about the the size of the earth – is all that remains. Our sun will be expected to exist as a red giant for 'only' a few thousand million years. Afterwards, in its last 'visible' incarnation – as a slowly cooling dying ember1 of a white dwarf – the sun will persist for a few more thousands of millions of years, finally obtaining total obscurity as an invisible black dwarf.

Not all stars would share the sun's fate. For some, their destiny is a considerably more violent one, and their fate is sealed by what is known as the Chandrasekhar limit: the maximum possible value for the mass of a white dwarf star. According to a calculation performed in 1929 by Subrahmanyan Chandrasekhar, white dwarfs cannot exist if their masses are more than about one and one-fifth times the mass of the sun. (He was a young Indian research student-to-be, who was travelling on the boat from India to England when he made his calculation.) The calculation was also repeated independently in about 1930 by the Russian Lev Landau. The modern somewhat refined value for Chandrasekhar's limit is about 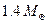where 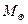is the mass of the sun, i.e. 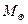= one solar mass.

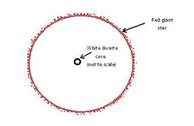
Fig. 1. A red giant star with a white dwarf core

Note that the Chandrasekhar limit is not much greater than the sun's mass, whereas many ordinary stars are known whose mass is considerably greater than this value. What would be the ultimate fate of a star of mass 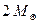, for example? Again, according to established theory, the star should swell to become a red giant, and its white-dwarf core would slowly acquire mass, just as before. However, at some critical stage the core will reach Chandrasekhar's limit, and Pauli's exclusion principle will be insufficient to hold it apart against the enormous gravitationally induced pressures. At this point, or thereabouts, the core will collapse catastrophically inwards, and hugely increased temperatures and pressures will be encountered. Violent nuclear reactions take place, and an enormous amount of energy is released from the core in the form of neutrinos. These heat up the outer regions of the star, which have been collapsing inwards, and a stupendous explosion ensues. The star has become a supernova!

What then happens to the still-collapsing core? Theory tells us that it reaches enormously greater densities even than those alarming ones already achieved inside a white dwarf. The core can stabilize as a neutron star , where now it is neutron degeneracy pressure – i.e. the Pauli principle applied to neutrons – that is holding it apart. The density would be such that our ping-pong ball containing neutron star material would weigh as much a the asteroid Hermes (or perhaps Mars's moon Deimos). This is the kind оf density found inside the very nucleus itself! (A neutron star is like a huge atomic nucleus, perhaps some ten kilometres in radius, which is, however, extremely tiny by stellar standards!) But there is now a new limit, analogous to Chandrasekhar's (referred to as the Landau-Oppenheimer-Volkov limit) whose modern (revised) value is very roughly 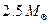, above which a neutron star cannot hold itself apart.

What happens to this collapsing core if the mass of the original star is great enough that even this limit will be exceeded? Many stars are known, of masses ranging between 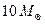and 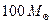, for example. It would seem highly unlikely that they would invariably throw off so much mass that the resulting core necessarily lies below this neutron star limit. The expectation is that, instead, a black hole will result.

What is a black hole? It is a region of space – or of space-time – within which the gravitational field has become so strong that even light cannot escape from it. Recall that it is an implication of the principles of relativity that the velocity of light is the limiting velocity: no material object or signal can exceed the local light speed. Hence, if light cannot escape from a black hole, nothing can escape.

Perhaps the reader is familiar with the concept of escape velocity. This is the speed which an object must attain in order to escape from some massive body. Suppose that body were the earth; then the escape velocity from it would be approximately 40000 kilometres per hour, which is about 25000 miles per hour. A stone which is hurled from the earth's surface (in any direction away from the ground), with a speed exceeding this value, will escape from the earth completely (assuming that we may ignore the effects of air resistance). If thrown with less than this speed, then it will fall back to the earth. (Thus, it is not true that 'everything that goes up must come down'; an object returns only if it is thrown with less than the escape velocity!) For Jupiter, the escape velocity is 220000 kilometres per hour i.e. about 140000 miles per hour; and for the sun it is 2200000 kilometres per hour, or about 1400000 miles per hour. Now suppose we imagine that the sun's mass were concentrated in a sphere of just one quarter of its present radius, then we should obtain an escape velocity which is twice as great as its present value; if the sun were even more concentrated, say in a sphere of one-hundredth of its present radius, then the velocity would be ten times as great. We can imagine that for a sufficiently massive and concentrated body, the escape velocity could exceed even the velocity of light! When this happens, we have a black hole.

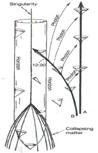
In Fig. 2, I have drawn a space-time diagram depicting the collapse of a body to form a black hole (where I am assuming that the collapse proceeds in a way that maintains spherical symmetry reasonably closely, and where I have suppressed one of the spatial dimensions). The light cones have been depicted, and, as we recall from the discussion of general relativity, these indicate the absolute limitations on the motion of a material object or signal. Note that the cones begin to tip inwards towards the centre, and the tipping gets more and more extreme the more central they are.

There is a critical distance from the centre, referred to as the Schwarzschild radius, at which the outer limits of the cones become vertical in the diagram. At this distance, light (which must follow the light cones) can simply hover above the collapsed body, aid all the outward velocity that the light can muster is just barely enough to counteract the enormous gravitational pull. The (3-)surface in space-time traced out, at the Schwarzschild radius, by this hovering light (i.e. the light's entire history) is referred to as the (absolute) event horizon of the black hole. Anything that finds itself within the event horizon is unable to escape or even to communicate with the outside world. This can be seen from the tipping of the cones, and from the fundamental fact that all motions and signals are constrained to propagate within (or on) these cones. For a black hole formed by the collapse of a star of a few solar masses, the radius of the horizon would be a few kilometres. Much larger black holes are expected to reside at galactic centres. Our own Milky Way galaxy may well contain a black hole of about a million solar masses, and the radius of the hole would then be a few million kilometres.


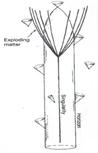
Fig. 2. A space-time diagram depicting collapse to a black hole. The Schwarzschild radius is marked ‘Horizon’	Fig. 3. A hypothetical space-time configuration: a white hole, ultimately exploding into matter (the time reverse of the space-time of Fig. 2)

The actual material body which collapses to form the black hole will end up totally within the horizon, and so it is then unable to communicate with the outside. We shall be considering the probable fate of the body shortly. For the moment, it is just the space-time geometry created by its collapse that concerns us – a space-time geometry with profoundly curious implications.

Let us imagine a brave (or foolhardy?) astronaut B, who resolves to travel into a large black hole, while his more timid (or cautious?) companion A remains safely outside the event horizon. Let us suppose that A endeavours to keep В in view for as long as possible. What does A see? It may be ascertained from Fig. 2 that the portion of B's history (i.e. B's world-line) which lies inside the horizon will never be seen by A, whereas the portion outside the horizon will all eventually have become visible to A – though B's moments immediately preceding his plunge across the horizon will be seen by A only after longer and longer periods of waiting. Suppose that В crosses the horizon when his own watch registers 12 o'clock. That occurrence will never actually be witnessed by A, but the watch-readings 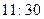, , 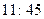, , 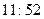, , 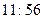, , 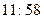, 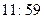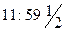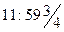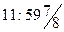etc. will be successively seen by A (at roughly equal intervals, from A's point of view). In principle, В will always remain visible to A and would appear to be forever hovering just above the horizon, his watch edging ever more slowly towards the fateful hour of 12:00, but never quite reaching it. But, in fact the image of В that is perceived by A would very rapidly become too dim to be discernible. This is because the light from the tiny portion of B's world-line just outside the horizon has to make do for the whole of the remainder of A's experienced time. In effect, В will have vanished from A's view – and the same would be true of the entire original collapsing body. All that A can see will indeed be just a 'black hole'!

What about poor B? What will be his experience? It should first be pointed out that there will be nothing whatever noticeable by В at the moment of his crossing the horizon. He glances at his watch as it registers around 12 o'clock and he sees the minutes pass regularly by: 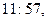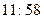, , 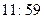, , 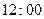, ,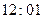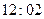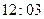… .Nothing seems particularly odd about the time 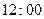. He can look back at A, and will find that A remains continuously in view the whole time. He can look at A's own watch, which appears to В to be proceeding forwards in an orderly and regular fashion. Unless В has calculated that he must have crossed the horizon, he will have no means of knowing it. The horizon has been insidious in the extreme. Once crossed, there is no escape for B. His local universe will eventually be found to be collapsing about him, and he will be destined shortly to encounter his own private' big crunch'!

Or perhaps it is not so private. All the matter of the collapsed body that formed the black hole in the first place will, in a sense, be sharing the 'same' crunch with him. In fact, if the universe outside the hole is spatially closed, so that the outside matter is also ultimately engulfed in an all-embracing big crunch, then that crunch, also, would be expected to be the 'same' as B's 'private' one.

Despite B's unpleasant fate, we do not expect that the local physics that he experiences up to that point should be at odds with the physics that we have come to know and understand. In particular, we do not expect that he will experience local violations of the second law of thermodynamics, let alone a complete reversal of the increasing behaviour of entropy. The second law will hold sway just as much inside a black hole as it does elsewhere. The entropy in B's vicinity is still increasing, right up until the time of his final crunch.

To understand how the entropy in a 'big crunch' (either 'private' or 'all-embracing') can indeed be enormously high, whereas the entropy in the big bang had to have been much lower, we shall need to delve a little more deeply into the space-time geometry of a black hole. But before we do so, the reader should catch a glimpse also of Fig. 3 which depicts the hypothetical time-reverse of a black hole, namely a white hole. White holes probably do not exist in nature, but their theoretical possibility will have considerable significance for us.

<== попередня сторінка	\|	наступна сторінка ==>
Text 5. Black Holes	\|	Text 6. Hawking's box: a link with the Weyl curvature hypothesis?

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.