Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Колебательное движение

1. Что такое колебания? свободные колебания? гармонические колебания? периодические процессы?

2. Дайте определения амплитуды, фазы, периода, частоты, циклической частоты колебания.

3. Какова связь амплитуды и фазы смещения, скорости и ускорения при прямолинейных гармонических колебаниях?

4. Запишите формулы для скорости и ускорения гармонически колеблющейся точки как функции времени.

5. Запишите и прокомментируйте формулы для кинетической, потенциальной и полной энергии при гармонических колебаниях.

6. Как можно сравнить между собой массы тела, измеряя частоты колебаний при подвешивании этих масс к пружине?

7. Что называется гармоническим осциллятором? пружинным маятником? физическим? математическим?

8. Запишите формулы для периодов колебаний пружинного, физического и математического маятников.

9. Что такое приведенная длина физического маятника?

10. Запишите и проанализируйте дифференциальное уравнение свободных гармонических колебаний в контуре.

11. Что такое биения? Чему равна частота биений? период?

12. Какова траектория точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях с одинаковыми периодами? Когда получается окружность? прямая?

13. Запишите дифференциальное уравнение затухающих колебаний и его решение. Проанализируйте их для механических и электромагнитных колебаний.

14. По какому закону изменяется амплитуда затухающих колебаний? Являются ли затухающие колебания периодическими?

15. Почему частота затухающих колебаний должна быть меньше частоты собственных колебаний системы?

16. Что такое коэффициент затухания? декремент затухания? логарифмический декремент затухания? В чем заключается физический смысл этих величин?

17. Что такое автоколебания? В чем их отличие от вынужденных и свободных незатухающих колебаний? Где они применяются?

18. Что такое вынужденные колебания? Запишите дифференциальное уравнение вынужденных колебаний.

19. От чего зависит амплитуда вынужденных колебаний? Запишите выражение для амплитуды и фазы при резонансе.

20. Что называется резонансом? Какова его роль?

2. Основы молекулярной физики и термодинамики

При изучении основ молекулярной физики и термодинамики следует уяснить следующее. Существует два способа описания процессов, происходящих в макроскопических телах (т.е. телах, состоящих из очень большого числа частиц - атомов или молекул), - статистический и термодинамический.

Статистическая (молекулярная) физика пользуется вероятностными методами и истолковывает свойства тел, непосредственно наблюдаемых на опыте (такие, как давление и температура), как суммарный, усредненный результат действия отдельных молекул. Молекулярно-кинетическая теория позволяет раскрыть глубинный смысл экспериментальных закономерностей, например, таких как уравнение Менделеева-Клапейрона. При решении задач на эту тему основное внимание уделено таким вопросам программы, как уравнение Менделеева-Клапейрона, закон Дальтона для смеси газов, уравнение молекулярно- кинетической теории (в контрольной работе это задачи.

Следует обратить внимание на статистические законы. Распределение молекул идеального газа по скоростям описывает распределение Максвелла, а в потенциальном поле энергии - распределение Больцмана. Зависимость давления от высоты для изотермической атмосферы описывается барометрической формулой.

При изучении явлений переноса, к которым относятся теплопроводность, диффузия и внутреннее трение, следует уяснить, что эти явления сходны между собой. В основе этого сходства лежит одинаковый молекулярный механизм перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.

Важно усвоить, что термодинамика, в отличие от молекулярной физики, не изучает конкретные взаимодействия, происходящие с отдельными атомами или молекулами, а рассматривает взаимопревращения и связь различных видов энергии, теплоты и работы.

При изучении основ термодинамики нужно четко усвоить такие понятия как термодинамическая система, термодинамический процесс, внутренняя энергия, энтропия и т.д. Задачи контрольной работы охватывают такие важные соотношения и понятия как первое начало термодинамики, внутренняя энергия, работа при различных изопроцессах.

Второе начало термодинамики формулируется как закон возрастания энтропии. Этот закон определяет направление протекания термодинамических процессов.

2.1. Основные формулы

Количество вещества[1] тела (системы)

где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему);

N_A – постоянная Авогадро (N_A = 6.02×10²³ моль^-1).

Молярная масса вещества

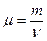где m – масса однородного тела (системы);

n – количество вещества этого тела.

Количество вещества смеси газов

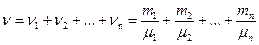где n_i, m_i, μ_i – соответственно количество вещества, масса, молярная масса i-го компонента смеси.

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

где m – масса газа;

μ – молярная масса газа;

R – универсальная газовая постоянная;

n – количество вещества;

T – термодинамическая температура.

Основные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T=const, m=const), PV=const,

или для двух состояний газа P₁V₁=P₂V₂;

б) закон Гей-Люссака (изобарный процесс: P=const; m=const), =const,

или для двух состояний ;

в) закон Шарля (изохорный процессе: V=const, m=const), 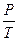=const,

или для двух состояний ;

г) объединенный газовый закон (m=const)

=const, или ,

где P₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии;

P₂, V₂, T₂ – те же величины в конечном состоянии.

Концентрация молекул

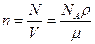где N – число молекул, содержащихся в данной системе;

r – плотность вещества;

V – объем системы.

Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение молекулярно-кинетической теории идеальных газов:

, или , или p=nkT,

где n – концентрация молекул;

k – постоянная Больцмана ( );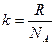

m_o – масса одной молекулы;

< _кв> – средняя квадратичная скорость молекул;

<W_к> – средняя кинетическая энергия поступательного движения молекулы газа.

Средняя кинетическая энергия молекулы газа:

где i - число степеней свободы молекулы. (i=i_пост+i_вращ)

Скорости молекул:

а) - средняя арифметическая;

б) 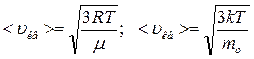- средняя квадратичная;

в) - наиболее вероятная,

где m_o – масса одной молекулы.

Среднее число соударений, испытываемых молекулой газа за 1 секунду:

где d – эффективный диаметр молекулы;

n – концентрация молекул;

< > – средняя арифметическая скорость молекул.

Средняя длина свободного пробега молекул газа

Закон диффузии (закон Фика):

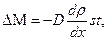
где – коэффициент диффузии.

Закон теплопроводности (закон Фурье):

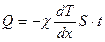Для идеального газа , - коэффициент теплопроводности,

где c_ν – удельная теплоемкость газа при постоянном объеме, r - плотность газа.

Закон Ньютона для внутреннего трения (вязкости):

где F – сила внутреннего трения между движущимися слоями газа (жидкости) площадью S;

– градиент скорости;

h – коэффициент внутреннего трения (динамическая вязкость).

Коэффициенты переноса связаны между собой соотношениями:

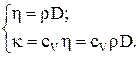
Молярные теплоемкости газа при постоянном объеме (C_V) и постоянном давлении (C_P):

, .

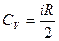Связь между удельной c и молярной C_n теплоемкостями

, ; , .

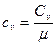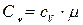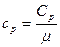Уравнение Майера для молярных теплоемкостей газа

C_P– C_V = R .

Внутренняя энергия идеального газа

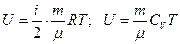где C_V – молярная теплоемкость газа при постоянном объеме.

Первое начало термодинамики

Q = DU + A,

где Q – количество теплоты, сообщенное системе (газу) или отданное ею;

DU – изменение внутренней энергии системы;

A – работа, совершенная системой против внешних сил.

Изменение внутренней энергии идеального газа:

Полная работа при изменении объема газа: ,

где V₁ и V₂ – соответственно начальный и конечный объемы газа.

Работа газа:

а) в изобарном процессе

, или ;

б) в изотермическом процессе

, или ;

в) в адиабатическом процессе

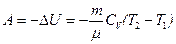, или ,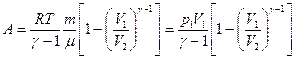

где T₁, T₂ и V₁, V₂ – соответственно начальные и конечные температуры и объемы газа;

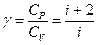– показатель адиабаты.

Уравнение адиабатического процесса (уравнение Пуассона):

P×V^γ=const; T×V^g-1=const; T^g×P^1-^g=const.

Термический КПД для кругового процесса (цикла)

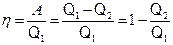где Q₁ – количество теплоты, полученное системой от нагревателя;

Q₂ – количество теплоты, отданное системой холодильнику;

A – работа, совершаемая за цикл.

Термический КПД цикла Карно

где T₁ – температура нагревателя;

T₂ – температура холодильника.

Изменение энтропии при равновесном переходе системы из состояния 1 в состояние 2:

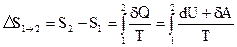2.2. Примеры решения задач к разделу «Молекулярная физика и термодинамика»

Пример № 1. 1 кг двухатомного газа находится под давлением р=8×10⁴ Па и имеет плотность 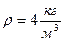. Найти энергию теплового движения молекул газа при этих условиях.

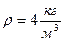
Дано: m = 1 кг i = 5 р=8×10⁴ Па	Решение: Внутренняя энергия газовой системы определяется уравнением U= 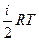(1), где i – количество ступеней свободы. Уравнение состояния идеального газа имеет вид: pV = RT.
U - ?

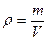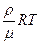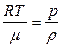Поскольку плотность , тогда p = но (2)

Таким образом из уравнений (1) и (2) имеем

U = 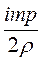. Подставив значения, получаем: U = = 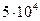Дж

Проверка размерности

Ответ: U = 5 × 10⁴ Дж.

Пример № 2. Чему равна наиболее вероятная скорость движения молекул кислорода при температуре Т = 273 К?

Дано: T = 273 K μ = 32 ∙10^-3 кг/моль	Решение: Наиболее вероятная скорость молекул определяется по формуле: 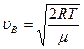, где R – газовая постоянная, μ – молярная масса.
_в – ?

Подставим численные значения:

Ответ:

Пример № 3. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27^оС и давлении 100 кПа.

Дано:

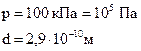
Решение: Средняя длина свободного пробега молекул вычисляется по формуле:

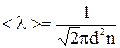(1), где d – эффективный диаметр молекулы, n – концентрация, т.е. число молекул в единице объема. Давление связано с концентрацией:

, где k – постоянная Больцмана.

<λ>, z - ?

Выразим n:

(2)

Подставим формулу (2) в (1) и получим:

(3)

Число соударений, происходящих между всеми молекулами за 1 с равно:

(4)

где N - число молекул в сосуде объемом V, < z > - среднее число соударений одной молекулы за 1 с.

Число молекул в сосуде равно:

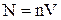(5)

Среднее число соударений молекулы за 1 с:

(6)

где < u > – средняя арифметическая скорость молекулы, равная

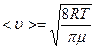(7)

Подставим в формулу (4) выражения (5), (6), (7):

Учтем формулу (2):

Проверим справедливость формулы по размерности величин

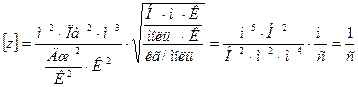
Подставим числовые значения:

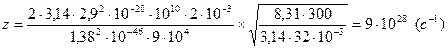
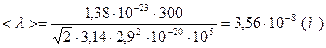
Ответ: , .

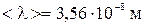Пример № 4. Горячая вода некоторой массы отдает теплоту холодной воде такой же массы и температуры их становятся одинаковыми. Показать, что энтропия при этом увеличивается.

Решение: Обозначим температуру горячей воды Т₁, холодной Т₂, а температуру смеси Q. Определим температуру смеси, исходя из уравнения теплового баланса:

где с – удельная теплоемкость, m – масса воды. Тогда: .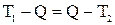

Отсюда температура смеси равна:

(1)

Изменение энтропии, происходящее при охлаждении горячей воды, равно:

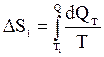Элементарное количество теплоты равно:

Тогда изменение энтропии, происходящее при охлаждении воды, равно:

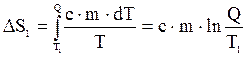Изменение энтропии, происходящее при нагревании холодной воды, равно:

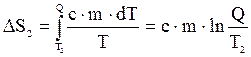Изменение энтропии системы равно:

С учетом (1) получим:

Так как , то 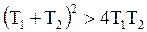, следовательно: и . Тогда 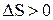, т.е. энтропия возрастает.

Ответ: энтропия возрастает.

2.3. Базовые задачи для самостоятельного решения

1. Найдите массу молекулы кислорода.

Ответ: m₀ = 5,32∙10^-26 кг.

2. Сколько молекул воздуха находится в комнате объемом 240 м³ при температуре 15 °С и давлении 750 мм рт. ст.?

Ответ: 6∙10²⁷.

3. Сколько молекул воздуха находится в 2 см³ воды?

Ответ: 6,7∙10²².

4. Какое количество вещества в молях составляют 5,418∙10²⁶ молекул?

Ответ: 900 моль.

5. По молярной массе определите массу молекулы водорода.

Ответ: 3,34∙10^{-27 кг.}

6. Сколько молекул содержится в 1 г кислорода?

Ответ: 1,8∙10²².

7. Сколько молекул содержится в капле воды диаметром 0,1мм?

Ответ: 1,82∙10¹⁶.

8. Какую массу имеют 2∙10²³ молекул азота?

Ответ: 9,3∙10^{-3 кг.}

9. Определите температуру газа, если средняя кинетическая энергия поступательного движения его молекул 4,14∙10^-21 Дж.

Ответ: 200 К.

10. Масса атома некоторого химического элемента равна 3,32∙10^{-25 кг. Найти массу одного моля этого химического элемента.}

Ответ: 0,2 кг/моль.

11. В сосуде находится 2 моля гелия. Сколько примерно атомов гелия в сосуде?

Ответ: 12∙10²³.

12. Какова средняя скорость движения свободного электрона при температуре -23 °С?

Ответ: м/c.

13. Сколько молекул воздуха находится в комнате объемом 240 м³ при температуре 15 °С и давлении 750 мм рт. ст.?

Ответ: N = 6∙10²⁷ молекул.

14. В баллоне емкостью 20 л находится кислород при температуре 17 °С и давлении 400 кПа. Спустя несколько часов температура кислорода возросла до 27 °С, а давление осталось прежним. Сколько кислорода вытекло?

Ответ: 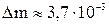кг.

15. Баллон содержит сжатый газ при 27 °С и давлении 20 атм. Каково будет давление, если из баллона будет выпущено 0,3 массы газа, а температура понизится до 12 °С?

Ответ: Р₂ = 13,3 атм.

16. До какой температуры нужно нагреть колбу, содержащую воздух при 20 °С, чтобы плотность воздуха уменьшилась в 1,5 раза?

Ответ: Т₂ = 1,5T₁; T₂ = 439,5 К.

17. Газ в некотором сосуде объемом 5 л при температуре 127 °С оказывает давление 2 атм. Какой объем займет этот газ при нормальных условиях?

Ответ: V_o = 5,46 ∙ 10^{-3 м3}.

18. Найти энергию W вращательного движения молекул, содержащихся в массе m = 1 кг азота при температуре t = 7° С.

Ответ: W = 8 Дж.

19. Найти удельную теплоемкость кислорода для условий нагревания: а) V = const ; б) р = const.

Ответ: с_v = 650 Дж/(кг∙К); с_p = 910 Дж/(кг∙К).

20. Найти отношение удельных теплоємкостей с_р/с_v для кислорода.

Ответ: .

21. Плотность некоторого двухатомного газа при нормальных условиях ρ = 1,43 кг/м³. Найти удельные теплоемкости с_v, и с_р этого газа.

Ответ: с_v = 648 Дж/(кг∙К); с_p = 509 Дж/(кг∙К).

22. Молярная масса некоторого газа µ = 0,03 кг/моль, отношение с_р / с_v = 1,4. Найти удельные теплоемкости с_v и с_р этого газа.

Ответ: с_v = 691 Дж/(кг∙К); с_p = 968 Дж/(кг∙К).

23. В закрытом сосуде находится масса m = 14 г азота под давлением р₁ = 0,1 МПа и температуре t = 27 °С. После нагревания давление в сосуде повысилось в 5 раз. До какой температуры t, был нагрет газ? Найти объем V сосуда и количество теплоты Q, сообщенное газу.

Ответ: Т = 1500 K; V = 12,5 л; Q = 12,4 кДж.

24. Какое количество теплоты Q надо сообщить массе m = 12г кислорода, чтобы нагреть его на Δt= 50° С при Р=const ?

Ответ: Q = 545 Дж.

25. Найти среднюю длину свободного пробега λ молекул углекислого газа при температуре t = 100 °С и давлении Р = 13,3 Па. Диаметр молекул углекислого газа d = 0,32 нм.

Ответ: λ = 859 мкм.

26. Найти среднее число столкновений z в единицу времени молекул углекислого газа при температуре t = 100 °С, если средняя длина свободного пробега λ = 870 мкм, а диаметр молекул 0,32 нм.

Ответ: z = 4,87∙10⁵c^-1.

27. Какое давление р надо создать внутри сферического сосуда, чтобы молекулы не сталкивались друг с другом, если диаметр сосуда: a) D = 1 см; б) D = 10 см; в) D = 100 см? Диаметр молекул газа d = 0,3 нм, температура в сосуде 300 К.

Ответ: а) Р=1,046 Па, б) Р=0,1046 Па, в) Р=0,0105 Па.

28. Найти коэффициент диффузии D водорода при нормальных условиях, если средняя длина свободного пробега λ = 0,16 мкм.

Ответ: D =9,06 ∙ 10^-5 м²/с.

29. При каком давлении р отношение вязкости некоторого газа к коэффициенту его диффузии 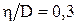кг/м³, а средняя квадратичная скорость его молекул = 632 м/с.

Ответ: м/с.

30. Найти диаметр d молекулы кислорода, если при температуре t = 0° С вязкость кислорода η = 18,8 мкПа·с.

Ответ: σ = 0,3 нм.

31. Найти коэффициент теплопроводности χ водорода, вязкость которого η = 8,6 мкПа∙с.

Ответ: χ = 89,33 мВт/(м∙К).

32. Углекислый газ и азот находятся при одинаковых температурах и давлениях. Найти для этих газов отношение: а) коэффициентов диффузии; б) вязкостей; в) теплопроводностей. Диаметры молекул газов считать одинаковыми.

Ответ: ; ; .

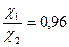33. Какое количество теплоты Q теряет помещение за время t = 1 час через окно за счет теплопроводности воздуха, заключенного между рамами? Площадь каждой рамы s = 4 м², расстояние между ними d = 30 см. Температура помещения t₁=180 °С, температура наружного воздуха t₂ = -20 °С. Диаметр молекул воздуха d = 0,3 нм. Температуру воздуха между рамами считать равной среднему арифметическому температур помещения и наружного воздуха. Давление P = 101,3 кПа.

Ответ: Q=24 кДж.

34. Масса m = 7 г углекислого газа была нагрета на ΔT = 10 К в условиях свободного расширения. Найти работу А расширения газа и изменение ΔW его внутренней энергии

Ответ: А=13,2 Дж; ΔW = 39,6 Дж.

35. Паровая машина мощностью Р=14,7 кВт потребляет за время t = 1 ч работы массу m = 8,1 кг угля с удельной теплотой сгорания q = 33 МДж/кг. Температура котла t = 200 °С, температура холодильника t₂ = 58 °С. Найти фактический к. п. д. η машины и сравнить его с к. п. д. идеальной тепловой машины, работающей по циклу Карно между теми же температурами.

Ответ: η=19,8%; ή=30%.

36. Идеальная холодильная машина, работающая по обратному циклу Карно, совершает за один цикл работу А=37кДж. При этом она берет тепло от тела с температурой t₂ = -10 °С и передает тепло телу с температурой t₁=17 °С. Найти к. п. д. η цикла, количество теплоты Q₂, отнятое у холодного тела за один цикл, и количество теплоты Q₁, переданное более горячему телу за один цикл.

Ответ: Q₁ = 397 кДж, Q₂=360 кДж.

37. Найти изменение ΔS энтропии при превращении массы m = 10 г льда (t = –20 °С) в пар (t_п = 100 °С). Удельная теплота плавления льда λ = 3,35·10⁵ Дж/кг, удельная теплоемкость воды c = 4200 Дж/(кг·К), удельная теплота парообразования воды – 2,26 МДж/кг.

Ответ: ΔS = 88 Дж/К.

38. Масса m = 6,6 г водорода расширяется изобарически от объема V₁, до объема V₂ = 2V₁. Найти изменение ΔS энтропии при этом расширении.

Ответ: ΔS = 66,3 Дж/К.

39. Найти изменение ΔS энтропии при плавлении массы m = 1кг льда (t = 0 °С), удельная теплота плавления льда с=0,33 МДж/кг.

Ответ: ΔS = 1209 Дж/К.

40. Найти изменение энтропии при переходе 8 г кислорода от объема 10 л при температуре 80°С к объему 40 л при температуре 300^оС.

Ответ: ΔS = 5,4 Дж/К.

2.4. Контрольные вопросы

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Механика жидкостей и газов	\|	Молекулярно-кинетическая теория идеальных газов

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.024 сек.