Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Про формулу І. Фішера

__________________________Довідкова інформація

Фішер (Ірвінг) Ірвін (1867─1947) ─ американський економіст і статистик. Навчався в Йельському університеті і там же в 1893─1935 рр. викладав політичну економію. Отримав визнання завдяки працям з економіко-математичного аналізу, теорії грошового обігу та кредиту, теорії індексів. Прибічник кількісної теорії грошей. У своїй моделі ринкової рівноваги визнавав неминучість криз але зводив їх до коливань кон’юнктури, які можна усунути змінюючи купівельну силу грошей та регулюючи їх кількість в обігу. Вважав, що абстрактна економічна теорія повинна базуватися на точному вимірі економічних процесів і явищ, підґрунтям яких є мотиви і поведінка підприємців.

В трактуванні І.Фішера класичний варіант кількісної теорії грошей характеризується рівнянням, яке у фінансах стали називати «рівнянням Фішера»: 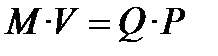, де М ─ кількість грошей в обороті; V─ швидкість обігу грошей за певний період; Р ─ середній рівень цін; Q ─ фізичний обсяг товарів і послуг, що реалізовані за цей період.

Але, крім «рівняння Фішера» в українських фінансах існують інші формалізовані вирази, що пов’язані у назві з його прізвищем.

В джерелі [4, стор. 231] читаємо: «Взаємозв’язок між номінальною ставкою процента та темпами інфляції одержало назву ефекту Фішера. Залежність визначається за таким рівнянням:

(10.36)

де: і ─ номінальна ставка процента (банківська); r ─ реальна ставка процента (купівельна спроможність); Т ─ темп інфляції».

В іншому джерелі [3, стор. 106] така інформація: «…розрізняють … реальну та номінальну процентні ставки. Остання є номінально встановленим банківським процентом (і). Ця величина, скоригована на темп інфляції ( 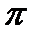), становить реальну процентну ставку ( ):

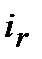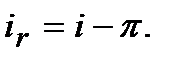(10.37)

Рівняння (10.37), записане у формі 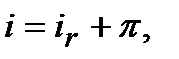має назву рівняння Фішера…».

Досить поширеною є така розрахункова конструкція [9, стор. 83-84]. «Задамо річний темп інфляції 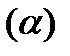і просту річну ставку позичкового процента (і). Тоді для нарощеної суми 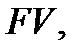що перетворюється в умовах інфляції в суму 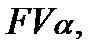можна використовувати формулу:»

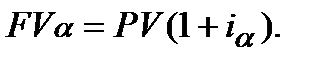
Для даної суми … можна записати ще одне співвідношення:

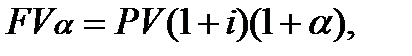
а потім скласти рівняння еквівалентності, дорівнявши множники нарощення, на підставі того, що 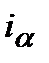─ процентна ставка, що враховує інфляцію:

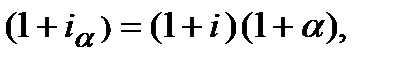
з якого випливає, що:

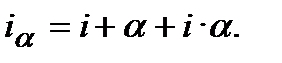(10.38)

Це відома формула І.Фішера. У ній сума є величиною, яку потрібно додати до реальної ставки прибутковості для компенсації інфляційних втрат, і називається інфляційною премією».

В наведеній Довідковій інформації формули (10.36), (10.37), (10.38) мають різні назви: «ефект Фішера», «рівнянням Фішера», «формула І.Фішера». Може ці формули описують різні розрахунки? Ні, ці формули про одне і теж: про співвідношення процентних ставок при врахуванні інфляції. Може вихідні умови, за яких працюють ці формули, відрізняються? Також ні. В цих формулах процентні ставки ─ річні, показники, позначені різними позначками ( Т, 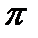, ) ─ це показники темпу інфляції і вони, також, річні. Строк, в межах якого функціонують ці формули, ─ рік.

На наш погляд, це приклад термінологічної неузгодженості у вітчизняній учбовій, а від того, можливо, і в науковій літературі. Цілком доречно, на наш погляд, застосовувати термін «рівняння Фішера» до рівняння 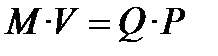, а до формул (10.36), (10.37), (10.38) вираз ─ «формула Фішера».

В контексті формул (10.36), (10.37), (10.38) є три особливості, на першу з яких майже у всіх навчальних джерелах загострюють увагу, а на другу і третю ще ніхто не звертав уваги.

Перша особливість. Порівнюючи формулу (10.38) з формулами (10.36) та (10.37) бачимо, що формули (10.36) та (10.37) «не беруть до уваги» складову, яка є у формулі (10.38), а саме ─ доданок 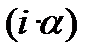. В формулах (10.36) та (10.37) для розрахунку процентної ставки, що враховує інфляцію, до величини процентної ставки без врахування інфляції додають величину рівня інфляції. Це може привести до грубих помилок. Щоб показати, що формулами (10.36) та (10.37) можна користуватися, додають умову, що доданок практично не впливає на розрахунок при 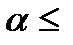6%. Отже, формули (10.36) та (10.37) дають прийнятний результат при наступних умовах: строк фінансової операції ─ рік; ставки ─ річні; темп інфляції ─ річний та не перевищує 6%; та і номінальна (банківська) ставка, за логікою розрахунку, теж не повинна бути великою. Формули (10.36), (10.37) мають дуже обмежене поле застосування. На цій підставі посилатися на них як на приклад чисельного врахування інфляції у фінансових розрахунках, не є достатньо коректним.

Друга особливість стосується формули (10.38). На практиці, як це не парадоксально, формули у запису (10.38) не існує. Запис у вигляді (10.38): 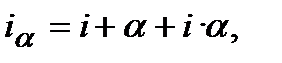─ це макет формули, це ─ кліше, яке дуже нагадує формулу. В практичних розрахунках використовують не одну, як помилково вважають, а дві формули, яки записом нагадують (10.38). Як вже наголошувалось, запис (10.38) виник з рівняння еквівалентностіза умов: строк фінансової операції ─ рік; ставки ─ річні; темп інфляції ─ річний. При застосуванні цих умов до формули (10.23) маємо:

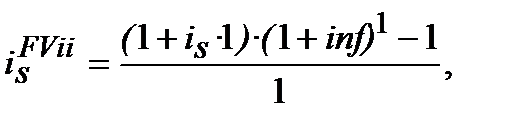
де 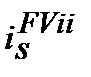─ проста процентна еквівалентна ставка (еквівалентна простій 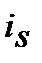та inf) для розрахунку майбутньої вартості з урахуванням компенсації інфляційного зростання цін. Перетворюючи далі попереднє рівняння одержуємо:

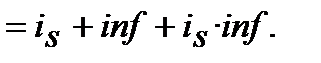(10.39)

Таку ж формулу одержуємо і про застосуванні «річних умов» до формули (10.27)

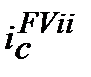
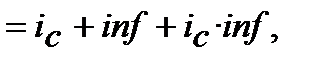(10.40)

де 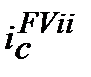─ складна процентна еквівалентна ставка (еквівалентна складній 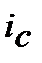та inf) для розрахунку майбутньої вартості з урахуванням компенсації інфляційного зростання цін. Іншими словами 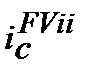─ це складна процентна брутто-ставка.

Можемо зробити висновок, що для формул (10.39) та (10.40) за «річних умов» механізм нарахування процентів, ─ простий, чи складний, ─ не має значення, тобто, формули (10.39) та (10.40) ідентичні. Також, наголошуємо, що формули (10.39) та (10.40) дають розрахунок з урахуванням компенсації інфляційного зростання цін. Якщо застосувати позначки процентних ставок інші, наприклад: 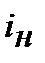─ номінальна процентна ставка; 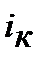─ процентна ставка з урахуванням компенсації інфляції (брутто-ставка), 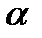─ темп інфляції, то формули (10.39) та (10.40) набувають вигляду:

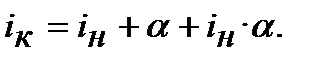(10.41)

Якщо застосувати рівняння еквівалентностіза умов: строк фінансової операції ─ рік; ставки ─ річні; темп інфляції ─ річний до формул реального знецінення грошей внаслідок інфляції ─ до формул (10.24) і (10.28) та позначити реальну ставку через 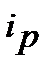то перетворені відносно 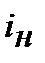формули (10.24) та (10.28) мають такий вигляд:

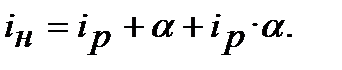(10.42)

Як бачимо, формули (10.41) та (10.42) в запису нагадують формулу (10.38), але, тільки нагадують і тільки у формі запису. Формули (10.41) та (10.42) різняться. Формула (10.41) ─ це формула взаємозв’язку номінальної ставки 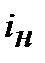зі ставкою повної компенсації інфляційного зростання цін 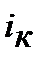, а формула (10.42) ─ це формула взаємозв’язку тієї ж номінальної процентної ставки 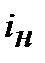з реальною ставкою 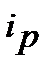. Цікавим є те, що у підручниках, як правило, надається одна з формул, або (10.41), або (10.42), але автори надають її у запису (10.38) і тому, не помічають, що формул Фішера з використанням процентних ставок ─ дві. Наприклад: Н.І. Машина у посібнику [9, стор. 84] виводить формулу з урахуванням «компенсації інфляційних утрат» ─ 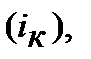тобто формулу (10.41), але номінальну ставку 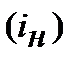іменує реальною ставкою а це вже показник із формули (10.42).

Не має значення чи були такі формули, мається на увазі формули (10.41) та (10.42), в теоретичних викладках Ірвіна Фішера, головне, що такі формули існують, працюють в практичних розрахунках і пропоную називати їх і надалі формулами Фішера.

Третя особливість─ показник інфляційної премії. Показників інфляційної премії ─ також два, відповідно до формул (10.41) та (10.42) :

─ ─ інфляційна премія що збільшує номінальну ставку і, як результат, ─ є інфляційною премією, що компенсує інфляційні втрати, отже, загалом ─ компенсаційна інфляційна премія;

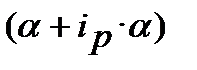─ ─ інфляційна «премія», що характеризує розмір інфляційних втрат в межах нарощення за номіналь-ною ставкою, з іншої сторони це ─ інфляційна премія, що збільшує реальну ставку до розміру номінальної ставки. По суті, цей показник не коректно іменувати «інфляційна премія», більш придатним є термін «інфляційна втрата», «інфляційна знижка», «інфляційне знецінення». Узагальнена назва може бути такою ─ реальна інфляційна втрата, або ─ реальне інфляційне знецінення.

І в завершення підрозділу 10.4 ще раз не завадить нагадати, ─ формули Фішера характеризують вплив інфляції та застосовуються тільки в межах «річних умов», а саме: строк фінансової операції ─ рік; ставки ─ річні; темп інфляції ─ показник за рік.

_Приклад 10.4_________________________________

Читайте також:

Сутність класичної кількісної теорії грошей та роль І. Фішера в її розвитку. Варіанти кількісної теорії грошей.

<== попередня сторінка	\|	наступна сторінка ==>
Задача 3.	\|	Задача 1.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.