Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

При додатковому їх поповненні

Розглянемо модель цієї задачі на прикладі визначення оптимальної кількості автомобілів транспортної фірми при випадковій кількості резервних автомобілів і випадковому їх попиті. За критерій оптимальності приймемо математичне сподівання прибутку підприємства. Припустимо, що експлуатація одного автомобіля в одиницю часу характеризується такими показниками:

прибуток від експлуатації одного автомобіля;

витрати на утримання одного автомобіля, який належить автопід-приємству;

збитки від простою одного автомобіля, який належить підприємству;

витрати на використання орендованого автомобіля;

Е – можливі втрати прибутку, пов’язані з недостачею автомобілів при наявності попиту.

Показники Р, B, C, D можуть бути розраховані за відповідними методиками. Величина Е має гіпотетичний характер і у залежності від конкретного змісту задачі може варіюватись у значних межах.

Введемо позначення:

n – кількість власних автомобілів на підприємстві;

X – дискретна випадкова величина, яка характеризує попит на транспортні послуги, виражений у необхідній кількості автомобілів;

Y – дискретна випадкова величина, яка характеризує пропозицію додаткових автомобілів, які може мати підприємство (власних неспеціалізованих автомобілів або орендованих).

Для розв’язання задачі необхідно знати закони розподілу ймовірностей випадкових величин X і Y. Позначимо через 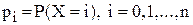імовірність попиту на i автомобілів, а через 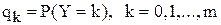імовірність пропозиції k автомобілів. Величини (i, p_i) характеризують закон розподілу ймовірностей попиту на автомобілі, (k, q_k) – розподіл імовірностей пропозиції додаткових автомобілів. Ці розподіли можуть визначатись у вигляді дискретних рядів розподілу за статистичними даними, або у вигляді розподілу Пуассона, який теж визначається за статистичними даними.

Припустимо, що підприємство має у своєму розпорядженні n основних автомобілів. Тоді множину значень Х і Y можна розбити на три області:

Ø попит на автомобілі Х менше ніж кількість основних автомобілів і має місце втрата прибутку від невикористання автомобілів;

Ø попит на автомобілі Х перевищує кількість основних автомобілів але є достатня кількість пропозицій додаткових автомобілів і підприємство має можливість одержати певний прибуток від їх використання;

Ø кількість основних і додаткових автомобілів n i Y недостатня для задоволення попиту 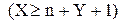і має місце втрачений прибуток від нестачі автомобілів.

Визначимо середній валовий прибуток підприємства в одиницю часу, який є різницею між прибутком за рахунок реалізації послуг та витратами з урахуванням можливої втрати прибутку від нестачі автомобілів. Він дорівнює математичному сподіванню функції f(n,X,Y), аргументами якої є детермінована величина n і випадкові величини X i Y

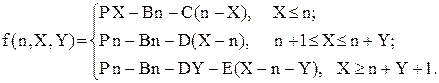(3.48)

Усереднюючи цей вираз по розподілам ймовірностей величин X і Y, одержимо математичне сподівання функції f(n,X,Y)

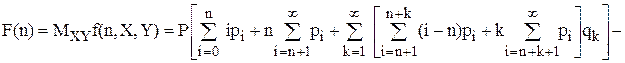
При фіксованих значеннях n функція F(n) є опуклою уверх по n і має єдиний максимум. Задача формулюється так: знайти значення 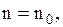при якому функція прибутку F(n) приймає максимальне значення

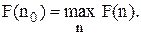(3.50)

Оскільки F(n) є функція дискретного аргументу, то для знаходження її екстремуму не можна застосувати класичний метод, прирівнюючи до нуля її похідну. Тому знаходження екстремуму здійснюється за перебірним алгоритмом, послідовно обчислюючи значення F(n) для 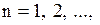доки не буде знайдена точка екстремуму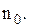

Приклад 3.16. Проектується транспортна фірма, яка в залежності від попиту на перевезення повинна мати певну кількість автомобілів, яка б забезпечила одержання максимального прибутку. Припустимо, що показники прибутку і витрат на один автомобіль мають такі значення: Р=1500, B=200, C=150, D=1000, E=800 доларів.

Попит на транспортні послуги за період t, виражений у необхідній кількості автомобілів, розподілений за законом Пуассона з параметром λ. Припускається, що у разі нестачі спеціалізованих автомобілів, фірма може тимчасово залучати деяку додаткову кількість автомобілів інших підприємств. Пропозиція додаткових автомобілів (власних або орендованих) також розподілена за законом Пуассона з параметром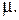

Виходячи з економічних інтересів фірми, треба визначити оптимальну кількість автомобілів, яка б забезпечила максимальний прибуток.

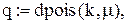
Оскільки розподіли ймовірностей попиту і пропозиції автомобілів задані у вигляді розподілів Пуассона, які залежать від параметрів λ і μ відповідно, то спочатку визначаємо ці параметри. Визначення параметрів здійснюється на основі статистичних даних за відомою методикою. Далі одержуємо ряди розподілів попиту і пропозиції. Ці розподіли у Mathcad визначаються функцією dpois() у вигляді: де 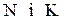верхні границі індексів та У результаті чого одержуємо ряди (вектори) розподілу попиту , і пропозиції додаткових автомобілів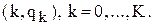

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Алгоритм реалізації моделі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.