
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тапсырмалар.
№1-есеп.
Балаларда қызылиектің экссудатациясының жылдамдығы (мл/тәулік):
| Қалып | 0,75 | 0,82 | 0,73 | 0,86 | 0,85 | 0,81 | 0,8 | 0,78 | 0,79 | 0,82 |
| Гингивит | 1,8 | 1,4 | 1,32 | 1,49 | 1,52 | 1,5 | 1,7 |
Таңдама таралу түрі қалыпты деп есептеп, екі көрсеткіштін орта мәндері арасындағы айырмашылықтың статистикалық мәнділігін анықтаңдар.
№2-есеп.
Кальций антагонистер тобына жататын нифедипин препаратының қан тамырларын кеңейтетін қасиеті бар, және оны жүректің ишемиялық ауруын емдеу кезінде қолданады.Нифедипин және плацебоны қабылдағаннан кейін коронарлы артерияның диаметрін өлшеген және төмендегідей деректердің екі таңдамасы алынған ( мм):
| Плацебо: | 2,5 | 2,2 | 2,6 | 2,0 | 2,1 | 1,8 | 2,4 | 2,3 | 2,7 | 2,7 | 1,9 |
| Нифедипин: | 2,5 | 1,7 | 1,5 | 2,5 | 1,4 | 1,9 | 2,3 | 2,0 | 2,6 | 2,3 | 2,2 |
Келтірілген деректер бойынша нифедипин коронарлық артерияның диаметріне ықпал етеді деп айтуға бола ма?
№3-есеп.
Балаларда ынтасыз сілекей бөліну жылдамдығы (мл/мин.):
| Операцияға дейін | 0,18 | 0,19 | 0,14 | 0,22 | 0,15 | 0,17 |
| Уранопластикадан кейін | 0,2 | 0,22 | 0,16 | 0,26 | 0,15 | 0,18 |
Таңдама таралу түрі қалыпты деп есептеп, екі көрсеткіштін орта мәндері арасындағы айырмашылықтың статистикалық мәнділігін анықтаңдар.
№4-есеп.
Манн-Уитни критерийі көмегімен тәуелсіз таңдамалар бір бас жиынтықтан алынғандығы туралы жорамалды тексерейік.
Дәрмек затының қандағы мөлшері, ммоль/г
| 1 топ | ||||||||||
| 2 топ |
Есеп.
Қышқылдың әсерінен кейін эмаль қабатың микроқабаттылығы (Со ОЭДФ):
| Әсерге дейін | 0,16 | 0,129 | 0,135 | 0,15 | 0,125 | 0,13 |
| Әсерден кейін | 0,195 | 0,178 | 0,166 | 0,16 | 0,11 | 0,12 |
Таңдама таралу түрі қалыпты емес деп есептеп, екі топ арасындағы айырмашылықтың статистикалық мәнділігін анықтаңдар.
№6-есеп.
Дальтонизм белгісі бойынша 1000 адам іріктелді. Төменде көрсетілген мәліметтер бойынша дальтонизм белгісі мен жыныс арасындағы тәуелділікті зерттеу, α = 0,05 кезінде.
| Ерлер | Әйелдер | |
| дальтониктер | ||
| дальтониктер емес |
№7-есеп.
Аңдаусыз бала өлімі синдромы – жасы 1 аптадан 1 жылға дейінгі балаларөлімінің негізгі себебі. Әдетте өлім баланың сап-сау кезінде, ұйқыда жатқанда болады, сондықтан қауіп-қатер факторларын анықтау өте маңызды. Аңдаусыз бала өлімі синдромы жетілмей туылған балаларда, негрлерде және табысы нашар отбасыларда жиі кездеседі деп саналады. Алайда, зерттеушілер осы деректердің растығын анықтап білу мақсатында 1960 жылдан бастап 1967 жылға дейін Калифорния штатындағы Окленда перзентханаларының бірінде дүниеге келген 19047 бала жөнінде деректер жинады. Балаларды 1 жасқа дейін бақылады. Аңдаусыз бала өлімі синдромынан 44 сәби өлді. Синдроммен байланысты белгілерді табыңыз.
| Фактор | Аңдаусыз бала өлімі синдромы | ||
| Бар | Жоқ | ||
| Нәсіл | Ақтар | ||
| Негрлер | |||
| Басқалар |
Колмогоров- Смирновтың келісім критерийі
Это наиболее мощный критерий из серии непараметрических критериев, применяемых при сопоставлении двух различных групп наблюдений.
Деректерді өңдеу реті:
1. Бақылаудың салыстырылатын топтарында кездесетін варианталардың барлығы бір қатарға өсу ретімен біріктіріледі.
2. Бірінші және екінші топтар үшін варианталардың жиіліктері жазылады.
3. Жиіліктер жинақталған тәртіппен қойылады.
4. Жинақталған жиіліктер сәйкес топтардағы бақылаулар санына бөлінеді.
5. Топтар бойынша жинақталған жиіліктердің айырымы есептеледі және бұл кезде таңба есепке алынбайды.
6. D ең жоғарғы айырма табылады.
7. l2 критерийі есептеледі: 
8. l2 алынған мәні мен шекаралық мәндері салыстырылады, олар 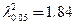
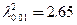
9. Егер  , онда салыстырылатын топтар арасындағы айырмашылық маңызды.
, онда салыстырылатын топтар арасындағы айырмашылық маңызды.
ЗАДАЧА
Условие задачи: Были изучены сроки гибели животных (в минутах) после введения токсического вещества. Ряд Х — контрольная группа, в которой лечение не проводилось; ряд Y — опытная группа, ниже проводилось определенное лечение.
| Х | n=7 | ||||||||
| У | n=8 |
Задание: определить, существенны ли различия в сроках гибели животных.
Н0: эмпирикалық таралу мен теориялық таралу дың арасында ешқандай айырмашылық жоқ, различия в сроках гибели животных не существенны.
Н1: эмпирикалық таралу мен теориялық таралу дың арасында ешқандай айырмашылық бар, различия в сроках гибели животных существенны.
α=0,05
| Варианты Х и У в последовательно возрастающем порядке | Частоты вариант по группам | Накопленные частоты по группам | 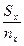
| 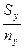
| Разности
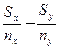
| ||

| 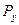
| 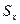
| 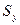
| без учета знаков | |||
| - | 0,14 | 0,14 | |||||
| - | 0,14 | 0,125 | 0,015 | ||||
| - | 0,43 | 0,125 | 0,305 | ||||
| 0,57 | 0,25 | 0,32 | |||||
| - | 0,57 | 0,37 | 0,2 | ||||
| - | 0,71 | 0,37 | 0,34 | ||||
| - | 0,86 | 0,37 | 0,49 | ||||
| - | 0,86 | 0,62 | 0,24 | ||||
| - | 0,62 | 0,38 | |||||
| - | 0,75 | 0,25 | |||||
| - | 0,88 | 0,12 | |||||
| - | |||||||
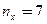 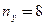
|
D (максимальная разность) равняется 0,49.
По формуле рассчитывается 
так как 0,888 < 1,84, то λ2< λ 20,05
Следовательно, еще раз подтверждается вывод о том, что сроки гибели животных в опытной и контрольной группах существенно не отличаются друг от друга и различия, которые имеют место, случайны.
Тапсырма: Футболшылардың ойын деңгейін анықтау үшін 2 айлық және 3 жылдық футболшылардың тобының нәтижесі алынды. 2 айлық және 3 жылдық футболшылардың тобының ойынында айырмашылық бар ма?
| Ойын үйрену деңгейі | 2-айлық ойыншылар тобы | 3-жылдық ойыншылар тобы |
| Өте жақсы | ||
| Жақсы | ||
| Орташа | ||
| Төмен |
Дисперсиялық талдау
Дисперсиялық талдау – бұл екіден артық топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын талдау әдісі.
Орта мәндердің арасындағы айырмашылықтарды анықтау үшін дисперсиялар қолданылады.
Дисперсиялық талдау деп таңдама дисперсиялардысалыстыру арқылы екі немесе бірнеше таңдамаларды зерттеуге арналған статистикалық әдістер тобын айтады.
Дисперсиялық талдау міндеттері:
ü белгіленген немесе кездейсоқ болулары мүмкін бірнеше деңгейлермен сипатталатын факторлардың ықпалын зерттеу.
ü Мысалы,А факторы – үш деңгейден тұратын аурудың ауырлығы: жеңіл, орта, ауыр.
Дисперсиялық талдаудың негізгі идеясы:
Таңдама дисперсияны екі компенентке бөлу:
ü Факторлық дисперсия,
ü Қалдық дисперсия.
Жалпы ортаға қарасты, топтардың орта мәндерінің шашырауын сипаттайтын факторлық дисперсияны топаралық дисперсия деп атайды.
Топтардың түзетілген таңдама дисперсиялары үшін орта арифметикалық мән болып табылатын қалдық дисперсияны топішілік дисперсия деп атайды.
Бірфакторлық дисперсиялық талдау
Айталық, қандай да бір А факторының қандай да бір қалыпты таралған Х шамасының қалыптасуына ықпалын зерттеу керек болсын.
А факторы k деңгейлі: А1,А2,...,Аk..
| Сыныулар номері | Фактор денгейі | |||
| A1 | A2 | … | Ak | |
| x11 | x12 | … | x1k | |
| x21 | x22 | … | x2k | |
| ... | … | … | ||
| nj | 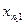
| 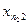
| … | 
|
| Топталган орта мән | 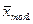
| 
| … | 
|
| Жалпы орта мән | 
|
Бірфакторлы дисперсиялық талдау негізіне топаралық және қалдық дисперсияны салыстыру жатады.
Өлшеніп отырған шамаларға әсер етуші фактор, бас топаралық дисперсия бас қалдық дисперсиядан үлкен болса ғана орта мәнге маңызды ықпал етеді.
Фактордың әр деңгейі бойынша элементтердің таңдама топтық орта мәндері:
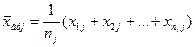
Ауытқулардың квадраттарының жалпы қосындысы:
 немесе
немесе  , мұндағы
, мұндағы 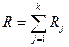 ,
, 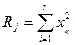
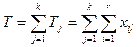
Ауытқулардың квадраттарының факторлық қосындысы:
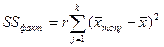 немесе
немесе 
Ауытқулардың квадраттарының қалдық қосындысы:
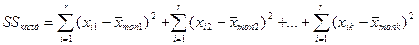 мәндердің шашырау дәрежесін сипаттайды.
мәндердің шашырау дәрежесін сипаттайды.
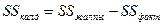
 - жалпы дисперсия
- жалпы дисперсия
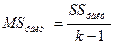 - факторлық дисперсия
- факторлық дисперсия
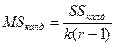 -қалдық дисперсия
-қалдық дисперсия
Дисперсиялық талдауды жүргізу әдісі:
1. Нөлдік және балама жорамалдарды құрамыз:
Н0: топтық бас орта мәндер тең, және таңдама орталар арасындағы айырмашылықтар кездейсоқ, фактор оларға ықпал етпейді.
H1: таңдама орталар арасындағы айырмашылықтар кездейсоқ емес және оларға фактор ықпал етеді.
2. α мәнділік деңгейі беріледі ( мысалы, α=0,05 немесе α=0,01).
3. Есептеледі MSфакт және MSкалд
Егер  , онда нөлдік жорамал қабылданады.
, онда нөлдік жорамал қабылданады.
Егер 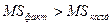 , онда
, онда 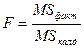 Фишер статистикасы есептеледі.
Фишер статистикасы есептеледі.
4. Fтәж есептегеннен кейін, Fсыни кесте бойынша Фишер таралуының сыни мәндерін табады. Ол k-1 және k(r-1) еркіндік дәрежелерінің сандарына сәйкес келуі керек.
5. Fтәж және Fсыни салыстырылады.
Егер Fтәж < Fсыни , онда берілген мәнділік деңгейінде Н 0 нөлдік жорамалы қабылданады және фактор орта мәнге ықпал етпейді деген қорытынды жасалынады.
Егер Fтәж > Fсыни, онда нөлдік жорамал жоққа шығарылады және фактор ықпалы маңызды деп танылады.
Дисперсиялық талдау кестесі:
| Вариациялар, дисперсиялар | Квадраттарының қосындысы (ауытқулар) | Еркіндік дәрежелерінің саны | Орта квадрат MS | 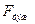
| 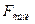
|
| Топаралық (фактор А) | 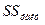
| k-1 | 
| 
| 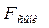
|
| Топішілік (қалдық) | 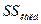
| k(r-1) | 
| ||
| Жалпы | 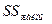
| kr-1 | 
|
Мысал: Темекі шегудің тыныс алу жолдары ауруларына ықпалы.
Белгілі бір жас шамасы категориясындағы үлкейген тұрғындар арасында екі жыл ішінде тыныс алу жолдары ауруына ұшыраған адамдардың саны белгіленді. Зерттеу мақсаты темекі шегудің тыныс алу мүшелері ауруларына ықпалын статистикалық дәлелдеу. Әрқайсысы 4 адамнан тұратын 3 топ кездейсоқ таңдалынып алынды, олардың: І топ-темекі шекпейтіндер; ІІ- темекі шегу стажы 5 жылға дейін, ІІІ- темекі шегу стажы 5 жылдан көп.
Зерттелетін фактор А: темекі шегу.
Фактор деңгейлері: А1 А2 А3 – темекі шегу стажы.
Темекі шегу факторына жауап – тыныс алу жолдары ауруларының саны.
| Сыныулар номері | Фактор денгейі | ||
| A1 | A2 | A3 | |
1. Жорамалдарды ұйғарамыз:
H0- темекі шегу тыныс алу мүшелері ауруларына ықпал етпейді.
H1 - темекі шегу тыныс алу мүшелері ауруларына маңызды ықпал етеді.
k=3 r=4 n=12
| 1 әдіс | 2 әдіс |
T1=1+0+1+2=4
T2=3+2+2+1=8
T3=3+4+5+3=15
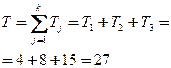
 R1=12+02+12+22=6
R2=32+22+22+12=18
R3=32+42+52+32=59
R=6+18+59=83
Онда
R1=12+02+12+22=6
R2=32+22+22+12=18
R3=32+42+52+32=59
R=6+18+59=83
Онда  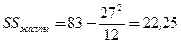  
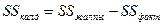 
| 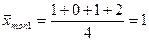
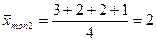
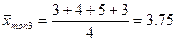
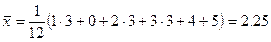

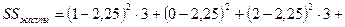
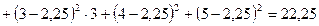
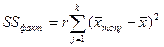 
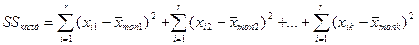 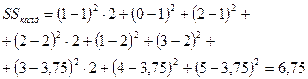
|
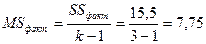
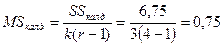
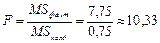 ,
, 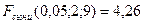
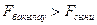 , яғни нольдік болжам жоққа шығарылады.
, яғни нольдік болжам жоққа шығарылады.
Қорытынды: темекі шегу тыныс алу мүшелері ауруларына маңызды ықпал етеді.
| Вариациялар, дисперсиялар | Квадратта-рының қосындысы (ауытқулар) | Еркіндік дәрежелерінің саны | Орта квадрат MS | 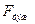
| 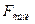
|
| Топаралық (фактор А) | 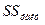 =15,5 =15,5
| k-1=2 |  =7,75 =7,75
|  
| 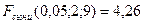 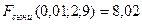
|
| Топішілік (қалдық) | 
| k(r-1)= 9 |  =0,75 =0,75
| ||
| Жалпы | 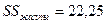
| к(r-1)=11 | 
|
Тапсырма. Бірфакторлы дисперсиялық талдау жасау. Зерттелетін фактор әсерінің күшін бағалау. Қорытындылар жасау.
1 Есеп. Диурездің тәулік уақытына байланысты өзгерісі (Зимницкий сынамасы):
| № | Несеп жинау уақыты (сағ) | |||||||
Регрессиялық талдау.
Айталық, бізде  және
және  екі параметрдің n мәндер жұбы
екі параметрдің n мәндер жұбы  бар болсын. Яғни, бір ғана объектінің екі параметрі өлшенген. Осы параметрлердің арасында қандай да бір мәнді байланыс бар ма деген сұраққа жауап беру керек.
бар болсын. Яғни, бір ғана объектінің екі параметрі өлшенген. Осы параметрлердің арасында қандай да бір мәнді байланыс бар ма деген сұраққа жауап беру керек.
 және
және  кездейсоқ шамалары өзара тәуелді немесе тәуелсіз болуы мүмкін. Тәуелділіктің екі түрі бар: функционалдықжәне статистикалық. Математикада
кездейсоқ шамалары өзара тәуелді немесе тәуелсіз болуы мүмкін. Тәуелділіктің екі түрі бар: функционалдықжәне статистикалық. Математикада  айнымалысының
айнымалысының  айнымалысынан функционалдық тәуелділігідеп
айнымалысынан функционалдық тәуелділігідеп  - тің әрбір мүмкін мәніне қандай бір белгілі ереже бойынша
- тің әрбір мүмкін мәніне қандай бір белгілі ереже бойынша  - тің бір ғана мүмкін мәні сәйкес қойылатын
- тің бір ғана мүмкін мәні сәйкес қойылатын  түріндегі тәуелділікті айтады.
түріндегі тәуелділікті айтады.
Алайда, егер  және
және  кездейсоқ шамалар болса, онда олардың арасында статистикалықдеп аталатын тәуелділіктің басқа түрі болуы мүмкін.
кездейсоқ шамалар болса, онда олардың арасында статистикалықдеп аталатын тәуелділіктің басқа түрі болуы мүмкін.  және
және  кездейсоқ шамаларының мәндерінің қалыптасуына әртүрлі факторлар әсер етеді. Осы факторлардың әсер етуі нәтижесінде
кездейсоқ шамаларының мәндерінің қалыптасуына әртүрлі факторлар әсер етеді. Осы факторлардың әсер етуі нәтижесінде  және
және  нақты мәндері қалыптасады. Айталық,
нақты мәндері қалыптасады. Айталық,  және
және  - ке бірдей факторлар, мысалы
- ке бірдей факторлар, мысалы  әсер етсін, онда
әсер етсін, онда  және
және  бір-бірімен толық сәйкестікте болады және функционалды байланысады. Енді айталық, Х – ке
бір-бірімен толық сәйкестікте болады және функционалды байланысады. Енді айталық, Х – ке  , ал
, ал  -ке тек қана
-ке тек қана  және
және  факторлары әсер ететін болсын.
факторлары әсер ететін болсын.  және
және  екеуі де кездейсоқ шамалар, бірақ олардың екеуіне бірдей әсер ететін
екеуі де кездейсоқ шамалар, бірақ олардың екеуіне бірдей әсер ететін  және
және  ортақ факторлары бар болғандықтан, олар өзара байланысты және бұл байланыс функционалдыбола алмайды, себебі: кездейсоқ шамалардың біреуіне ғана әсер ететін
ортақ факторлары бар болғандықтан, олар өзара байланысты және бұл байланыс функционалдыбола алмайды, себебі: кездейсоқ шамалардың біреуіне ғана әсер ететін 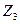 факторы
факторы  және
және  мәндерінің арасындағы тікелей (функционалдық) тәуелділікті бұзады. Бұл жағдайдағы байланыс сынаудан сынауға дейін өзгеріп отыратын кездейсоқ байланыс. Мұндай байланысты статистикалықдеп атайды. Бұл жағдайда
мәндерінің арасындағы тікелей (функционалдық) тәуелділікті бұзады. Бұл жағдайдағы байланыс сынаудан сынауға дейін өзгеріп отыратын кездейсоқ байланыс. Мұндай байланысты статистикалықдеп атайды. Бұл жағдайда  - тің әрбір мәніне функционалдық тәуелділіктегі сияқты
- тің әрбір мәніне функционалдық тәуелділіктегі сияқты  - тің бір ғана мәні емес, қандай да бір мәндер жиыны сәйкес келуі мүмкін.
- тің бір ғана мәні емес, қандай да бір мәндер жиыны сәйкес келуі мүмкін.
Анықтама 1.Егер бір кездейсоқ шаманың өзгеруіне екінші кездейсоқ шаманың таралу заңының өзгеруі сәйкес келсе, онда олардың арасындағы тәуелділік статистикалықдеп аталады.
Анықтама 2. Егер бір кездейсоқ шаманың өзгеруіне екінші кездейсоқ шаманың орта мәнінің өзгеруі сәйкес келсе, онда олардың арасындағы статистикалық тәуелділік корреляциялықдеп аталады.
Корреляциялық тәуелділікпен байланысқан кездейсоқ шамаларды корреляцияланғандеп атайды.
Корреляциялық тәуелділіктің мысалдары: дененің салмағымен бойдың ұзындығының арасындағы тәуелділік: бойдың ұзындығының (Х) әрбір мәніне дене салмағының (  ) мәндер жиыны сәйкес келеді.
) мәндер жиыны сәйкес келеді.
- сыртқы факторлардың әсері мен аурудың арасындағы тәуелділік, мысалы, ауаның шаң – тозаңдығы, радиация деңгейі, күн көзінің өтімділігіжәне т. б.;
- аңдардың салмағы мен олардың қандарындағы гемоглобиннің мөлшері арасындағы тәуелділік;
- объектіге егілген препараттың мөлшерімен оның қандағы ерітіндісінің арасындағы тәуелділік;
Сол сияқты корреляция
- ионданған сәуле шығару дозасы мен мутация санының арасында;
- адам шашының пигменті мен көзінің түсі арасында;
- студенттердің жіберген дәрістері мен емтихандағы бағаларының
арасында бар.
Табиғатта ең жиі кездесетін тәуелділік – ол корреляциялық тәуелділік. Себебі зерттеліп отырған көрсеткіштерді анықтайтын өте көп әртүрлі факторлар бір-біріне әсер ету арқылы әрдайым байланыста болады.
Корреляциялық тәуелділік
 - тің
- тің  - ке тәуелділігін
- ке тәуелділігін
 (1)
(1)
түріндегі теңдеу арқылы сипаттауға болады, мұндағы  - Х шамасының
- Х шамасының 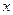 мәніне сәйкес келетін
мәніне сәйкес келетін  шамасының шартты орта мәні, ал
шамасының шартты орта мәні, ал  - қандай да бір функция. (1) теңдеу
- қандай да бір функция. (1) теңдеу  - тің
- тің  - ке таңдама регрессия теңдеуідеп аталады.
- ке таңдама регрессия теңдеуідеп аталады.
 функциясын
функциясын  - тің
- тің  - ке таңдама регрессиясыдеп, ал оның графигін
- ке таңдама регрессиясыдеп, ал оның графигін  - тің
- тің  - ке регрессиясының таңдама сызығыдеп атайды.
- ке регрессиясының таңдама сызығыдеп атайды.
Дәл осы сияқты  - тің
- тің  - ке регрессиясының таңдама теңдеуі
- ке регрессиясының таңдама теңдеуі 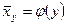 түрінде болады.
түрінде болады.
Регрессия теңдеуінің түріне және оған сәйкес сызықтық түріне байланысты қарастырылып отырған шамалардың арасындағы корреляциялық тәуелділіктің түрін анықтайды. Ол – сызықты, квадратты, көрсеткіштікболуы мүмкін.
 [немесе
[немесе 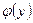 ] регрессия функциясының түрін таңдап алу – маңызды сұрақ болып табылады. Мысалы, сызықты немесе сызықты емес (көрсеткіштік, квадраттық, логарифмдік және т.б.)
] регрессия функциясының түрін таңдап алу – маңызды сұрақ болып табылады. Мысалы, сызықты немесе сызықты емес (көрсеткіштік, квадраттық, логарифмдік және т.б.)
Практикада регрессия функциясының түрін координата жазықтығында бақылаудың (  ) мәндер жұбының барлығына сәйкес келетін нүктелер жиынын тұрғызу арқылы анықтауға болады.
) мәндер жұбының барлығына сәйкес келетін нүктелер жиынын тұрғызу арқылы анықтауға болады.
Сызықтық регрессия
Регрессия функциясының, яғни  - тің
- тің  - ке (немесе
- ке (немесе  - тің
- тің  - ке) тәуелділігінің моделінің түрін таңдап алғаннан кейін, мәселен,
- ке) тәуелділігінің моделінің түрін таңдап алғаннан кейін, мәселен,  сызықтық моделін, моделдің коэффициенттерінің нақты мәндерін анықтау қажет.
сызықтық моделін, моделдің коэффициенттерінің нақты мәндерін анықтау қажет.
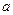 және
және  әртүрлі мәндері бойынша
әртүрлі мәндері бойынша  түріндегі шексіз көп тәуелділікті алуға болады, яғни координата жазықтығындағы шексіз көп түзулер тұрғызуға болады, ал бізге бақылап отырған мәндерге өте жақын, ең тиімді түрде сәйкес келетін тәуелділік қажет. Яғни, ең жақсы коэффициенттерді таңдау керек.
түріндегі шексіз көп тәуелділікті алуға болады, яғни координата жазықтығындағы шексіз көп түзулер тұрғызуға болады, ал бізге бақылап отырған мәндерге өте жақын, ең тиімді түрде сәйкес келетін тәуелділік қажет. Яғни, ең жақсы коэффициенттерді таңдау керек.
Ең кіші квадраттар әдісі (ЕКӘ)
 сызықтық функциясын бақылау нәтижесінде алынған мәндерге қатысты іздейміз. Бақылау мәндеріне өте жақын сәйкес келетін функцияны табу үшін ең кіші квадраттарәдісін қолданамыз.
сызықтық функциясын бақылау нәтижесінде алынған мәндерге қатысты іздейміз. Бақылау мәндеріне өте жақын сәйкес келетін функцияны табу үшін ең кіші квадраттарәдісін қолданамыз.
Мынадай белгілеулер енгіземіз: 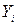 -
-  теңдеуі бойынша есептелінген мәндер,
теңдеуі бойынша есептелінген мәндер,
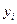 - бақылау нәтижесінде өлшелініп алынған мәндер,
- бақылау нәтижесінде өлшелініп алынған мәндер,
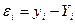 - өлшелініп алынған мәндер мен теңдеу бойынша есептелінген мәндердің айырмасы,
- өлшелініп алынған мәндер мен теңдеу бойынша есептелінген мәндердің айырмасы,  .
.
Ең кіші квадраттар әдісіндеөлшелініп алынған 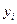 мңндері мен теідеу бойынша есептелінген
мңндері мен теідеу бойынша есептелінген 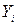 мәндерінің айырмасы ең аз (минимальды) болуы талап етіледі. Яғни, а және
мәндерінің айырмасы ең аз (минимальды) болуы талап етіледі. Яғни, а және  коэффициенттерін бақылап отырған мәндердің түзу сызықты регрессияның мәндерінен ауытқуының квадраттарының қосындысы өте аз болатындай етіп іздейміз:
коэффициенттерін бақылап отырған мәндердің түзу сызықты регрессияның мәндерінен ауытқуының квадраттарының қосындысы өте аз болатындай етіп іздейміз:
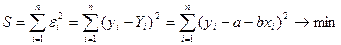 .
.
Бұл 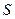 - фукнкциясы а және
- фукнкциясы а және  аргументтеріне тәуелді екі айнымалының функциясы болып табылады.
аргументтеріне тәуелді екі айнымалының функциясы болып табылады. 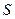 - функциясын туындының көмегі арқылы экстремумға зерттей отырып, бұл функция минимальды мәнді, егер а және
- функциясын туындының көмегі арқылы экстремумға зерттей отырып, бұл функция минимальды мәнді, егер а және  коэффициенттері мынадай жүйенің шешімі болған жағдайда қабылдайтынын дәлелдеуге болады.
коэффициенттері мынадай жүйенің шешімі болған жағдайда қабылдайтынын дәлелдеуге болады.
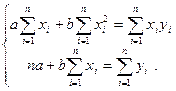 (*)
(*)
Бұл жүйе ең кіші квадраттар әдісінің қалыпты теңдеулер жүйесідеп аталады.
Егер қалыпты теңдеулердің екі жағын да n – ге бөлсек, онда

аламыз.
 , (**)
, (**)
екенін ескерсек,

аламыз. Бұдан  , а- ның мәнін бірінші теңдеуге қою арқылы
, а- ның мәнін бірінші теңдеуге қою арқылы
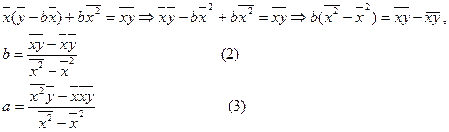
аламыз.  - регрессия коэффициенті, а- регрессия теңдеуінің бос мүшесі.
- регрессия коэффициенті, а- регрессия теңдеуінің бос мүшесі.
Алынған түзу теориялық регрессия сызығының бағасы болып табылады.
 .
.
Сонымен,  сызықтық регрессияның теңдеуі.
сызықтық регрессияның теңдеуі.
Регрессия тура 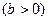 және кері
және кері  болуы мүмкін.
болуы мүмкін.
Егер бірінші параметрдің мәндері өскенде, екінші параметрдің мәндері өсетін болса, онда ол тура регрессия,ал бір параметрдің мәндері өскенде, екінші параметрдің мәндері кемитін болса, онда ол – кері регрессияныбілдіреді.
1-мысал.n елді мекендерінде тәулігіне тұщы суды санитарлы-тұрмыстық мұқтаждыққа пайдаланудың Х (л/адам) берілген деңгейіне жалпы ауру-сырқаулықтың  (%) деңгейінің көптеген мәні сәйкес келеді. (% - ке шаққанда). Бұл жағдайда Х-тің өсуіне
(%) деңгейінің көптеген мәні сәйкес келеді. (% - ке шаққанда). Бұл жағдайда Х-тің өсуіне  -ң кемуісәйкес келетіні байқалады. Бұл – кері, теріс корреляциялық байланыс. (1 сурет).
-ң кемуісәйкес келетіні байқалады. Бұл – кері, теріс корреляциялық байланыс. (1 сурет).
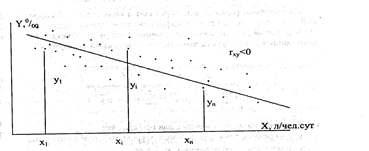 |
1-сурет. Х факторы мен  параметрінің арасындағы кері корреляциялық байланысты бақылау өрісі.
параметрінің арасындағы кері корреляциялық байланысты бақылау өрісі.
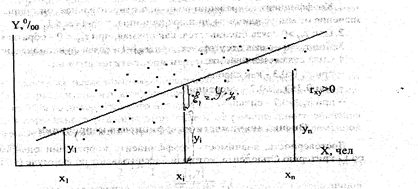 |
2-мысал.Өндіріс аймағындағы жұмыс орнының тығыздығы Х (адам) өскен сайын жұқпалы ауру деңгейінің
 (% пен) өсуі – тура, оң корреляциялық байланыстың мысалы болып табылады (2 сурет).
(% пен) өсуі – тура, оң корреляциялық байланыстың мысалы болып табылады (2 сурет).
2-сурет.Х факторы мен  параметрінің арасындағы тура корреляциялық байланысты бақылау өрісі.
параметрінің арасындағы тура корреляциялық байланысты бақылау өрісі.
Регрессия коэффициентінің мәнділігі туралы жорамалды тексеру
Біз бақылау нәтижесінде алынған өлшемдерді сипаттайтын модельді алдық, енді оның дұрыс екендігін анықтау керек.
Регрессиялық талдаудың моделі:  мұндағы
мұндағы 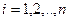 түрінде болады.
түрінде болады. 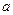 -
-  бойынша ығысуды сипаттайтын параметр,
бойынша ығысуды сипаттайтын параметр,  - регрессия коэффициенті, функция графигінің Х бойынша ығысуын сипаттайтын параметр,
- регрессия коэффициенті, функция графигінің Х бойынша ығысуын сипаттайтын параметр, 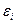 - кездейсоқ айнымалының корреляциялық тәуелділікпен байланыспаған (коррелденбеген) қателіктері.
- кездейсоқ айнымалының корреляциялық тәуелділікпен байланыспаған (коррелденбеген) қателіктері.
Регрессиялық талдауда  регрессия коэффициентінің және
регрессия коэффициентінің және 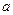 бос мүшесінің мәнділігі туралы жорамалды тексереді.
бос мүшесінің мәнділігі туралы жорамалды тексереді.
1.  және
және  жорамалдарын анықтаймыз.
жорамалдарын анықтаймыз.
 :
: 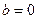 (айнымалылар арасында сызықтық тәуелділік жоқ)
(айнымалылар арасында сызықтық тәуелділік жоқ)
 :
:  .
.
2.  мәнділік деңгейін береміз.
мәнділік деңгейін береміз.
3. Критерийдің статистикасы
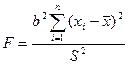 , мұндағы
, мұндағы  ,
, 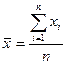 және
және  .
.
4. Критикалық нүктелер және критикалық аймақ 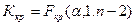 . F статистикасы 1 және (n-2) бос дәрежелерімен Фишер таралуына тең.
. F статистикасы 1 және (n-2) бос дәрежелерімен Фишер таралуына тең.
5. Егер 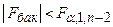 , онда Н0 теріске шығарылады, яғни сызықтық тәуелділік мәнді деген қорытынды жасауға болады.
, онда Н0 теріске шығарылады, яғни сызықтық тәуелділік мәнді деген қорытынды жасауға болады.
Егер 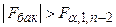 , онда бізде Н0- ді қабылдамауға негіз жоқ, яғни сызықтық тәуелділік – мәнді емес немесе берілгендерді сызықтық регрессия моделімен сипаттауға болмайды.
, онда бізде Н0- ді қабылдамауға негіз жоқ, яғни сызықтық тәуелділік – мәнді емес немесе берілгендерді сызықтық регрессия моделімен сипаттауға болмайды.
Сызықтық корреляция.
Корреляциялық талдау.
Корреляциялық талдау Х және  кездейсоқ шамаларының арасындағы байланыстың дәрежесін анықтаумен айналысады.
кездейсоқ шамаларының арасындағы байланыстың дәрежесін анықтаумен айналысады.
Екі кездейсоқ шамалар үшін тәжірибе нәтижесінде алынған деректердің корреляциялық талдауы мынадай негізгі тәсілдерді қарастырады:
1. Корреляциялық таңдама коэффициентін есептеу.
2. Корреляциялық кесте құру.
3. Байланыс мәнділігі жөніндегі статистикалық жорамалды тексеру.
Анықтама.Егер  және
және  регрессия функцияларының екеуі де сызықтық болса, онда Х және
регрессия функцияларының екеуі де сызықтық болса, онда Х және  кездейсоқ шамаларының арасындағы корреляциялық тәуелділік сызықтық корреляциядеп аталады.
кездейсоқ шамаларының арасындағы корреляциялық тәуелділік сызықтық корреляциядеп аталады.
Корреляцияның таңдама коэффициенті.
Кездейсоқ шамалар арасындағы корреляциялық тәуелділіктің ерекшеліктерін толық сипаттау үшін бұл тәуелділіктің түрін анықтау және ол сызықтық тәуелділік болған жағдайда оның күшін регрессия коэффициентінің шамасы бойынша бағалау жеткіліксіз. 3-суретте екі сызықтық корреляциялық тәуелділіктің  -тің Х- ке графиктік суреттемесі келтірілген және регрессияның сәйкес түзу сызықтары бейнеленген.
-тің Х- ке графиктік суреттемесі келтірілген және регрессияның сәйкес түзу сызықтары бейнеленген.
 |  | ||||||
 | |||||||
 | |||||||
|



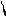

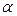


 |
а) x б) x
3-сурет
Мұндағы  және Х шамаларының арасында корреляциялық тәуелділіктің күші бірдей (ол регрессия сызықтарының сәйкес түзулерінің ОХ осіне енкею бұрыштарының теңдігінен шығады). Алайда 3 а) сур. кескінделген корреляциялық тәуелділік үшін бақылау нүктелерінің регрессия сызығына қарасты шашылуы,3 б) сур. кескінделген корреляциялық тәуелділікке қарағанда аз. Мұндай жағдайда, қарастырылып отырған корреляциялық тәуелділіктер тығыздығыменерекшеленеді деп айтады, және 3 а) сур. кескінделген корреляциялық тәуелділік 3 б) сур. келтірілген корреляциялық тәуелділікке қарағанда тығызырақ деп саналады.
және Х шамаларының арасында корреляциялық тәуелділіктің күші бірдей (ол регрессия сызықтарының сәйкес түзулерінің ОХ осіне енкею бұрыштарының теңдігінен шығады). Алайда 3 а) сур. кескінделген корреляциялық тәуелділік үшін бақылау нүктелерінің регрессия сызығына қарасты шашылуы,3 б) сур. кескінделген корреляциялық тәуелділікке қарағанда аз. Мұндай жағдайда, қарастырылып отырған корреляциялық тәуелділіктер тығыздығыменерекшеленеді деп айтады, және 3 а) сур. кескінделген корреляциялық тәуелділік 3 б) сур. келтірілген корреляциялық тәуелділікке қарағанда тығызырақ деп саналады.
Мысалы, орта мектеп оқушыларының жас мөлшері (  ) мен олардың мектепте оқып жатқан оқу жылының (Х) арасындағы корреляциялық тәуелділік, сол сияқты жоғары оқу орнындағы студенттерінің жас мөлшерінің оқу жылына тәуелділігіне қарағанда тығыздау болатыны айқын, себебі жоғары оқу орнында бір жылда оқып жатқан студенттердің арасында жас мөлшерлерінде бір сыныпта оқитын оқушыларға қарағанда үлкен алшақтық (шашылу) болатыны байқалады.
) мен олардың мектепте оқып жатқан оқу жылының (Х) арасындағы корреляциялық тәуелділік, сол сияқты жоғары оқу орнындағы студенттерінің жас мөлшерінің оқу жылына тәуелділігіне қарағанда тығыздау болатыны айқын, себебі жоғары оқу орнында бір жылда оқып жатқан студенттердің арасында жас мөлшерлерінде бір сыныпта оқитын оқушыларға қарағанда үлкен алшақтық (шашылу) болатыны байқалады.
Таңдама бақылау нәтижелері бойынша Х және  шамаларының арасындағы сызықтық корреляциялық тәуелділіктердің тығыздығын бағалау үшін сызықтық корреляцияның таңдама коэффициентіұғымы енгізіледі, және ол
шамаларының арасындағы сызықтық корреляциялық тәуелділіктердің тығыздығын бағалау үшін сызықтық корреляцияның таңдама коэффициентіұғымы енгізіледі, және ол
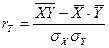 (4)
(4)
формуласымен анықталады, мұндағы 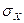 және
және 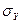 - Х және
- Х және  шамаларының сәйкес таңдама орта квадраттық ауытқулары және олар
шамаларының сәйкес таңдама орта квадраттық ауытқулары және олар
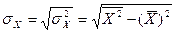
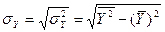 (5)
(5)

формулаларымен есептелінеді. Айта кету керек, сызықтық корреляцияның таңдама коэффициенті 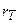 -ң негізгі мағынасы, ол сәйкес сызықтық корреляцияның бас коэффициентінің
-ң негізгі мағынасы, ол сәйкес сызықтық корреляцияның бас коэффициентінің  эмпирикалық бағасын береді:
эмпирикалық бағасын береді:
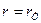 (6)
(6)

формулаларын ескерсек,  - тің Х- ке сызықтық регрессиясының таңдама теңдеуі мына түрде болады:
- тің Х- ке сызықтық регрессиясының таңдама теңдеуі мына түрде болады:
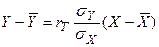 (7)
(7)
мұндағы  (регрессия коэффициенті)
(регрессия коэффициенті)
Сол сияқты Х - тің  -ке сызықтық регрессияның теңдеуін жазуға болады:
-ке сызықтық регрессияның теңдеуін жазуға болады:
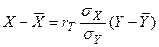 (8)
(8)
Сызықтық корреляцияның таңдама коэффициентінің негізгі қасиеттері
1. Сызықтық корреляциялық тәуелділікпен байланыспаған екі шаманың корреляция коэффициенті нөлге тең.
2. Сызықтық корреляциялық тәуелділікпен байланысқан екі шаманың корреляциялық коэффициенті 1-ге тең, егер тәуелділік тура (өспелі) болса және -1-ге тең, егер тәуелділік кері (кемімелі) болса;
3. Сызықтық корреляциялық тәуелділікпен байланысқан екі шаманың корреляциялық коэффициентінің абсолюттік шамасы 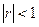 теңсіздігін қанағаттандырады. Егер корреляциялық тәуелділік өспелі болса, онда корреляция коэффициенті оң, егер корреляциялық тәуелділік кемімелі болса, онда корреляция коэффициенті теріс.
теңсіздігін қанағаттандырады. Егер корреляциялық тәуелділік өспелі болса, онда корреляция коэффициенті оң, егер корреляциялық тәуелділік кемімелі болса, онда корреляция коэффициенті теріс.
4.  1-ге неғұрлым жақын болса,
1-ге неғұрлым жақын болса, 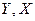 шамаларының арасындағы түзу сызықты корреляция соғұрлым тығызырақ.
шамаларының арасындағы түзу сызықты корреляция соғұрлым тығызырақ.
Корреляциялық байланыс сипатына қарай туражәне кері,күшіне қарай күшті, орташа, әлсізболуы мүмкін.
Параметрлер арасындағы байланыстың күші мен сипаты.
| Байланыс күші | Байланыс сипаты | |
| Тура (+) | Кері (-) | |
| Толық | -1 | |
| Күшті | 0,7 ден 1 ге дейін | -0,7 ден -1 ге дейін |
| Орта | 0,699 ден 0,3 ге дейін | -0,699 ден -0,3 ге дейін |
| Әлсіз | 0,299 ден 0 ге дейін | -0,299 ден 0 ге дейін |
| Байланыс жоқ |
Корреляцияның таңдама коэффициентінің
мәнділігі туралы жорамалды тексеру.
Статистикалық өзара байланыс жөнінде сөз болғанда, оның бар болуынемесе жоқ болуы,бағытының болуы (оң немесе теріс) және күшінің сипатымен (күшті, әлсіз) анықталады. Егер зерттеу нәтижесінде нөлдік жорамал теріске шығарылмаса, онда «өзара байланыс жоқң. Нөлдік жорамал теріске шығарылған жағдайда кездейсоқ шамалардың арасында байланыс бар делінеді.
1. Н0 және Н1 жорамалдарын тағайындайық:
 (яғни, корреляция жоқ),
(яғни, корреляция жоқ),
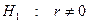 .
.
2.  мәнділік деңгейін береміз.
мәнділік деңгейін береміз.
3. Критерияның статистикасы: 
4.  мұндағы
мұндағы 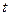 -
-  бос дәрежесімен Стьюдент таралуы болатын статистика.
бос дәрежесімен Стьюдент таралуы болатын статистика.
5.  болғанда Н0 жорамалы:
болғанда Н0 жорамалы: 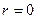
 мәнділік деңгейімен теріске шығарылады. Демек, параметрлердің арасында мәнді корреляция бар.
мәнділік деңгейімен теріске шығарылады. Демек, параметрлердің арасында мәнді корреляция бар.
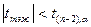 болғанда Н0 жорамалын теріске шығаруға негіз жоқ, яғни параметрлердің арасында мәнді корреляция жоқ.
болғанда Н0 жорамалын теріске шығаруға негіз жоқ, яғни параметрлердің арасында мәнді корреляция жоқ.
3 мысал.х және у шамаларының өлшем нәтижелері кестеде берілген.

| -2 | ||||
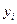
| 0,5 | 1,5 |
1) y-ң x-қа түзу регрессиясының таңдама теңдеуін;
2) Регрессия сызығын тұрғызу;
3) Корреляцияның таңдама коэффициентін есептеу;
4) Корреляциялық тәуелділіктің сипаты мен күшін анықтау.
Шешуі.Мұнда n=5
1) а) Х пен  -тің арасында
-тің арасында 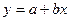 сызықты тәуелділігі бар деп ұйғарып, ең кіші квадраттар әдісімен
сызықты тәуелділігі бар деп ұйғарып, ең кіші квадраттар әдісімен 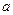 және
және Тапсырмалар.
| <== попередня сторінка | | | наступна сторінка ==> |
| Уилкоксон критерийі | | | ПРИЛОЖЕНИЯ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |