• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

при отсутствии логики

Т Е О Р И Я

ОТНОСИТЕЛЬНОСТИ

– реальность или выдумка

при отсутствии логики

Сумы

ББК 22.311

Г94

УДК 530.1

Міністерство освіти і науки України.

Державний департамент інтелектуальної власності.

Свідоцтво про реєстрацію авторського права на твір

№11409 від 27.10.2004 р.

Книга «Теория относительности – реальность или выдумка

при отсутствии логики».

Автор – Гулий Андрій Маркович.

Гулий А. М.

Г94 Теорія відносності – реальність чи вигадка без логіки.

Суми, видавництво «МакДен», рос. мов., 2006. – 140 с.

ISBN 955–7222–52–7

Серед вчених існує думка, що теорію відносності мало хто розуміє. Ця книга допоможе кожному зрозуміти цю теорію. В книзі розглядаються фундаментальні положення теорії відносності, на яких базується уся теорія.

Матеріал викладений на рівні, який доступний кожному. Математичний матеріал не виходить за межі програм загальноосвітніх навчальних закладів

Среди ученых есть мнение, что теорию относительности понимают только немногие. Данная книга поможет каждому, кто прочитает ее, понять эту теорию. В книге рассмотре­ны фундаментальные положения теории относительности, на которых построена вся теория.

Материал книги изложен на доступном каждому уровне. Математический материал не выходит за пределы програм­мы общеобразовательных учебных заведений.

ББК 22.311

ISBN 955–7222–52–7 © Гулый А. М., 2004 г.

© Издательство “МакДен”, 2006 г.

К ЧИТАТЕЛЯМ

Теория относительности состоит из двух частей. Первая часть называется специальная (или частная) теория относительности, вторая часть – общая теория относи­тельности. Мы же остановимся только на специальной те­ории относительности и только на ее фундаментальных положениях и уравнениях, на которых построена вся тео­рия. Автор теории Альберт Эйнштейн.

Работы Эйнштейна по специальной теории относительнос­ти практически полностью собраны в книге "Альберт Эйн­штейн. Собрание научных трудов, том 1, работы по теории относительности", издательство "Наука", Москва, 1965 год. В дальнейшем выдержки из этой книги и ссылки на книгу не будут снабжаться полным названием ее и спе­циальными указателями на нее.

Материал нашей книги изложен так, чтобы он был доступным и понятным каждому. Поэтому решения математичес­ких уравнений изложено в развернутом виде полностью. Но это нужно не каждому. Поэтому рекомендуем зря не вникать в само решение, пропускать его мимо внимания, и обращать внимание только на полученный результат. Это облегчит процесс чтения. И только там, где возникнет особый интерес к решению, или сомнение в правильности решения, надо внимательно просмотреть весь процесс ре­шения.

СИСТЕМЫ ОТСЧЕТА

Здесь и в дальнейшем довольно часто будет речь ид­ти о системах отсчета. Поскольку не все четко представ­ля­ют что это такое, имеется смысл несколько остановиться на этом понятии.

Для определения положения какого-либо объекта в прост­ранстве используются системы координат. Часто их назы­вают системами отсчета, или просто системами. Например, чтобы объяснить где размещена электрическая лампочка в вашей комнате, вы называете три размера: 2,1 метра от пола, 2 метра от стены, которая перед вами, и 3 метра от стены, которая слева от вас. Это и есть координаты вашей лампочки в вашей комнате, которые точно указывают то место, где находится лампочка. Две стены и пол ком­наты являются в данном случае системой координат (или системой отсчета расстояний до лампочки).

Системы координат бывают прямоугольные, косоугольные, полярные и др. Наиболее употребительной и в то же вре­мя наиболее простой является прямоугольная система ко­ординат. На ней мы и остановимся.

Прямоугольная система координат представляет собой систему, состоящую из трех взаимно перпендикулярных плоскостей. Вернемся опять в комнату. Станем лицом к стене, которая с южной стороны. Тогда южная стена пред­ставляет собой одну плоскость, восточная стена (слева от вас) – вторая плоскость и пол – третья. Называются плоскости: та, что перед вами, – фронтальная, та, что слева, – боковая, та, что под вами (пол), – горизонталь­ная.

Линии пересечения плоскостей являются осями коорди­нат. А точка пересечения осей является началом коорди­нат. От этой точки отсчитываются координаты. Обычно на­чало обозначается буквой О,которая одновременно озна­чает и число нуль. Концы осей не ограничены, оси прос­тираются в бесконечность. Линия пересечения фронталь­ной и горизонтальной плоскостей называется осью абс­цисс или осью ОХ. По этой оси откладывается координа­та x. Линия пересечения фронтальной и боковой плоскос­тей называется осью ординат или осью ОY. По этой оси откладывается координата y. Линия пересечения боковой и горизонтальной плоскостей называется осью аппликат или осью OZ. По этой оси откладывается координата z. Чаще положительными считаются координаты, которые отк­ладываются на осях справа, вверху и спереди от начала координат, а отрицательными – слева, внизу и сзади от начала координат. При таком расположении осей координат фронтальная плоскость называется плоскостью ХОY, горизонтальная – ХОZ и боковая – YОZ.

Хотя в литературе часто бывает принято другое распо­ложение осей, автор считает предложенное здесь распо­ложение наиболее удобным. Это объясняется тем, что при переходе к координатной системе на плоскости не требу­ется менять названия и значения осей. Достаточно счи­тать, что координата z равна нулю.

Рассмотрим что представляют собой координаты какого-нибудь объекта. Например, той же электрической лампоч­ки в вашей комнате. Для этого отметим на полу и на сте­нах (теперь уже плоскости ХОY, XOZ и YOZ) точки, че­рез которые проходят прямые линии от лампочки перпен­дикулярно к указанным плоскостям. Източки на плоскос­ти ХОY проведем прямые линии перпендикулярно к осям ОХ и ОY (или, что то же самое, параллельно к осям OY и OX)до пересечения с осями. Расстояния, измеренные от на­чала координат до точек пересечения, и будут координатами х и у вашей лампочки. Проделав то же самое на плоскости YOZ, найдем координаты y на оси ОY и z на оси OZ. Таким же образом на плоскости ХOZ найдем коор­динаты х и z.

Наблюдательный читатель поймет, что тот же результат получим и в том случае, если опустим перпендикуляры от лампочки и сразу непосредственно на оси.

На чертежах, как правило, изображаются только те оси, которые используются в тексте.

Выражение движущаяся (или неподвижная) система отсче­та не означает, что это движется обязательно пустая система. Под этим всегда подразумевается, что движется какой-то объект, и вместе с ним движется связанная с ним система.

Координатные системы, которые движутся прямолинейно и равномерно (т.е. без ускорения), называются инерциальными системами.

ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Среди ученых бытует мнение, что теорию относительно­сти понимают лишь немногие. Поэтому и не удивляйтесь, если вы ее не можете понять. Не одни вы в таком положении. Даже многие ученые в своих трудах по теории относитель­ности зачастую приводят противоречивые толкования ее положений. Что же это за такая трудно одолимая наука?

Для тех, кто не знаком с теорией относительности, из­лагаем в самой популярной форме основные ее положения. Теория относительности – это научная теория в области физики. Ее создатель Альберт Эйнштейн. В соответствии с этой теорией свет распространяется относительно каждого тела с одинаковой скоростью, равной почти 300 000 километров за секунду, независимо от того, движется это тело или остается неподвижным. Длина движущейся линейки меньше, чем ее же длина, когда она неподвижна. Время для движущихся объектов течет медленнее, чем в случае, когда они неподвижны. Масса движущегося тела больше, чем в случае, когда оно неподвижно. Если на стыках рельс в начале и в конце рельса колеса движуще­гося поезда стукнули одновременно, о чем отметили при­боры на поезде, то на земле приборы отметят, что коле­са стукнули неодновременно. И т.д. Как видим, предста­вить, как это все получается, практически невозможно. Поэтому эту теорию и трудно понять. Но разберемся во всем по порядку.

Физика, как наука, достигла бурного расцвета в XIX-ХХ столетиях. К концу XIX столетия были твердо установле­ны механические законы природы и значительно изучены электрические, магнитные и электромагнитные явления. В частности, много внимания уделялось изучению природы света. На смену корпускулярной теории света пришла вол­новая теория, сначала механическая, а затем электромаг­нитная. Считалось, что все пространство Вселенной за­полнено эфиром, который неподвижен в пространстве. Свет представляет собой колебания эфира (как звук представ­ляет собой колебания воздуха).

Поскольку эфир неподвижен в пространстве, а Земля движется по своей орбите вокруг Солнца, то естественно предположить, что Земля движется сквозь эфир подобно тому, как движется любой предмет сквозь воздух. Следо­вательно, по отношению к Земле должен перемещаться эфир с той же скоростью, с какой Земля перемещается относительно эфира. Подобные рассуждения привели уче­ных к мысли попытаться определить скорость движения Земли путем измерения скорости эфирного ветра. Так как свет представляет собой колебания эфира, то волны этих колебаний (т.е. свет) распространяются относительно этого эфира. В таком случае движущийся эфир должен уносить с собой и свет. Путем измерения скорости, с ко­торой уносится свет, определяется скорость движения Земли. Такое измерение произвел Майкельсон на опыте, который он повторил, а затем и другие ученые повторили несколько раз в 1881-1927 годах. В результате измере­ний выяснилось, что эфирный ветер отсутствует. Можно было объяснить этот результат тем, что эфир полностью увлекается воздухом. Но этому противоречил ранее про­изведенный Физо опыт с водой. В результате этого опыта было установлено, что движущаяся вода увлекает эфир только частично, а не полностью. Следовательно, воздух тем более не может увлекать эфир полностью.

Таким образом, в ученом мире к концу XIX столетия по­явилась новая нерешенная проблема. Кроме того, в элект­родинамике движущихся зарядов также возникли проблемы. При попытках решить появившиеся проблемы предлагались и отвергались разные предположения. А тем временем уче­ные, которые думали больше о практической стороне дела, занимались больше количественной стороной вопроса и создавали эмпирические формулы, пригодные для произ­водства математических расчетов. Это формулы, подогнан­ные под результаты опытов.

Для объяснения отрицательного результата опыта Майкельсона Фитцджеральд и Лоренц (независимо друг от друга) пришли к выводу, что если считать, что при движе­нии размеры тела уменьшаются в направлении движения, то прибор Майкельсона не сможет обнаружить эфирный ветер. Это и получено на опыте. И хотя после усовершенствова­ния прибора выяснилось, что такое объяснение не годит­ся, все равно в электронной теории Лоренца это сокраще­ние нашло обоснование и применение. Следовательно, в кругу ученых уже было мнение, что движущиеся тела сок­ращают свои размеры в направлении движения в соответствии с формулой

,

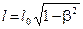где l₀–длина тела, когда оно неподвижное,

l –длина того же тела, когда оно движется,

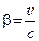– отношение скорости v движения тела к скорости с распространения света.

Однако этого оказалось мало. Для объяснения других опытов необходимо было предположить, что в движущихся телах процессы протекают медленнее. Другими словами, движущиеся часы идут медленнее. И тоже в соответствии с формулой

,

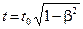где t₀–время, отсчитанное неподвижными часами,

t – время, отсчитанное такими же, но движущимися часами.

В конце XIX столетия Лоренц, руководствуясь указан­ными предположениями, создал свою теорию. Эта теория достаточно правильно объясняла почти все явления в оп­тике и электродинамике, объясняла опыт Физо. Поэтому эта теория была господствующей в те времена. Для связи движущихся объектов с неподвижными Лоренц создал сис­тему эмпирических уравнений, которые потом стали назы­ваться преобразованиями Лоренца,

,

,

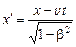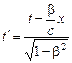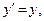
где .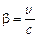

В этих уравнениях считается, что х, у, z, t являются координатами и временем в неподвижной системе отсче­та, х', y', z' являются координатами в движущейся системе отсчета, v –скорость, с которой движущаяся система дви­жется относительно неподвижной системы, с –скорость распространения света в вакууме, t' –фиктивная вспомо­гательная величина, не имеющая никакого реального зна­чения. Лоренц называл ее местным временем.

Эйнштейн, как и многие ученые, верил в силу теории Лоренца и в его преобразования, хотя теория и имела немало недостатков. И главный тот, что её формулы были эмпирическими, а не следовали из теории.

Если проводить разные математические манипуляции с преобразованиями Лоренца, то можно получить и интерес­ные результаты. Например, если рассматривать распрост­ранение света вдоль оси OХ в положительном направле­нии, то для начала луча справедливо уравнение

.

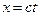Это значит, что если в начале координат вспыхнул свет в момент времени, когда t = 0, то в любой другой момент времени свет дойдет до точки, координата которой х равна расстоянию сt. Разделив первое преобразование на второе и подставляя получим

Следовательно

.

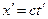Получается, что если в неподвижной системе , то и в движущейся системе 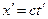. Если посчитать, что t' нефиктивная величина, а реальное время в движущейся сис­теме, то выходит, что свет распространяется с одинако­вой скоростью с как в неподвижной, так и в движущейся системе, несмотря на то, что система движется в том же направлении, в каком и свет распространяется. Если это принять за реальность, то получается, что относительно Земли свет тоже распространяется со скоростью с неза­висимо от того, что Земля движется. А это значит, что на опыте Майкельсона нельзя было получить ничего дру­гого, кроме отрицательного результата. Очень заманчиво. Без всякой мороки получается объяснение опыта Майкельсона.

Очень уж эти результаты математических манипуляций совпадают с постулатами Эйнштейна. Так и хочется поду­мать, что Эйнштейн тоже произвел такую манипуляцию с преобразованиями Лоренца и результат представил как постулаты. Но подумать, не имея на то оснований, конеч­но можно, авот утверждать не только нельзя, а и непри­лично. Оставим этот вопрос для историков.

На странице 66 Эйнштейн пишет "Следовало лишь понять, что введенную Г. А. Лоренцом вспомогательную величину, названную им "местным временем", на самом деле следует определить как "время". С таким определением времени основные уравнения теории Лоренца будут удовлетворять принципу относительности". "Тогда гипотеза Лоренца и Фитцджеральда окажется необходимым следствием теории". Из этих слов Эйнштейна получается, что одной из глав­ных задач при создании его теории относительности яв­ляется доказательство того, что преобразования Лоренца не являются эмпирическими уравнениями, а являются частью теории. Для этого надо их вывести теоретически.

Постулаты Эйнштейна.

1. Никакими опытами внутри лаборатории (имеется в ви­ду внутри системы отсчета, которая связана с лаборато­рией) нельзя обнаружить движется ли лаборатория с пос­тоянной скоростью или нет. Это значит, что во всех взаимно движущихся лабораториях все процессы протекают одинаково.

2. Свет в вакууме распространяется всегда с одинако­вой скоростью с относительно приемника света (опять же относительно системы отсчета) независимо от того, движется ли приемник с постоянной скоростью или нет.

Как видим, пример для первого постулата – это Земля и опыт Майкельсона, с помощью которого не удалось обнаружить ее движение, хотя известно, что она движется хотя бы по орбите. Примером для второго постулата явля­ется все та же Земля, относительно которой свет расп­ространяется во все стороны с одинаковой скоростью с,хотя Земля и движется. Это и явилось причиной, из-за которой не удалось обнаружить движение Земли с помощью прибора Майкельсона. Собственно говоря, второй посту­лат вытекает из первого.

Эти постулаты и легли в основу теории относительнос­ти.

Но постулаты сами по себе – еще не теория. Чтобы они были признаны теорией, надо, по крайней мере, хотя бы доказать, что не они выведены из преобразований Лорен­ца, а наоборот, преобразования Лоренца выведены из по­стулатов, а значит преобразования Лоренца являются следствием постулатов. Тогда постулаты смогут претен­довать на роль теории. Но почему именно преобразования Лоренца? Да потому, что в те времена эти преобразова­ния достаточно хорошо способствовали объяснению многих опытных данных. Кроме того, они же приводят и к посту­латам при определенных математических манипуляциях с ними. Достаточно этот путь пройти в обратном направле­нии и получатся преобразования Лоренца. Эйнштейн сде­лал вывод преобразований. Причем, не один раз, а трижды. В книге изложены все три варианта вывода. На них мы остановимся позже.

Размышляя над постулатами, Эйнштейн приходит к выводу, что для того, чтобы свет распространялся одинаково и относительно неподвижного эфира (т.е. в неподвижной системе координат), и относительно движущейся Земли (т.е. в движущейся системе координат), необходимо, что­бы эфир был одновременно и неподвижным, и двигался вместе с Землей. Эйнштейн посчитал это абсурдом и уп­разднил эфир, а следовательно, и волновую теорию света. Таким образом, все объекты Вселенной освободились от неподвижной среды и стали вольно передвигаться в прост­ранстве. А свет превратился в фотоны и стал гоняться за каждым объектом со скоростью с. В том числе и за каждым комаром в комарином рое.

Пытаясь объяснить, как же это может происходить ре­ально, Эйнштейн рассматривает следующий пример. Пусть две координатные системы движутся одна относительно другой. И пусть в момент времени, когда совпали начала координат, в этом общем начале координат вспыхнул свет. В этот же момент время t =0и t' = 0. Тогда в произволь­ный момент времени фронт волны света будет представлять собой сферу с радиусом ct в неподвижной системе и ct' в движущейся, центрами же этой общей сферы будут нача­ла координат О и О',которые в данный момент уже не совпадают. Разумеется, абсурдно думать, что одна сфера может иметь два разных центра. Для решения этой проб­лемы Эйнштейн вводит в теорию еще одно предположение, что события, одновременные в одной системе отсчета, не являются одновременными в другой системе отсчета. Пред­положить то он предположил, а вот как с помощью этого предположения доказать, что ct и ct' являются радиусами одной и той же сферы, он не сказал. Читатель сам может попытаться решить этот вопрос.

Таким образом, для решения одной проблемы (отрицательный результат опыта Майкельсона) Эйнштейн наделал много других проблем (как он думал, новых законов при­роды).

1. Эфира нет. Надо заново решать вопрос о природе света и электромагнитных волн.

2. Все системы отсчета равнозначны независимо от их движения. Если бы наблюдатель смог перемещаться из од­ной системы в другую, то он бы отметил, что в каждой системе все процессы протекают одинаково.

3. Свет во всех системах распространяется со скорос­тью с во все стороны одинаково независимо от взаимно­го движения этих систем.

4. Время у каждой системы принадлежит только этой системе и протекает одинаково во всех системах только для тех наблюдателей, которые находятся в этих систе­мах, тогда как для этих же наблюдателей время в других системах течет по-разному. У каждого летящего комара свое время.

5. События, одновременные в одной системе, являются неодновременными в другой системе.

Причем, все сказанное в этих предположениях выполня­ется только в тех системах отсчета, которые движутся равномерно и прямолинейно. Такие системы называются инерциальными.

ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ

Что такое движущаяся и неподвижная система отсчета? Что такое движение? Движение – это перемещение одного объекта относительно другого.

Давайте представим очень отдаленный участок пространс­тва, где нет материальных тел, гравитационных полей, эфира и т.д., т.е., где нет ничего, кроме одного мате­риального тела. Это может быть или песчинка, или пла­нета, или звезда, или просто вы, читатель, собственной персоной. Можно ли в данном случае определить движется ли тело, или нет? И если движется, то куда, в каком на­правлении? И можно ли в данном случае однозначно опре­делить направление? Разумеется, ничего этого сделать невозможно. Нет ориентиров.

Это на земле мы привыкли легко определять состояние движения того или иного объекта. Здесь есть ориентиры, например, дорога, стороны света, верх, низ и т.д. Мы с самого детства считаем Землю неподвижной. И совсем не задумываемся почему Землю считаем неподвижной. А ведь Земля движется, как и все остальные небесные тела.

А теперь давайте представим, что на выбранном нами участке не одно, а два тела, которые движутся друг от­носительно друга. В этом случае мы можем отметить толь­ко движение первого тела относительно второго, или на­оборот, движение второго тела относительно первого. И только. А куда и как они движутся вдвоем вместе, мы ни­как не можем определить. Тем более, не можем определить покоится ли хоть какое-нибудь из них.

Не появится возможность найти неподвижное тело и в случае, если на участке будет много движущихся тел. Ка­ждое из этих тел в равной степени может считаться не­подвижным, но это не значит, что хоть одно из них дей­ствительно неподвижно. Все они находятся в относитель­ном движении. Вселенная и представляет собой простран­ство, в котором огромное количество тел находится в движении друг относительно друга. И не найти ни одного тела во Вселенной, о котором мы могли бы сказать, что оно неподвижно.

Из сказанного вытекает очень важный вывод. Движение бывает только относительным. Если мы говорим, что дви­жется поезд, автомобиль или самолет, то всегда понима­ем, что движутся они относительно поверхности Земли, и совсем не учитываем то, что Земля тоже движется. Напри­мер, если предположить, что ось Земли неподвижна, а ав­томобиль едет на запад со скоростью 66 км/час, то в пространстве (при нашем предположении) он будет пере­мещаться в обратном направлении со скоростью 1600 км/час. А другой автомобиль, стоящий в гараже, в данном случае движется со скоростью 1666 км/час, т.е. движется быст­рее первого. Это происходит за счет вращения Земли. А если учесть еще и движение Земли вокруг Солнца, и дви­жение Солнца вместе с Землей в Галактике, и движение Галактики, и т.д., то становится ясно, что то движение автомобиля, которое мы отмечаем, находясь на земле, представляет со­бой ничтожную долю скорости в движении автомобиля в пространстве. А может быть автомобиль совсем не движется, а движется вся Вселенная относительно автомобиля. Конечно такое трудно представить. Автомобиль ведь маленький, а Все­ленная большая. Но давайте несколько сравняем размеры. Что движется, Юпитер относительно Земли, или Земля от­носительно Юпитера? И другое – американцы относительно нас, или мы относительно американцев? Движется здесь каждый относительно другого.

Скорость движения любого объекта можно определить только относительно другого объекта. Движение всегда относительно.

Эйнштейн этого или не понимал, или не хотел понять. Скорее всего, первое. Например, в своей статье "К элек­тродинамике движущихся тел" на стр. 19 он пишет следу­ющее "Если в точках А и В системы K помещены покоящие­ся синхронно идущие часы, наблюдаемые в покоящейся си­стеме, и если часы из точки A двигать по линии, соеди­няющей ее с В,в сторону последней со скоростью v, то по прибытии этих часов в В они уже не будут более идти синхронно с часами в В. Часы, передвигавшиеся из A в В,отстают по сравнению с часами, находящимися в В ". Детская логика. Вижу, что часы движутся из A в B ,зна­чит они и находятся в движении.

Но если бы Эйнштейн логично поразмыслил, то пришел бы к такому выводу, к какому мы пришли в примере с ав­томобилем. Усомнился бы в вопросе какие часы были в движении и, следовательно, отстанут. Но логическими размышлениями он, как правило, не утруждал себя.

В своих трудах Эйнштейн всегда рассматривал две сис­темы отсчета (координатные системы). Одну из них он считал неподвижной, а другую – движущейся относительно первой (неподвижной). Это могут быть два тела, движущи­еся друг относительно друга. Если бы все на этом и за­канчивалось, то никаких вопросов не возникало бы. Но Эйнштейн на основании такого предположения математиче­ски доказывает, что в движущейся системе размеры в на­правлении скорости уменьшаются, время течет медленнее, масса тела увеличивается.

Опять же, если бы это рассматривалось только как ре­зультат математических упражнений, то и пусть себе бу­дет так. Однако Эйнштейн утверждает, что эти изменения имеют воздействие на реальные физические процессы. Некоторые ученые даже мечтают продлить себе жизнь поле­тав на космическом корабле несколько лет. Там ведь вре­мя течет медленнее.

Но подумать о том, что же будет, если неподвижной считать вторую систему, а первую движущейся, Эйнштейн или не сумел, или, окрыленный победой, не дошел до этого, или подумал, но промолчал. Народ, мол, глуп, и так проглотит. И проглотили.

А ведь понял бы Эйнштейн всю нелепость своих выводов, если бы, предположим, до обеда считал первую систему (первое тело) неподвижной, а вторую (второе тело) дви­жущейся, а после обеда посчитал вторую систему непод­вижной, а первую движущейся.

Но если бы.

ВЫВОД ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА

Рассмотрим как Эйнштейн вывел преобразования Лорен­ца.

Один из вариантов вывода изложен в статье "К элект­родинамике движущихся тел" на стр. 7 и дальше.

Это одна из первых статей Эйнштейна, в которой он попытался теоретически вывести преобразования Лоренца и тем доказать, что это не эмпирические формулы, а формулы, подтвержденные теорией, и следовательно, от­ражающие законы природы.

Чтобы читателю было ясно о чем идет речь, рассмот­рим сначала как он это делал. Вывод преобразований Лоренца изложен в §3 на странице 13 и дальше.

Эйнштейн рассматривает две координатные системы (сис­темы отсчета). Система K неподвижная (покоящаяся) и система k движется относительно неподвижной системы K со скоростью v. Координаты на осях неподвижной сис­темы обозначаются символами х, у, z ивремя сис­темы символом t. В движущейся системе координаты на осях и время обозначаются символами ξ, η, ζ, 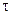. Координатные системы расположены в пространстве так, что соответствующие оси обеих систем всегда остаются взаимно параллельными, а оси x и ξ еще и совпадают. Скорость v направлена вдоль оси х в положительную сто­рону оси.

Обращаем внимание, что в дальнейшем дословные вы­держки из статьи взяты в кавычки. На приведенную ниже выдержку рекомендуем обратить особое внимание. (Стр. 13).

"Представим себе теперь, что пространство размечено как в покоящейся системе K посредством покоящегося в ней масштаба, так и в движущейся системе k посредством движущегося с ней масштаба, и что, таким образом, по­лучены координаты х, у, z и соответственно ξ, η, ζ. Пусть посредством покоящихся часов, находящихся в по­коящейся системе, и с помощью световых сигналов ука­занным в §1 способом определяется время t покоящейся системы для всех тех точек последней, в которых нахо­дятся часы. Пусть далее таким же образом определяется время τдвижущейся системы для всех точек этой систе­мы, в которых находятся покоящиеся относительно пос­ледней часы, указанным в §1 способом световых сигна­лов между точками, в которых эти часы находятся.

Каждому набору значений х, у, z, t,которые пол­нос­тью определяют место и время событий в покоящейся системе, соответствует набор значений ξ, η, ζ, τ, устанавливающий это событие в системе k,и теперь необходимо найти систему уравнений, связывающих эти величины".

Здесь Эйнштейн говорит о том, что каждая из систем ничем не отличается от другой. Для наблюдателя, поко­ящегося в одной системе, все в этой системе выглядит точно так, как и в другой, если он перейдет в эту дру­гую. (Это и есть первый постулат Эйнштейна). Особо об­ращаем внимание на то, что время в каждой системе оди­наковое во всех точках системы. Если бы в каждой точ­ке системы находились часы, то все они шли бы синхрон­но. Значит, время является одним во всей системе, какое в начале системы координат, такое и в бесконечности. Потом Эйнштейн докажет, что это не так, но к тому вре­мени он уже забудет с чего начинал.

Последний абзац говорит о том, что если какая-нибудь произвольно выбранная точка пространства в данный мо­мент имеет координаты x, y, z в одной системе, то в этот же момент та же точка имеет координаты ξ, η, ζ в другой системе. И если в этой точке в этот момент про­изошло какое-нибудь событие, то время, когда произош­ло событие, в одной системе равно t,а в другой .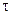

В классической физике все, что здесь сказано, авто­матически воспринимается как должное и не требует осо­бого внимания. Однако в теории относительности боль­шинство авторов или же не поняли то, что написал Эйн­штейн, или же прочитали и тут же забыли о чем там на­писано. По этой причине нигде не упоминают, что коор­динаты обеих систем, связанные преобразованиями Лоре­нца, являются координатами одной и той же точки (такое впечатление, что они об этом и не знают), а пишут, что эти координаты соответствуют друг другу. Как видите, "соответствуют", а не являются координатами одной точки. Вот так, понимай как хочешь.

Дальше Эйнштейн пишет: "Если мы положим 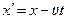,то ясно, что точке, покоящейся в системе k, будет при­надлежать определенный, независимый от времени набор значений x′, y, z ". Надо полагать, что здесь перевод сделан не точно, поэтому приведенная фраза становится понятной только после знакомства с дальнейшим выводом преобразований. Внесем некоторое разъяснение. Эйнштейн произвольно выбрал на общей оси точку (обозначим ее A), которая в движущейся системе k остается неподвижной, а следовательно вместе с этой системой движется со скоростью v относительно неподвижной системы K. Так как точка A в системе k неподвижна, то расстояние от начала координат системы k до точки A всегда остается постоян­ным. Измеряя это расстояние в неподвижной системе K в любой произвольный момент времени, мы также имеем от­резок с постоянной длиной. Эйнштейн обозначил этот отрезок символом х'. Таким образом получается, что в выражении

x является координатой точки А в рассматриваемый момент времени, vt является расстоянием между началами коор­динат систем K и k, и х' является расстоянием от нача­ла координат системы k до точки А. Все эти расстояния определяются в неподвижной системе K.

В результате некоторых математических операций над временем Эйнштейн пришел к следующей зависимости между временем обеих систем

Здесь a –постоянная величина, V –скорость света, а также "принято, что в начале координат системы k при τ = 0 также и t =0 ". Это надо понимать так, что отсчет времени в обеих системах начинается в момент совпаде­ния начал координат систем (расстояние между началами координат ).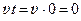

"Для луча света, вышедшего в момент времени τ= 0в направлении возрастающих ξ, имеем

."

Здесь наглядно не видно в какой момент времени выпол­няется эта зависимость. Эйнштейн об этом тоже ничего не сказал. Поэтому при невнимательном чтении создается впечатление, что эта зависимость выполняется в любой момент времени. Но достаточно только рассмотреть эту зависимость в момент времени, когда τ = 0 и t = 0, чтобы стало ясно, что выполняется она не в любой момент вре­мени.

"Но относительно начала координат системы k луч све­та при измерении, произведенном в покоящейся системе, движется со скоростью V – v ,вследствие чего

."

Здесь момент времени t представлен достаточно четко, так как определяется он только постоянными величинами х', V и v .

"Подставив это значение t в уравнение для ξ , получим

".

Дальше Эйнштейн находит

,

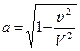подставляет это значение a и в полученные фор­мулы для ξ и τ и получает преобразования Лоренца

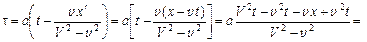
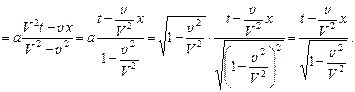
Таким образом, Эйнштейн достиг желаемой цели – полу­чил выведенные теоретически преобразования Лоренца.

Но у наблюдательного читателя сразу возникает вопрос – зачем Эйнштейну понадобилось при выводе преобразова­ния для координат избрать такой более длинный и путан­ный путь? Ведь каждый здраво мыслящий человек в исход­ную формулу 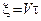подставил бы уже найденное значение 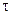и сразу получил бы результат. Эйнштейн очевидно тоже пытался так делать. Но в таком случае получается урав­нение

.

Как видим, это уравнение не похоже на преобразование Лоренца. Это не устраивало Эйнштейна. Ведь в науке на­шли широкое применение преобразования Лоренца, а не это уравнение. Не идти же против течения. Вот и пришлось морочить голову над выводом. То удалять из формулы для τ величину t,то вводить ее снова, пока, наконец, получилось желанное преобразование. Не тогда ли появи­лась, ставшая крылатой, фраза Эйнштейна, что математи­ка – это такая наука, которая любит водить за нос, если нет логической интуиции.

Но если бы у Эйнштейна была логическая интуиция, то он бы увидел, что в полученной им формуле

координата ξ является постоянной величиной, так как определяется только постоянными величинами a, V, v, x′,тогда как в его же формуле

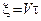
та же координата ξ меняется со временем. Увидел бы и понял, что это несуразица, поэтому нет смысла продолжать дальнейшие математические упражнения. Или, по крайней мере, надо довести решение до конца.

Однако интуиция не появилась.

Эйнштейн не понял, что остановился на полпути и не довел решение до конца. Конечный результат не зависит от способа решения и, при доведенном до конца решении, будет один и тот же. Разберемся, что же должен был по­лучить Эйнштейн в результате своего вывода.

Из используемой Эйнштейном зависимости

следует

С другой стороны, в начале вывода Эйнштейн указал, что

Поскольку в любой момент времени х является координа­той точки А в неподвижной системе, то зависимость выполняется в любой момент времени. Меняются одновременно и координата х и время t, а следователь­но и расстояние vt между началами координат. Иначе обстоит дело из зависимостью

Здесь V – v –величина постоянная. Поэтому 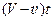с те­че­нием времени меняется и становится равным х' только в один момент

Следовательно, сравнивать этот момент времени с теку­щим временем из можно только в этот момент, т.е. с наложением ограничений на текущее время. Это ог­раничение вытекает из сравнения обоих значений x'.

откуда

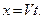
Значит использовать в выводе зависимость можно только при одном условии, что .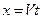

Следовательно, вывод преобразований сделан только для случая, когда свет распространяется вдоль оси x в поло­жительном направлении оси. Дополнительным подтверждением этого является используемая Эйнштейном зависимость

Поскольку по условию х является координатой точки А,то t и 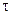означают моменты времени, когда луч света пришел в точку A.

Если бы Эйнштейн логически подумал и не забыл, что согласно с его же утверждением свет в любой системе от­счета распространяется с одной и той же скоростью V, то сразу бы указал, что

и

и не морочил бы голову ни себе, ни другим.

А может быть он и подумал, и не забыл, но схитрил. Ведь надо же было как-то получить преобразования Ло­ренца.

Если бы Эйнштейн знал неоспоримое правило математики, что результат решения любого математического уравнения не зависит от способа решения этого уравнения, и захотел поинтересоваться что получил в результате, то понял бы, что напрасно трудился над разными комбинаци­ями. Результат получается все равно один и тот же, если все доводить до логического конца, а не умышленно отк­лоняться в стороны.

Для примера сделаем вывод преобразований несколькими способами используя зависимости, которые использовал Эйнштейн.

Подставим

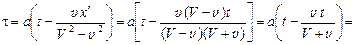
Подставим сначала 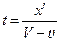, а затем

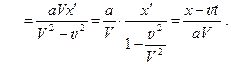
Итак имеем преобразование Лоренца и еще два решения одного и того же уравнения

Напоминаем, что

Поскольку для решения использовались одни и те же величины, то результат во всех трех решениях должен быть одинаков. Таким образом,

Отсюда находим

Так как

то после подстановки и сокращения на V+v получим

Из первого равенства получается

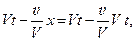
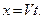
Из второго равенства получается

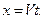
Из третьего равенства получается

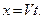
Этот результат мы уже видели, когда сравнивали и .

Эйнштейн нарушал исходные условия, предложенные им же самим и, следовательно, вывел преобразования Лоренца из ничего. Просто манипулируя разными математичес­кими выражениями.

Какие же уравнения должен был получить Эйнштейн, ес­ли бы не нарушал исходные условия и довел решение до конца? Ответ получим, если подставим или 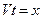в любое,приведенное выше решение.Например,

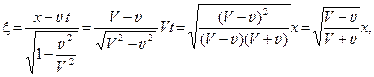
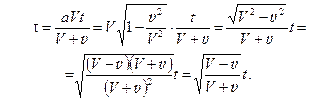
Такие уравнения должен был получить Эйнштейн, если бы не нарушал исходные условия и довел решение до конца. Конечно с обязательным указанием, что (или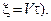

Итак имеем

Как видим, из полученных результатов следует, что по­лученные уравнения распространяются не на всякие про­извольно взятые координаты и промежутки времени, а только на координаты тех точек, до которых дошел свет, и только на те моменты времени, в которые свет дошел до этих точек. При других координатах и других момен­тах времени эти соотношения не выполняются.

Второй вариант вывода преобразований Лоренца Эйн­штейном изложен на стр. 70 и дальше под заглавием "Преоб­разование координат и времени" и повторен на стр.151 и дальше под заглавием "Новые формулы преобразования (преобразование Лоренца) и их физический смысл". Этот вариант наиболее часто встречается и в другой научной литературе. Различия имеются только незначительные и в деталях, не имеющих практического значения. Если не об­ращать внимание на эти различия, то вывод можно изложить, как указано ниже.

Рассматривается движение одной системы отсчета K′со скоростью v относительно другой системы отсчета K, ко­торая считается неподвижной. Оси координат систем па­раллельны, к тому же оси ОХ и O′X′ совпадают. Скорость v направлена вдоль оси ОХ. Координаты и время системы K′ снабжены штрихами, а системы K – без штрихов.

Для преобразования координат и времени при переходе от одной из указанных систем координат к другой Эйнш­тейн выбрал формулы

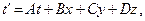
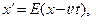
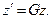
Отсчет времени в этих формулах начинается в момент совпадения начал координат. Дальше Эйнштейн пишет.

"Для определения постоянных A, B, С, D, E, F, G вхо­дящих в уравнения, мы учтем, что в соответствии с при­нципом постоянства скорости света, скорость распрост­ранения имеет одну и ту же величину с по отношению к обеим системам, т.е., что уравнения

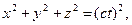
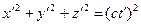
эквивалентны. Заменяя во втором из уравнений t', х', у', z' их значениями и сравнивая с первым уравнением, получаем формулы преобразования".

В результате Эйнштейн получил преобразования Лоренца.

В действительности здесь он должен был получить дру­гие уравнения. Ниже мы покажем почему он должен полу­чить другие уравнения и найдем эти уравнения.

Уравнения

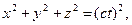
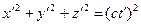
Эйнштейн считал уравнениями сферы, которая представля­ет собой фронт волны света, испущенного из начала ко­ординат в момент совпадения начал координат обеих сис­тем. Некоторые ученые даже считают, что это две сферы. По одной сфере в каждой системе.

В действительности эти уравнения не являются уравне­ниями одной и другой сферы. Если считать, что имеем дело с двумя сферами, то надо не забывать, что эти сфе­ры имеют разные центры, которые являются началами ко­ординат в разных системах. Следовательно, сферы разне­сены в пространстве, и ни одна точка одной сферы не совпадает с точкой другой сферы (кроме, конечно, точек пересечения). А это значит, что уравнения не только не эквивалентные в этом случае, а и вообще ничем не свя­заны между собой, а следовательно и координаты, входя­щие в уравнения, ничем не связаны между собой.

Если считать, что это одна и та же сфера, но с двумя центрами, тогда ct и ct' не могут быть радиусами, так как их длина будет зависеть от направления их в пространс­тве. Например, для луча, который распространяется вдоль оси OX в положительном направлении, ct = x и ct′ = x′. В этом направлении х' меньше, чем х,значит и радиус ct' меньше, чем сt. А для луча, который распространяется в отрицательном направлении, абсолютная величина х' боль­ше, чем х, значит радиус ct' больше, чем сt. Чтобы яс­нее это все представить, давайте посчитаем, что радиус ct не зависит от направления и остается постоянным. Тогда ясно видно, что радиус ct' то больше, то меньше ct в зависимости от направления. Следовательно, ct' в дан­ном случае не может быть радиусом. Неодновременность событий здесь не поможет. С ней мы разберемся позже. Из сказанного становится ясно, что рассматриваемые уравне­ния не являются уравнениями сферы.

Чтобы не было недоразумений, надо четко определиться в понимании значения уравнения типа

Так вот, это уравнение в общем случае является уравне­нием точки, произвольно выбранной в пространстве, неза­висимо от того, где находится эта точка. Точка может находиться и насфере, и на стороне прямоугольного объекта, и на любой кривой или прямой линии, располо­женной в пространстве, или просто является точечным объектом. В этом уравнении х, у, z есть координаты этой точки, а R – расстояние от начала координат до этой точки.

И только в частном случае, когда имеем много точек, и все они находятся на одинаковом расстоянии от начала координат, эти много точек вместе взятые представляют собой сферу, а расстояние R от начала координат до лю­бой из этих точек одинаково. Таким образом, применить указанное уравнение к сфере можно только в том случае, когда расстояние R остается постоянным при любом нап­равлении в пространстве. В этом случае R является радиусом сферы. Если же мы имеем объект, точки которого находятся на разных расстояниях от начала координат, то это может быть какая угодно другая поверхность, в том числе и сфера, но у этой сферы R не будет уже радиусом, а начало координат не будет центром.

Таким образом, уравнения

не просто эквивалентные, как пишет Эйнштейн, а являются уравнениями одной и той же точки. В неподвижной систе­ме координатами этой точки являются х, у, z, a ct является расстоянием от начала координат до этой точки. В движущейся системе координатами этой точки являются x', y', z' ирасстоянием является ct'. Расстояния ct и ct' указывают на то, что точка эта выбрана в тот мо­мент времени, когда свет пришел в эту точку.

В результате надо заключить, что эти уравнения явля­ются уравнениями одной и той же точки, произвольно вы­бранной в пространстве в момент времени, когда в эту точку пришел фронт волны света (т.е. начало луча све­та). Наглядно это изображено на рис. 1.

Чтобы не загромождать рисунок, точка P выбрана в прос­транстве на координатной плоскости ХОY . В этом случае координаты z и z' равны нулю. На рисунке x и у –коор­динаты точки Р в неподвижной системе K, х' и y′–

коор­динаты точки Р в движущейся системе K', ct и ct' –расс­тояния, пройденные лучами света в той и другой систе­мах от момента вспышки до момента достижения точки Р. ОО' –расстояние, на которое передвинулась движущаяся система относительно неподвижной за время, пока луч дошел до точки Р. Точка F –проекция точки Р на общую ось OХ (O′X′).

Поскольку в случае, представленном на рис. 1, z и z' равны нулю, то уравнения для точки Р перепишутся в следующем виде

Оси ОХ и O′X′ совпадают. Следовательно, они представляют собой одну прямую линию. Тогда расстояние PF от этих осей до точки Р одинаковое в обеих системах. Это расстояние является координатой у и у'. Значит

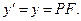
Решим уравнения относительно y и у'.

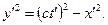
Это означает, что

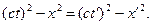
Эта зависимость легко получается и из рис. 1 без из­лишних доводов. На рисунке представлено два прямоуголь­ных треугольника OPF и O'PF у которых PF общий катет. В соответствии с теоремой Пифагора в прямоугольном тре­угольнике сумма квадратов катетов равна квадрату гипо­тенузы. Из этого следует, что квадрат катета равен квадрату гипотенузы минус квадрат другого катета. Катет PF общий, поэтому получится из любого треугольника, о чем и записано в уравнении.

В этом уравнении, как видим, речь не идет о каком-то времени одной и другой системы. Речь идет здесь о сто­ронах одного и другого треугольника, а это отрезки прямой. С течением времени и луч перейдет в другую точ­ку, и движущаяся система переместится. Следовательно, по­меняются размеры треугольников, однако взаимоотноше­ния между их сторонами не поменяются. Поэтому выполнен­ная Эйнштейном задача – это не определение пространственно-временных соотношений, а определение взаимоотно­шений между сторонами указанных треугольников.

Используем замену, подобную предложенной Эйнштейном.

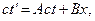
Подставим эти значения в наше уравнение

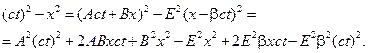Чтобы это выполнялось, надо чтобы в правой части получилось такое же выражение, как и в левой. А для этого надо, чтобы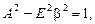

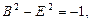
Решив эту систему уравнений, найдем

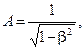
Таким образом, решением будет

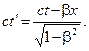
Как видим, получились уравнения, в которых указано соотношение между линейными величинами х, x', ct, ct',которые заданы и в исходных уравнениях. Непривычным здесь является то, что расстояния от начала координат до точки Р выражены произведением двух величин. Однако это расстояния, т.е. линейные величины.

На рис. 1 мы видим, что ct' меньше ct. Разумеется, это так и должно быть при том расположении систем и точки Р,которые представлено на рисунке. А раз ct' меньше ct, то естественно, что второй сомножитель t′должен быть меньше второго сомножителя t,так как первый сомножитель с одинаков в обоих произведениях. Эйнштейн это истолковывает будто время в движущейся системе течет медленнее, потому и t' меньше t. Мы же видим, что расстояние ct' меньше, чем сt. А поскольку эти расстояния свет проходил с одинаковой скоростью, то и времени ему потребовалось для прохождения рассто­яния сt′ меньше, чем для прохождения расстояния сt. Ес­ли бы Эйнштейн мог и захотел логически мыслить, он бы тоже пришел к этому результату. Но, если бы.

Как же получилось, что Эйнштейн получил преобразова­ния Лоренца? Все объясняется просто. Эйнштейн производил решение относительно х, х', t, t',вместо x, x', ct, ct′. Поэтому в процессе решения получилось авто­матически сокращение на с, и поэтому получились пре­образования Лоренца. Если мы полученные нами уравнения сократим на с, они тоже превратятся в преобразования Лоренца. Но наше решение отличается четким указанием на то, что t и t' не являются временем той и другой си­стемы, а являются промежутками времени, затраченными лучами на прохождение расстояний ct и сt'. Разумеется, каждому должно быть известно, что после сокращения или любого другого преобразования уравнения значение его членов не меняется. Поэтому и после сокращения на с, т.е. в преобразованиях Лоренца t и t′ не стали време­нем той и другой системы.

Третий вариант вывода преобразований Лоренца Эйн­штейном изложен на странице 588 и дальше под заглавием "Простой вывод преобразований Лоренца".

В этом выводе Эйнштейном рассматриваются две коорди­натные системы K и K'. Система K' движется относительно системы K вдоль оси ОХ в положительном направлении. Оси систем взаимно параллельны, причем оси ОХ и O'Х' совпа­дают. Координаты и время системы K′ снабжены штрихами, а системы K –без штрихов.

Чтобы читателю было ясно, о чем идет речь, кратко из­ложим материал так, как излагал его Эйнштейн.

"Световой сигнал, распространяющийся в положительном направлении оси X,движется в соответствии с уравне­нием

или

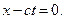(1)

Так как этот же световой сигнал распространяется и от­носительно K' с той же скоростью с,то его движение относительно системы K' будет описываться уравнением

(2)

Пространственно-временные точки (события), удовлетво­ряющие уравнению (l), должны удовлетворять также урав­нению (2). Это, очевидно, будет иметь место в том слу­чае, если вообще выполняется соотношение

(3)

где λ – некоторая постоянная. В самом деле, согласно соотношению (3) обращение в нуль выражения 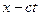озна­чает обращение в нуль и .

Совершенно аналогичное рассуждение, примененное к световым лучам, распространяющимся в отрицательном на­правлении оси X , приводит к условию

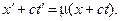(4)

Складывая и вычитая соотношения (3) и (4) и при этом вводя для удобства вместо постоянных λ и 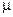новые пос­тоянные

получаем

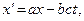
(5)''

Дальше пошли алгебраические преобразования, которые и превратили (5) в преобразования Лоренца.

Поскольку Эйнштейном указаны не все промежуточные преобразования, то читатель может и не понять как все получилось. Поэтому покажем все преобразования подроб­но.

Полученное уравнение

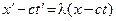
у каждого здраво мыслящего человека должно вызвать не­доумение. Ведь 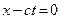(как и )получено из уравнения x = ct,следовательно x – ct = ct – ct = 0всегда равно нулю, при любом t и при любом x. Меняется t – ме­няется и х и, с другой стороны, х всегда равен сt. Поэтому x – ct всегда равно нулю. Аналогично и x' – ct' всегда равно нулю. Таким образом, уравнение, которое составил Эйнштейн, можно записать в следующем виде

Оно выполняется при любом значении λ.

Но Эйнштейн же что-то думал, когда составлял это уравнение. Представим себе, что он считал х и ct как две независимые величины, ничем не связанные друг с другом. Если значение х увеличилось, например, в два раза, то значение ct может и не измениться, или тоже уве­­личилось, но только, например, в пять раз, и т.д. А x = ct – это только случайное совпадение. Тогда неясно, как это получилось, что одн

Читайте також:

1. ГЛАВА 10. ФИЛОСОФИЯ Г.В.Ф. ГЕГЕЛЯ. НАУКА ЛОГИКИ. УЧЕНИЕ О СУЩНОСТИ
2. КОНЦЕПЦИЯ ЛОГИКИ
3. Тема 1. Предмет и значение логики

Переглядів: 581