• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Мета роботи: вивчити способи переводу чисел з однієї системи числення в іншу та представлення від'ємних і дробових чисел у пам'яті комп'ютера.

Теоретичні відомості

Сукупність прийомів та правил найменування й позначення чисел називається системою числення. Основою системи числення називається число, яке означає, у скільки разів одиниця наступного розряду більше за одиницю попереднього.

Дискретне повідомлення містить набір чисел і символів. Кожне число містить цифри. Утворення чисел у будь-якій системі числення проводять таким чином: фіксують позиції, що називаються розрядами, кожному розряду присвоюють свою вагу h_і (де і – номер розряду); h_i=pⁱ (p — основа системи); в розрядах розміщують цифри а_і. Тоді будь-яке число А можна подати у вигляді:

,

де n – число знаків до коми; m – число знаків після коми. Послідовність цифр

a_n-1, a_n-2,....., a₁, a₀, a_-1, a_-2,......, a_-m

можна розглядати як код числа в заданій системі числення.

Система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється, називається непозиційною. У цифровій техніці використовуються так звані позиційні системи числення. Система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа, називається позиційною.

У непозиційній системі кожен знак у запису незалежно від місця означає одне й те саме число. Добре відомим прикладом непозиційної системи числення є римська система, в якій роль цифр відіграють букви алфавіту: І — один, V — п'ять, Х — десять, С — сто, Z — п'ятдесят, D — п'ятсот, М — тисяча.

Наприклад, 324 = СССХХІV. У непозиційній системі числення незручно й складно виконувати арифметичні операції.

Основою позиційної системи числення є число десять. Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад:

130678 = 1*10⁵+3*10⁴+0*10³+6*10²+7*10¹+8.

Тут 10 є основою системи числення, а показник степеня — це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел, для яких необхідним є знання таблиці додавання.

У процесі налагодження програм та в деяких інших ситуаціях у програмуванні актуальною є проблема переведення чисел з однієї позиційної системи числення в іншу. Проблема вибору системи числення для подання чисел у пам'яті комп'ютера має велике практичне значення. В разі її вибору звичайно враховуються такі вимоги, як надійність подання чисел при використанні фізичних елементів, економічність (використання таких систем числення, в яких кількість елементів для подання чисел із деякого діапазону була б мінімальною).

Якщо основа нової системи числення дорівнює деякому степеню старої системи числення, то алгоритм переводу дуже простий: потрібно згрупувати справа наліво розряди в кількості, що дорівнює показнику степеня і замінити цю групу розрядів відповідним символом нової системи числення. Цим алгоритмом зручно користуватися, коли потрібно перевести число з двійкової системи числення у вісімкову або шістнадцяткову.

Наприклад, 10110₂=10110=26₈, 1011100₂=1011100=5C₈

У двійковому відбувається за зворотнім правилом: один символ старої системи числення заміняється групою розрядів нової системи числення, в кількості рівній показнику степеня нової системи числення.

Наприклад, 472₈=100111010=100111010₂, B516=10110101=10110101₂

У цифровій техніці найпоширенішою для подання чисел у пам'яті комп'ютера є двійкова система числення. Для зображення чисел у цій системі необхідно дві цифри: 0 і 1, тобто достатньо двох стійких станів фізичних елементів. Наприклад, число 25.5 в десятковій і двійковій системах числення може бути подане у вигляді

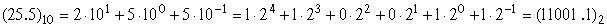
Значно рідше використовують вісімкову і шістнадцяткову системи. Їх застосовують при складанні програм для більш зручного та короткого запису двійкових кодів команд, бо ці системи не вимагають спеціальних операцій для переведення в двійкову систему.

1. Правила виконання арифметичних дій над двійковими числами

Додавання	Віднімання	Множення	Додавання за mod 2
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10	0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 - 1 = 1	0*0 = 0 0*1 = 0 1*0 = 0 1*1 = 1	0 0 = 0 0 1 = 1 1 0 = 1 1 1 = 0

Оскільки 2³ = 8, а 2⁴ = 16, то кожних три двійкових розряди зображення числа утворюють один вісімковий, а кожних чотири двійкових розряди — один шістнадцятковий. Тому для скорочення запису адрес та вмісту оперативної пам'яті комп'ютера використовують шістнадцяткову й вісімкову системи числення.

Основа однієї системи числення дорівнює деякому степеню іншої. У протилежному випадкові користуються правилами переведення числа з однієї позиційної системи числення в іншу (найчастіше для переведення із 2-ї, 8-ї та 16-ї систем числення у 10-у і навпаки).

Переглядів: 633