
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Моменти сили відносно центра (точки)
При розгляданні просторової системи сил, прикладених до твердого тіла, обертальна дія сили визначається її векторним моментом відносно точки, а при розгляданні системи сил що лежать у одній площині, обертальна дія сили визначається її алгебраїчним моментом відносно точки.
 Задана сила
Задана сила  , зображено вектором
, зображено вектором  , прикладена до деякого тіла в точці А . Визначимо моменти сили
, прикладена до деякого тіла в точці А . Визначимо моменти сили  відносно центра О (рис. 3.1).
відносно центра О (рис. 3.1).
а). Векторний момент сили відносно точки (центра).
Векторним моментом сили відносно точки (центра) називається вектор, прикладений в центрі О , який дорівнює векторному добутку радіуса-вектора точки прикладання сили на вектор сили.
 (3.1) де
(3.1) де 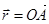 - радіус-вектор точки прикладання сили відносно центра О .
- радіус-вектор точки прикладання сили відносно центра О .
Визначимо величину (модуль) напрямлення вектора  . Згідно з поняттям і властивостями векторного добутку двох векторів величина (модуль) векторного момента сили відносно центра.
. Згідно з поняттям і властивостями векторного добутку двох векторів величина (модуль) векторного момента сили відносно центра.
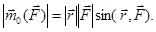 (3.2)
(3.2)
Позначимо кут (  ) = β , а
) = β , а 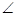 ОАВ = α. Оскільки
ОАВ = α. Оскільки 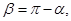 а
а 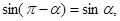 тоді
тоді
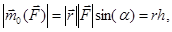 (3.3)
(3.3)
де  (рис. 3.1) – висота ΔОАВ, опущена з вершини О (з центра О ) на сторону АВ цього трикутника, що збігається з лінією дії сили.
(рис. 3.1) – висота ΔОАВ, опущена з вершини О (з центра О ) на сторону АВ цього трикутника, що збігається з лінією дії сили.
Відстань від центра О до лінії дії сили називається плечем сили відносно цього центра і визначається буквою h (рис. 3.1).
Таким чином, модуль (величина) моменту сили відносно центра дорівнює добутку величини сили на її плече відносно цього центра.
Вектор 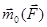 спрямовується за правилом векторного добутку; тобто векторний момент сили відносно центра (точки) спрямовано перпендикулярно до площини, в якій розміщенні сили і центр так, щоб з його кінця було видно намагання сили повертати тіло навколо центра проти ходу стрілки годинника (рис. 3.1).
спрямовується за правилом векторного добутку; тобто векторний момент сили відносно центра (точки) спрямовано перпендикулярно до площини, в якій розміщенні сили і центр так, щоб з його кінця було видно намагання сили повертати тіло навколо центра проти ходу стрілки годинника (рис. 3.1).
Зауважимо, що 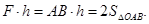 Тому
Тому 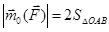 . Отже, модуль векторного момента сили відносно центра дорівнює подвоєній площі трикутника, побудованого на вектора
. Отже, модуль векторного момента сили відносно центра дорівнює подвоєній площі трикутника, побудованого на вектора  і
і  .
.
Якщо лінія дії сили проходить через центр (точку) то, як видно з рис. 3.1 і формули (2.2), момент сили відносно цього центра буде дорівнювати нулю, тому що немає плеча.
Момент сили відносно точки не змінюється при перенесенні сили вздовж її лінії дій, оскільки незмінним залишається плече сили відносно центра (рис. 3.1).
б). Алгебраїчний момент сили відносно точки (центра).
Якщо на тіло діє плоска система сил, то вектори моментів всіх сил системи відносно деякого центра, що лежить в площині дії сил, будуть перпендикулярні до цієї площині, і отже, паралельні. Тому моменти будуть додаватися алгебраїчно і їх можна вважати скалярними величинами, які відрізняються лише величиною та знаками. Отже, в цьому випадку доцільно ввести поняття алгебраїчного моменту сили відносно точки.
Алгебраїчним моментом сили відносно центра (точки) називається взятий зі знаком плюс, або мінус, добуток модуля сили на її плече відносно цієї точки:
 (3.4)
(3.4)
 Вважатимемо алгебраїчний момент додатним, якщо сила намагається обертати тіло відносно центра (точки) проти ходу стрілки годинника (рис.3.2, а) і від’ємним – якщо за ходом стрілки годинника (рис. 3.2, б). Одиниця моменту сили:1 Н*м.
Вважатимемо алгебраїчний момент додатним, якщо сила намагається обертати тіло відносно центра (точки) проти ходу стрілки годинника (рис.3.2, а) і від’ємним – якщо за ходом стрілки годинника (рис. 3.2, б). Одиниця моменту сили:1 Н*м.
Читайте також:
- III. центральная нервная система
- IV. Система зв’язків всередині центральної нервової системи
- А джерелами фінансування державні капітальні вкладення поділяються на централізовані та децентралізовані.
- Аборт как центральная проблема биоэтики
- Активні операції центральних банків.
- Аналіз витрат за центрами відповідальності.
- АНАТОМІЯ І ФІЗІОЛОГІЯ ЦЕНТРАЛЬНОЇ ТА ПЕРИФЕРИЧНОЇ НЕРВОВОЇ СИСТЕМИ, ЇЇ ВІКОВІ ОСОБЛИВОСТІ
- Антиукраїнська політика російського царизму. Посилення централізаторсько-шовіністичних тенденцій
- Архіви центральних установ Великого князівства Литовського та Речі Посполитої. Литовська та Коронна метрики. Волинська метрика
- Асортиментний процес включає три основних етапи: концентрацію, кастомізацію і розсіювання.
- Банківська система в ринковій економіці є звичайно дворівневою і включає центральний банк (емісійний) і комерційні (депозитні) банки різних видів.
- Банківська система та її структура. Функції Центрального банку.
| <== попередня сторінка | | | наступна сторінка ==> |
| Статично означені і статично неозначені задачі статики | | | Момент сили відносно осі |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |