Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв'язання

Інформаційні втрати в каналі зв'язку визначаються умовною ентропією H(X/Y) одного джерела щодо іншого.

Для того щоб обчислити повну умовну ентропію H(X/Y), потрібно знайти розподіли безумовних ймовірностей p(x_i), p(y_j) і побудувати матрицю умовних ймовірностей p(x_i/y_j).

Безумовний закон розподілу p(x_i) знаходимо, виконавши в матриці сумісних ймовірностей p(x_i, y_j) згортку за j:

p(x₁)= 0,15+0,15+0=0,3, i=1;

p(x₂)= 0+0,25+0,1=0,35, i=2;

p(x₃)= 0+0,2+0,15=0,35, i=3.

Перевіряємо умову нормування

p(x₁)+ p(x₂)+ p(x₃)=0,3+0,35+0,35=1.

Виходячи з розподілу безумовних ймовірностей д. в. в. X, обчислимо її ентропію:

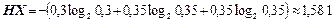(біт/сим).

Безумовний закон розподілу p(y_j) знаходимо, виконавши в матриці сумісних ймовірностей p(x_i, y_j) згортку за i:

p(y₁)= 0,15+0+0=0,15, j=1;

p(y₂)= 0,15+0,25+0,2=0,6, j=2;

p(y₃)= 0+0,1+0,15=0,25, j=3.

Перевіряємо умову нормування:

p(y₁)+ p(y₂)+ p(y₃)=0,15+0,6+0,25=1.

Матрицю умовних ймовірностей знаходимо, скориставшись формулою множення ймовірностей p(x_i, y_j)=p(y_j)×p(x_i/y_j).

Звідси випливає, що .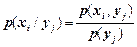

Отже, матриця умовних ймовірностей p(x_i/y_j) знаходиться так:

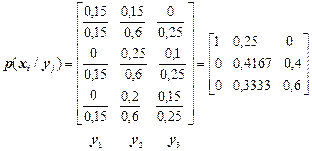Для матриціумовних ймовірностей p(x_i/y_j) повинна виконуватися умова нормування

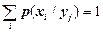Перевіряємо цю умову:

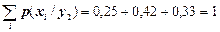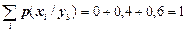Скориставшись матрицею умовний ймовірностей p(x_i/y_j), обчислимо часткові умовні ентропії Xстосовно Y:

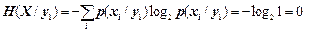(біт/сим);

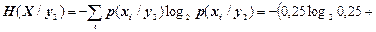
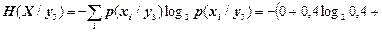
(біт/сим).

Виходячи з безумовного закону розподілу д. в. в. Y та знайдених часткових умовних ентропій H(X/y_j), відшукуємо їх математичне сподівання – загальну умовну ентропію

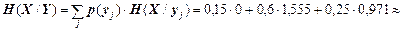
(біт/сим).Отже, інформаційні втрати в каналі зв'язку H(X/Y)»1,18 (біт/сим).

Пропускна здатністьканалу із шумом обчислюється за формулою

де через k позначено об'єм алфавіту джерела; t - час вибору повідомлення джерелом.

Отже, отримаємо 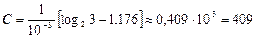(бод).

Кількість переданої по каналу інформації,що припадає на одне повідомлення джерела, знаходиться, виходячи із середньої кількості інформації, що виробляється джерелом – його ентропії і інформаційних втрат в каналі:

I(X, Y)=HX-H(X/Y)=1,581-1,176»0,406 (біт/сим).

Швидкість передачі інформації знаходиться так:

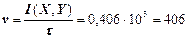(бод).

Відповідь: H(X/Y)»1,18 (біт/сим); C»409 (бод); v=406 (бод).

Задачі до розділу 2

1Дослідження каналу зв'язку між джерелом X і спостерігачем Y виявило такі умовні ймовірності вибору повідомлень y_jÎY:

Знайти часткові H(X/y_j) і загальну H(X/Y) умовні ентропії повідомлень у цьому каналі, якщо джерело задане ансамблем {x₁, x₂, x₃} з ймовірностями {0,3; 0,2; 0,5}.

2Два статистично залежних джерела X та Y визначаються матрицею сумісних ймовірностей

Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і взаємну інформацію I(X, Y).

3Два статистично залежних джерела Xта Y визначаються матрицею сумісних ймовірностей

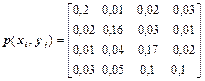Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і взаємну інформацію I(X, Y).

4Матриця сумісних ймовірностей каналу зв'язку має вигляд

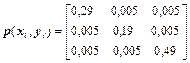Знайти часткові й загальну умовні ентропії H(X/y_j), H(X/Y) і взаємну інформацію I(X, Y).

5Дослідження каналу зв'язку між джерелом X і спостерігачем Y виявило такі умовні ймовірності вибору повідомлень y_jÎY:

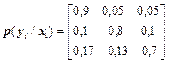Знайти часткові й загальну умовні ентропії повідомлень у цьому каналі H(X/y_j), H(X/Y), якщо джерело задане ансамблем {x₁, x₂, x₃} з ймовірностями {0,7; 0,2; 0,1}.

6Джерело повідомлень X задано ансамблем {x₁, x₂, x₃} з ймовірностями p(x₁)=0,65, p(x₂)=0,25, p(x₃)=0,1. Матриця умовних ймовірностей каналу має вигляд

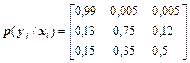Знайти кількість інформації, передану в одному й 100 повідомленнях джерела, інформаційні втрати в каналі при передачі 100 повідомлень з алфавіту X?

7Канал передачі інформації заданий ансамблем {x₁, x₂, x₃} з ймовірностями {0,3; 0,2; 0,5}. Матриця умовних ймовірностей каналу має вигляд

Знайти інформаційні втрати в каналі, пропускну здатність каналу й швидкість передачі повідомлень джерелом, якщо час передачі одного повідомлення t=10^-3 c.

8Матриця сумісних ймовірностей каналу зв'язку має вигляд

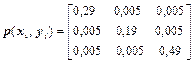Знайти інформаційні втрати в каналі й швидкість передачі інформації, якщо час передачі одного повідомлення t=10^-3 c.

9Знайти кількість переданої інформації в одному повідомленні джерела й пропускну здатність каналу зв'язку при t=10^-3c, де t - час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд

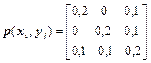10Знайти пропускну здатність каналу зв'язку при t=10^-2c, де t - час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд

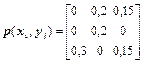Чи можлива безпомилкова передача в цьому каналі, якщо продуктивність джерела V_дж=96 сим/с?

11Знайти інформаційні втрати в каналі й пропускну здатність дискретного каналу зв'язку при t=10^-3 c, де t- час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд

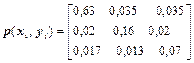Чи можлива безпомилкова передача інформації в цьому каналі, якщо продуктивність джерела V_дж=860 сим/с?

Контрольні запитання до розділів 1-2

1 Які існують види інформації?

2 Як перевести неперервну інформацію в дискретний (цифровий) вигляд?

3 Що таке частота дискретизації неперервної інформації?

4 Як формулюється теорема дискретизації?

5 Що таке інформація, кодування, канал зв'язку, шум?

6 У чому полягають основні положення Шеннона до визначення кількості інформації?

7 Як визначається кількість інформації, що міститься в одному повідомленні дискретного джерела?

8 Як визначається кількість інформації на одне повідомлення джерела взаємозалежних повідомлень?

9 Що таке ентропія джерела? Які її властивості?

10 За яких умов ентропія джерела максимальна?

11 Як визначається кількість інформації? Які властивості кількості інформації?

12 Що таке умовна ентропія?

13 Як описується модель системи передачі інформації?

14 Які є види умовної ентропії?

15 Які основні властивості умовної ентропії?

16 Як знаходиться часткова умовна ентропія?

17 Як знаходиться загальна умовна ентропія?

18 Чим обумовлена статистична надмірність джерела інформації?

19 Чим визначається ентропія об'єднання двох джерел інформації?

20 Які основні властивості взаємної ентропії?

21 Як знаходиться кількість інформації на одне повідомлення двох статистично залежних джерел?

22 Що таке продуктивність джерела інформації?

23 Як визначається швидкість передачі інформації по каналу зв'язку?

24 Чим визначаються інформаційні втрати при передачі інформації по каналу зв'язку?

25 Чим визначаються інформаційні втрати в каналі за відсутності завад?

26 Чим визначаються інформаційні втрати в каналі при великому рівні завад?

27 Чим визначаються інформаційні втрати в каналі за наявності завад?

28 Як знаходиться кількість інформації, передана в одному повідомленні?

29 Чим визначається пропускна спроможність каналу зв'язку?

30 Чим визначається пропускна спроможність каналу зв'язку за відсутності завад?

31 Як формулюється теорема Шеннона про кодування дискретного джерела за відсутності завад?

32 Як формулюється теорема Шеннона про кодування дискретного джерела за наявності завад?

33 Як формулюється зворотна теорема Фано про кодування дискретного джерела за наявності завад?

Частина II Економне кодування інформації. Статистичні та словникові методи стиснення даних

Розділ 3 ОПТИМАЛЬНІ СТАТИСТИЧНІ МЕТОДИ СТИСНЕННЯ ІНФОРМАЦІЇ

3.1 Способи задання кодів. Статистичне кодування

Кодування інформації, здійснюване для зменшення надмірності повідомлень, називається економним кодуванням, або стисненням інформації.

Мета стиснення - зменшення кількості бітів, необхідних для зберігання і передачі інформації, що надає можливість передавати повідомлення швидше і зберігати економніше і оперативніше.

Розглянемо приклади кодів і способи їх задання.

Найпростішим способом представлення кодів є кодові таблиці, що зіставляють символам повідомлень певні кодові комбінації. Приклад кодової таблиці подається в табл. 2.1.

Неважко переконатися, що будь-яке повідомлення x_i з алфавіту об'ємом k можна закодувати послідовністю кодових символів з набору розміром N=q^l комбінацій, де N³k, l - довжина кодової комбінації. У загальному випадку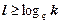. Наприклад: k=32, q=2, тоді l=5, відповідними двійковими кодовими комбінаціями будуть 00000…11111; k=1000, q=10, тоді l=3, кодові комбінації – 0…999.

Основа коду q може бути довільною, проте в комп'ютерних системах передачі і зберігання інформації найбільш поширені двійкові (бінарні) коди.

Таблиця 2.1

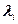
Символ x_i Число Код з основою 10 Код з основою 4 Код з основою 2

А

Б

В

Г

Д

Е

Ж

З

Наочним і зручним способом задання кодів є їхнє подання у виглядікодового дерева(рис. 2.1).

Рисунок 2. 1

Для цього, починаючи з деякої точки - кореня кодового дерева, проводяться гілки, що позначаються 0 або 1. На листях кодового дерева знаходяться символи алфавіту джерела, причому кожному символу відповідає свій лист і свій шлях від кореня до відповідного листа, який утворює певну кодову комбінацію.

Код, поданий кодовим деревом на рис. 2.1, є примітивним рівномірнимтрирозрядним кодом. Перевага рівномірних кодів, що мають однакову для всіх символів довжину, полягає в простоті кодування/декодування і синхронізації системи (рис. 2.2).

Прикладом нерівномірного коду може бути кодове дерево, зображене на рис. 2.3.

Рисунок 2. 3

Це приклад непрефіксних кодів. На практиці такі коди не можуть застосовуватися без спеціальних роздільників.

Найбільш поширені нерівномірні коди, що однозначно декодуються. Для цього необхідно, щоб всім символам алфавіту відповідали листя кодового дерева (рис. 2.4), причому жодна кодова комбінація не повинна бути початком (префіксом) іншої, більш довгої, - це префіксні коди.

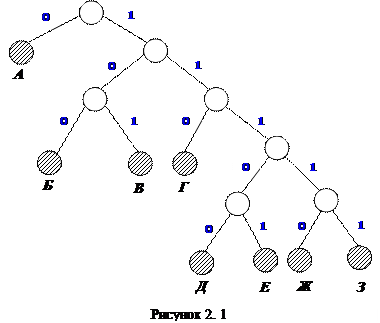
Задача прийому і декодування нерівномірних кодів набагато складніша, оскільки надходження елементів повідомлення стає неперіодичним (рис.2.5).

Розглянемо приклади кодування повідомлень x_i з алфавіту об'ємом k=8 за допомогою l-розрядного двійкового коду.

Приклад 1 Нехай джерело видає одне з 8 повідомлень А...З, що мають однакову імовірність.

Кодування цих повідомлень рівномірним трирозрядним кодом наведено в табл. 2.1. Тоді:

- ентропія джерела 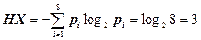(біт/сим);

- надлишковість джерела ;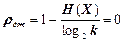

- середня довжина коду 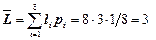(біт/сим);

- надлишковість коду .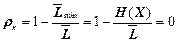

Отже, при передачі рівноімовірних повідомлень надлишковість рівномірного коду дорівнює нулю, тобто в цьому випадку рівномірне кодування є оптимальним.

Приклад 2 Припустимо, що повідомлення нерівноймовірні (табл. 2.2).

Таблиця 2.2

А Б В Г Д Е Ж З

0,6 0,2 0,1 0,04 0,025 0,015 0,01 0,01

Ентропія джерела при цьому буде менше: Н(Х)»1,781 (біт/сим).

Середнє число символів на одне повідомлення при використовуванні рівномірного трирозрядного коду 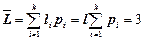(біт/сим).

Надлишковість коду 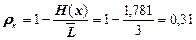, тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).

Отже, при кодуванні нерівноімовірних повідомлень рівномірні коди характеризуються значною надмірністю. У таких випадках доцільно використовувати нерівномірні коди, довжина кодових комбінацій яких залежить від імовірності символів в повідомленні. Таке кодування називається статистичним.Нерівномірний код при статистичному кодуванні вибирається так, щоб більш імовірні значення передавалися за допомогою більш коротких комбінацій коду, а менш імовірні - за допомогою більш довгих. У результаті зменшується середня довжина коду.

3.2 Елементи теорії префіксних множин

Префіксною множиноюS називається скінченна множина двійкових слів, в якій жодна з послідовностей не є префіксом (початком) ніякої іншої.

Якщо S={w₁, w₂, …, w_k} – префіксна множина, то можна визначити вектор n(S)=(L₁, L₂, …, L_k), що складається із значень довжин відповідних префіксних послідовностей у неспадному порядку. Цей вектор називається вектором Крафта,для якого виконується нерівність Крафта:

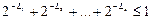. (2.1)

Для вектора Крафта справедливе таке твердження: якщо S - префіксна множина, то n(S) - вектор Крафта.

Якщо нерівність (2.1) переходить в строгу рівність, то такий код називається компактнимі має найменшу серед кодів з даним алфавітом довжину, тобто є оптимальним.

Приклади префіксних множин і відповідних їм векторів Крафта: S1={0, 10, 11}® n(S1)=(1, 2, 2); S2={0, 10, 110, 111}® n(S2)=(1, 2, 3, 3); S3={0, 10, 110, 1110, 1111}® n(S3)=(1, 2, 3, 4, 4); S4={0, 10, 1100, 1101, 1110, 1111}® n(S4)={1, 2, 4, 4, 4, 4}; S5={0, 10, 1100, 1101, 1110, 11110, 11111}® n(S5)=(1, 2, 4, 4, 4, 5, 5); S6={0, 10, 1100, 1101, 1110, 11110, 111110, 111111}® n(S6)=(1, 2, 4, 4, 4, 5, 6, 6).

Припустимо, використовується код без пам'яті для стиснення вектора даних x=(x₁, x₂, …, x_n) з алфавітом А об'ємом k символів.

Позначимо через F=(F₁, F₂, …, F_k) вектор частот символів алфавіту А в повідомленні X.

Кодування повідомлення кодом без пам'яті здійснюється у такий спосіб:

1) складається список символів алфавіту A: a₁, a₂, …, a_k у порядку спадання їх частот появи в X;

2) кожному символу а_jпризначається кодове слово w_j з префіксної множини S двійкових послідовностей, для якої вектор Крафта n(S)=(L₁, L₂, …, L_k);

3) виходом кодера є об'єднання в одну послідовність усіх отриманих кодових слів.

Тоді довжина кодової послідовності на виході кодера джерела інформації становить

L(X)=L×F=L₁×F₁+ L₂×F₂+…+ L_k×F_k. (2.2)

Оптимальним є префіксний код, для якого добуток L×F мінімальний: L×F® min.

3.3 Оптимальні методи статистичного стиснення інформації Шеннона-Фано і Хаффмена

До оптимальних методів статистичного кодування повідомлень належать алгоритми Шеннона-Фано і Хаффмана. Ці алгоритми є найпростішими методами стиснення інформації і належать до так званих кодів без пам'яті(біт/сим).

Обчислимо середню довжину оптимальних кодів Шеннона-Фано і Хаффмена для кодування даної д. в. в.

I Метод Шеннона-Фано:

Побудуємо таблицю кодів Шеннона-Фано (табл. 1):

Таблиця 1

Імовірність p_i Код Code(x_i) Довжина коду l_i p_il_i

0,18 0,36

0,17 0,51

0,16 0,48

0,15 0,45

0,1 0,3

0,08 0,32

0,05 0,2

0,05 0,2

0,04 0,2

0,02 0,1

S p_il_i = 3,12

Середня довжина даного коду: 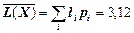(біт/сим).

Отже, ефективність коду,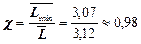

надлишковість коду.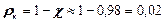

II Метод Хаффмена:

Побудуємо кодове дерево за алгоритмом Хаффмена, використовуючи ймовірності заданої д. в. в. (рис.1), і відповідно до кодового дерева побудуємо таблицю кодів (табл. 2):

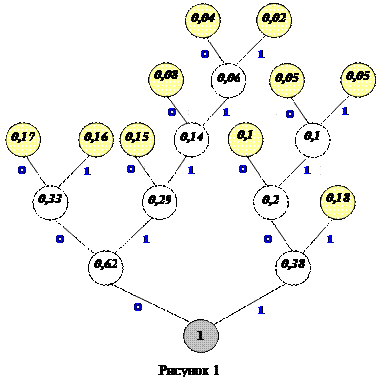
Таблиця 2

Імовірність p_i Код Code(x_i) Довжина коду l_i p_il_i

0,18 0,36

0,17 0,51

0,16 0,48

0,15 0,45

0,1 0,3

0,08 0,32

0,05 0,2

0,05 0,2

0,04 0,2

0,02 0,1

S p_il_i = 3,12

Середня довжина коду (біт/сим).

Отже, ефективність коду c=0,98, надлишковість r_к»0,02.

Для порівняння: при кодуванні даної д. в. в. рівномірним двійковим кодом середня довжина коду 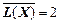(біт/сим), ефективність коду 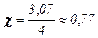, надлишковість r_к=1-c» 0,23 .

Задачі до розділу 3

1Побудувати код Шеннона-Фано для ансамблю повідомлень, заданого розподілом ймовірностей: 0,25; 0,25; 0,125; 0,125; 0,0625; 0,0625; 0,0625; 0,0625. Визначити середню довжину та ефективність коду.

2Сім рівноімовірних повідомлень кодуються кодом Шеннона-Фано. Визначити надлишковість коду.

3Побудувати коди Шеннона-Фано і Хаффмена для повідомлень джерела, заданого таким розподілом: P(x₁)=0,3; P(x₂)=0,2; P(x₃)=0,15; P(x₄)=0,12; P(x₅)=0,1; P(x₆)=0,08; P(x₇)=0,03; P(x₈)=0,02. Обчислити середню довжину і надлишковість отриманих кодів.

4Побудувати коди Шеннона-Фано і Хаффмена для дискретної випадкової величини (д. в. в.) Х, заданої розподілом ймовірностей:

X

P 7/18 1/6 1/6 1/6 1/9

Обчислити середню довжину отриманих кодів та ентропію д. в. в. X.

5Побудувати коди Хаффмена і обчислити середню довжину кодів для ансамблів повідомлень, заданих такими розподілами ймовірностей:

а) 0,16; 0,2; 0,14; 0,4; 0,02; 0,03; 0,05; б) 0,16; 0,11; 0,04; 0,12; 0,07; 0,07; 0,09; 0,03; 0,1; 0,02; 0,02; 0,01; 0,06; 0,04; 0,01; 0,05; в) 0,15; 0,35; 0,2; 0,03; 0,02; 0,05; 0,1; 0,04; 0,06; г) 0,07; 0,1; 0,03; 0,05; 0,05; 0,16; 0,08; 0,14; 0,1; 0,1; 0,04; 0,01; 0,03; 0,02; 0,02.

6Побудувати коди Шеннона-Фано і Хаффмена,обчислити їх середню довжину для ансамблів повідомлень, заданих такими розподілами ймовірностей: а) 0,06; 0,25; 0,1; 0,05; 0,2; 0,04; 0,3; б) 0,5; 0,3; 0,1; 0,025; 0,025; 0,02; 0,015; 0,015; в) 0,15; 0,1; 0,05; 0,25; 0,02; 0,03; 0,4.

Розділ 4 ЗАСТОСУВАННЯ СТАТИСТИЧНИХ АЛГОРИТМІВ СТИСНЕННЯ ДО БЛОКІВ ПОВІДОМЛЕННЯ

4.1 Теоретичні границі стиснення інформації

Стиснення даних не може бути більше деякої теоретичної границі. Сформульована раніше теорема Шеннона про кодування каналу без шуму встановлює верхню границю стиснення інформації як ентропію джерела H(X).

Позначимо через L(X) функцію, що повертає довжину коду повідомлень

L(X)=len(code(X)),

де code(X) кожному значенню X ставить у відповідність деякий бітовий код; len( ) - повертає довжину цього коду.

Оскільки L(X) - функція від д. в. в. X, тобто також є д. в. в., то її середнє значення обчислюється як математичне сподівання:

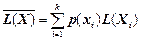. (2.3)

Наслідком теореми Шеннонапро кодування джерела у відсутності шуму є те, що середня кількість бітів коду, що припадає на одне значення д. в. в., не може бути менше її ентропії,тобто

(2.4)

для будь-якої д. в. в. X і будь-якого її коду.

Нехай 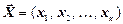- вектор даних завдовжки n; - вектор частот символів у .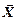

Тоді середня кількість бітів коду на одиницю повідомлення 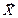обчислюється так:

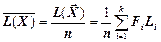, (2.5)

де - довжина коду повідомлення 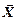: 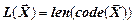; 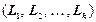- вектор Крафта для .

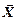Ентропія повідомлення 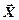обчислюється так:

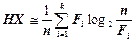. (2.6)

Розглянемо функцію y=ln(x), яка є опуклою вниз, тобто її графік лежить не вище своєї дотичної y=x-1. Тоді можна записати таку нерівність:

ln(x) £ x-1, x>0. (2.7)

Підставимо в (2.7) 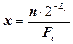і помножимо обидві частини цієї нерівності на :

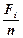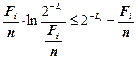. (2.8)

Запишемо суми за i обох частин нерівності (2.8), і з урахуванням того, що для оптимального кодування Хаффмена нерівність Крафта (2.1) переходить в строгу рівність, дістанемо в правій частині (2.8) нуль, отже,

.

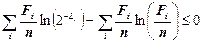Перейдемо від натурального логарифма до двійкового і з урахуванням виразу (2.6) дістанемо

,

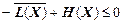тобто приходимо до виразу (2.4), що визначає верхню границю стиснення даних.

Припустимо, що у векторі Крафта 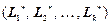довжини кодових слів пов'язані з частотами символів у повідомленні так:

.

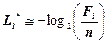При виконанні цієї умови нерівність Крафта (2.1) обертається у строгу рівність, і код буде компактним, тобто матиме найменшу середню довжину. Тоді, оскільки для оптимальних кодів Шеннона-Фано і Хаффмена довжина кожної кодової комбінації округлюється до більшої цілої кількості бітів, маємо

,

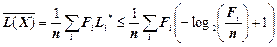звідси

.

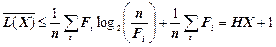Таким чином, границі стиснення інформаціїпри оптимальному статистичному кодуванні визначаються так:

. (2.9)

4.2 Метод блокування повідомлення

На відміну від раніше розглянутих методів кодування блокові кодиналежать до так званих кодів з пам'яттю, якщо всі його блоки мають довжину k символів.

Метод блокування повідомленьполягає в такому.

За заданим e>0 можемо знайти таке k, що якщо розбити повідомлення на блоки завдовжки k (всього буде n/k блоків), то, використовуючи оптимальне статистичне кодування таких блоків, що розглядаються як одиниці повідомлень, можна досягти середньої довжини коду більше ентропії менш ніж на e.

Припустимо, що X₁, X₂, …, X_n – незалежні д. в. в., що мають однаковий розподіл ймовірностей. Тоді ентропія n-вимірної д. в. в.

.

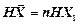Нехай 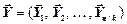- повідомлення джерела, де 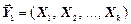, , 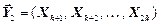… , 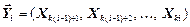- блоки повідомлення. Тоді

. (2.10)

При оптимальному кодуванні k-послідовностей векторної д. в. в. 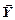, що розглядаються як одиниці повідомлення, справедлива нерівність

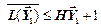. (2.11)

Середня кількість бітів на одиницю повідомлення X

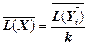. (2.12)

Тоді з урахуванням (2.10) і (2.12) нерівність (2.11) можна записати так:

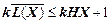. (2.13)

Розділивши обидві частини (2.13) на k, отримуємо

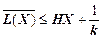, (2.14)

тобто достатньо вибрати .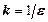

Приклад 1 Стиснемо вектор даних X=(0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1), використовуючи блоковий код 2-го порядку.

Розіб'ємо вектор на блоки довжини 2: (01, 10, 10, 01, 11, 10, 01, 01). Розглядатимемо ці блоки як елементи нового алфавіту {01, 10, 11}. Визначимо вектор частот появи блокових елементів в заданій послідовності. Одержуємо (4, 3, 1), тобто найбільш часто трапляється блок 01, потім 10 і найменше - 11; всього 8 блоків. Код Хаффмена для блоків символів представимо у вигляді кодового дерева (рис. 2) і відповідної таблиці кодів (табл. 2.5).

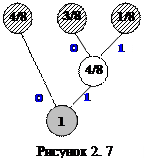Таблиця 2.5

Блок повідомлення Кодове слово

Замінюючи кожний блок повідомлення відповідним кодовим словом з таблиці кодів, дістанемо вихідну кодову послідовність Code(01, 10, 10, 01, 11, 10, 01, 01)= 010100111000.

Обчислимо ентропію, використовуючи статистичний розподіл ймовірностей символів повідомлення:

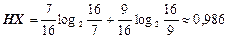(біт/сим).

Швидкість стиснення даних (середня довжина коду)

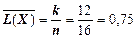(біт/сим).

Отриманий результат виявляється меншим за ентропію, що, здавалося, суперечить теоремі Шеннона. Проте це не так. Легко бачити з вектора початкових даних, що символ 0 частіше слідує 1, тобто умовна імовірність p(1/0) більше безумовної p(1). Отже, ентропію цього джерела необхідно обчислювати як ентропію статистично взаємозалежних елементів повідомлення, а вона менша за безумовну.

Приклад 2 Нехай д. в. в. X₁, X₂, …, X_n незалежні, однаково розподілені і можуть набувати тільки два значення 0 та1 з такою ймовірністю: P(X_i=0)=3/4 та P(X_i=1)=1/4, i=1…n.

Тоді ентропія одиниці повідомлення

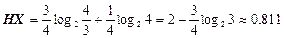(біт/сим).

Мінімальне префіксне кодування - це коди 0 або 1 завдовжки 1 біт. Отже, середня кількість бітів на одиницю повідомлення (біт/сим).

Розіб'ємо повідомлення на блоки довжиною n=2. Закон розподілу ймовірностей і відповідне кодування двовимірної д. в. в. наведені у табл. 2.6.

Таблиця 2.6

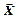
P 9/16 3/16 3/16 1/16

Префікс ний код

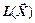
У цьому випадку середня кількість бітів на одиницю повідомлення 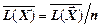=(1×9/16+2×3/16+3×3/16)/2=27/32»

»0,84375 (біт/сим), тобто менше, ніж для неблокового коду.

Для блоків довжини три середня кількість бітів на одиницю повідомлення≈0,823, для блоків довжини чотири – 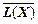≈0,818 і т. д.

Додамо, що формули теоретичних границь стиснення задають границі для середньої довжини коду на одиницю повідомлення – на окремих же повідомленнях степінь стиснення даних може бути меншим за ентропію.

Зразки розв'язування задач до розділу 4

Приклад 1 Дискретна випадкова величина (д. в. в.) X задана таким розподілом ймовірностей: P(X=A)=1/3; P(X=B)=7/15; P(X=C)=1/5. Побудувати таблицю кодів для блокового коду Хаффмена 2-го порядку. Визначити середню довжину коду.

Переглядів: 3802

<== попередня сторінка | наступна сторінка ==>

Розв'язання | Розв'язання

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.035 сек.