Метод фазової площини

Опис руху системи у вигляді залежності узагальненої координати від часу 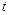не є єдиним. Стан системи в будь-який момент часу визначається двома значеннями: координати 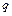і швидкості 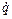; воно може бути представлено у плоскій декартовій системі координат точкою. Таку точку називають зображуючою точкою, а площину – фазовою площиною.

При русі системи величини і 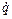змінюються, а отже, що зображаюча точка буде змінювати своє положення на фазовій площині. Геометричне місце зображують точок для заданого руху називається фазовою траєкторією. Сукупність усіх можливих фазових траєкторій системи називають її фазовим портретом.

Звернемося до рівняння (1.3). Враховуючи, що , і або його можна переписати в фазових змінних

Хоча порядок рівняння знижений на одиницю, але воно стало нелінійним. В даному випадку рівняння легко інтегрується поділом змінних і рівняння фазових траєкторій має вигляд

(1.5)

які є рівняннями еліпсів. Постійна визначається початковими умовами: . Початкові значення цих величин характеризують вихідні положення зображаючою точки.

Таким чином, вся фазова площина заповнена вкладеними один в одного еліпсів з центром в початку координат (рис. 1.4).

Напрями руху зображують точок показані на рисунку стрілками: позитивна швидкість відповідає збільшенню координати, негативна - зменшенню. Взагалі, структура фазових траєкторій дає

Рисунок 1.4 – Фазовий портрет лінійного осцилятора

тільки якісні особливості можливих рухів системи, але показує ряд найбільш характерних її властивостей.

У якісної теорії диференціальних рівнянь встановлюється, що через кожну точку фазової площини проходить одна і лише одна фазова траєкторія, за винятком тих точок, в яких похідна не визначена. Так в даному випадку в стані рівноваги (узагальнена швидкість дорівнює нулю) маятника похідна (1.6)

не визначена. Такі точки називаються особливими точками; через таку точку проходить або більше ніж одна фазова траєкторія, або не проходить жодної. На фазовому портреті (рис. 1.4) видно, що через початок координат не проходить жодна з фазових траєкторій; точки називають особливими точками типу «центр». З (1.6) також витікає, що дотична до фазової траєкторії в точках перетину траєкторії з віссю 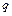перпендикулярна цієї осі.

Якщо в рівнянні (1.3) замінити на 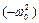, що відповідає випадку «негативної жорсткості», то рівняння фазових траєкторій прийме вигляд:

Фазові траєкторії складаються з сімейства гіпербол (рис. 1.5) і чотирьох півпрямі , є асимптотами цих гіпербол. Зображуючі точки на будь-якій траєкторії монотонно віддаляються від свого початкового положення, яке характеризує обурення стану рівноваги. Винятки становлять зображують точки на прямій. Система буде прагнути до стану рівноваги, але воно виявиться нестійким: Будь-яке як завгодно мале порушення умови призведе до необмеженого видаленню від стану рівноваги. Особлива точка називається точкою сідлової або сідлом.

Рисунок 1.5 – Фазовий портрет лінійного осцилятора:

Реальною механічною системою з «негативною жорсткістю» може служити перевернутий маятник (рис. 1.6), де наведений коефіцієнт жорсткості

Рисунок 1.6 – Перевернутий маятник

<== попередня сторінка	\|	наступна сторінка ==>
Лінійні коливальні системи без тертя	\|	Вільні коливання систем з нелінійною відновлювальною силою. Метод послідовних наближень

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.002 сек.