Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Вільні коливання систем з двома ступенями свободи

Розглянемо вільні коливання механічної системи, що має два ступені свободи. Прикладами таких систем є: механічна система пов'язаних маятників (рис. 4.1), пов'язані електричні контури (рис. 4.2), трьохатомна молекула (рис. 4.3).

Рисунок 4.1– Пов'язані маятники

Рисунок 4.2 – Коливальні контури з індуктивним зв'язком

Рисунок 4.3 - Трьохатомна молекуда води

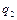Використовуючи вирази кінетичної і потенційної енергій системи в узагальнених координатах і , рівняння Лагранжа призводять до диференціальних рівнянь вільних коливань виду

(4.1)

Уявімо систему (4.1) у формі

(4.2)

звідки видно, що ліві частини є рівняннями лінійних консервативних систем, а праві частини характеризують сили зв'язку між ними. Коефіцієнти 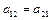, характеризують зв'язок між так званими парціальними системами.

Будь-яку складну систему з двома ступенями свободи можна розглядати як систему, що складається з двох окремих систем з одним ступенем свободи, пов'язаних один з одним. Ці окремі системи називають парціальними. Зв'язність систем означає, що коливання в одній системі впливають на коливання в інший і навпаки.

Приймемо для подальшого вивчення коливання системи, що парціальна система, відповідна даної незалежної координаті, отримана з повної, коли всі координати системи, крім данної, рівні тотожно нулю.

З (4.2) видно, що парціальні частоти рівні

, .

З властивостей позитивної визначеності квадратичних форм Т та П випливає, що

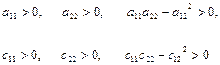(4.3)

(критерій Сильвестра).

Приватні рішення системи (4.1) шукаємо у вигляді простого гармонійного закону:

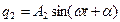, . (4.4)

Підставляючи (4.4) в рівняння (4.1) одержимо рівняння для амплітуд

(4.5)

Позначимо відношення узагальнених координат, рівне відношенню амплітуд коливань, через

. (4.6)

Нетривіальне рішення системи (4.5) буде тільки в тому випадку, коли її визначник дорівнює нулю, що дає рівняння власних частот коливань

. (4.7)

або

(4.8)

Досліджуємо функцію . Коефіцієнт при (див. 4.8) і вільний член більше нуля згідно критерію Сильвестра (4.3): це означає, що графік функції є парабола з гілками, спрямованими вгору. З (4.8) видно, що при рівної однієї з парціальних частот та . Корені рівняння (4.8) визначають власні частоти системи.

Зобразимо графік функції (рис. 4.4).

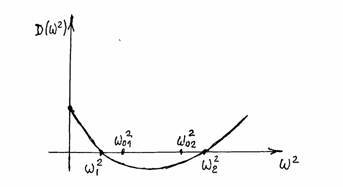
Рисунок 4.4 – Закон розподілу власних частот системи

Графік ілюструє відому теорему Релея: нижча частота власних коливань системи завжди менше найменшої парціальної частоти , а вища частота завжди більше найбільшої парціальної частоти .

Відповідні частотам і коливання називають головними коливаннями системи. Меншу з частот називають основною частотою, а перше головне коливання називають основним коливанням (воно є основним у результуючому русі системи). Визначивши і , з рівняння (4.8) знайдемо два значення , відповідні кожному з головних коливань:

(4.9)

Величини , характеризують форми головних коливань і їх називають коефіцієнтами розподілу амплітуд, тобто вони показують у скільки разів амплітуда відповідного коливання в одній з координат більше (або менше) амплітуди іншої координати.

Позначивши значення узагальнених координат і амплітуд коливань, відповідних першому головному коливанню, індексом (1), маємо

(4.10)

для другого головного коливання - індексом (2), то

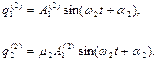(4.11)

Загальне рішення системи диференціальних рівнянь (4.1) виходить шляхом підсумовування приватних рішень

(4.12)

де , , і знаходяться з початкових умов.

Висновки:

1. Рішення (4.12) показує, що кожне з головних коливань окремо є простим гармонійним коливанням, але результуючий рух являє собою складний рух.

2. Якщо система здійснює одне з головних коливань (див. 4.12), то обидві узагальнені координати змінюються синхронно, тобто мають однакові частоти і фази коливань.

3. У кожному з головних коливань амплітуди знаходяться в постійному співвідношенні ( або ), що не залежить від початкових умов і залежить тільки від структури системи.

Биття

Розглянемо систему з двома ступенями свободи за умови близькості власних частот: . Тоді рішення (4.12) для узагальненої координати, наприклад,

(4.13)

можна записати у вигляді

(4.14)

Введемо позначення:

и ,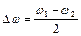

які називають «середньою» частотою і частотою «модуляції» відповідно. Замість (4.14) зручно записати

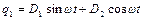, (4.15)

де , – повільно мінливі періодичні функції часу.

Остаточно отримуємо замість (4.13) функцію

, (4.16)

де , ,

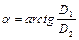тобто рух носить синусоїдальний характер з амплітудою, що періодично повільно змінюється. Графік зміни зображений на рис. 4.5 .

Рисунок 4.5 – Графік биття однієї узагальненої координати

Такі коливання називаються биттям. Рух, відповідний координаті 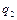, також відбувається за законом биття, але зрушеним по фазі щодо . Цей факт свідчить про обмін енергією між ступенями свободи.

Відзначимо, що в будь-якій системі з двома ступенями свободи можна створити биття.

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Нормальні координати

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.