- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Вимірів однієї величини
Завдання|задача| знаходження найбільш надійних значень вимірюваних|вимірів| величин призводить|призводить| до розв’язання інших завдань|задач|, зокрема визначення точності результатів оцінювання вимірів|вимірів|. Очевидно, що на основі одного виміру|виміру| оцінити|оцінювати| точність отриманого результату є неможливим. Однак, якщо буде відома велика кількість результатів вимірів|вимірів| певної величини і дійсні похибки, то, проаналізувавши їх, можна уникнути грубих похибок, а в деяких випадках і систематичних похибок. Після|потім| цього можна отримати|одержувати| ряд|лаву| випадкових дійсних похибок.
Розглядаючи|розглядувати| декілька рядів|лави| випадкових дійсних похибок, можна оцінити точність результатів вимірів|вимірів| за ступенем їх розкиду, тобто чим менше вони відрізняються один від одного, тим вони точніше, і навпаки – тим менш точними слід їх вважати.
Для оцінки точності результатів вимірів|вимірів| прийняті наступні критерії: середня похибка, імовірнісна похибка і середня квадратична похибка.
Середньою похибкою θ називають середнє арифметичне|із| абсолютних значень похибок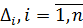 
результатів вимірів
Розглянемо|розглядуватимемо| довільний ряд|лаву| випадкових похибок результатів вимірів|вимірів| деякої величини.
Абсолютним варіаційним рядом|лавою| випадкових похибок називають послідовність цих похибок, розміщених в порядку зростання або убування за їх абсолютною величиною.
Ймовірнісною похибкою ρ називають таке значення абсолютного варіаційного ряду|лави| випадкових похибок, яке ділить даний ряд|лаву| на дві рівні частини.
Розглянемо|розглядуватимемо| такий ряд|лаву| випадкових похибок:
-0,01; 0,12; 0,56; -0,35; 0,06; -0,11; -0,05; -0,20; -0,08; 0,09; -0,19; -0,18; 0,32; -0,45; 0,30; -0,44; -0,57.
Побудуємо|спорудимо| абсолютний варіаційний ряд|лаву| або, іншими словами, ранжируємо ці величини без урахування їх знаків
0,01; 0,05; 0,06; 0,08; 0,09; 0,11; 0,12; 0,18; 0,19; 0,20; 0,30; 0,32; 0,35; 0,44; 0,45; 0,56; 0,57.
У середині цього ряду|лави| знаходиться|перебуває| значення 0,19. Отже ймовірнісна похибка вимірів ρ = 0,19 |вимірів|.
У наведеному прикладі|зразку| кількість значень N ряду|лави| похибок дорівнює непарному числу 17. Якщо кількість значень N ряду|лави| похибок дорівнює парному числу, то ймовірнісною похибкою буде середнє арифметичне двох значень абсолютного варіаційного ряду|лави|, які знаходяться|перебувають| у середині ряду|лави|.
Середньоквадратичною похибкою m називають величину, яка дорівнює квадратному кореню із|із| середнього арифметичного квадратів дійсних похибок
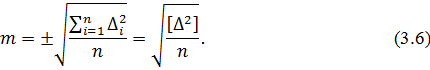
Середньоквадратична похибка є|з'являється| найбільш прийнятним|допустимим| критерієм для оцінювання точності вимірів|вимірів|. Вона має наступні|слідуючі| переваги порівняно із середньою і ймовірнісною похибками:
1. Середньоквадратична похибка є|з'являється| чутливою мірою точності тому, що на її величину сильно впливають великі за абсолютною величиною випадкові похибки, що визначають надійність результатів вимірів|вимірів|.
2. Середньоквадратична похибка вже за деякої відносно невеликої кількості вимірів|вимірів| набуває сталого значення і при збільшенні кількості вимірів|вимірів| змінюється незначно.
3. На основі середньоквадратичної похибки можна знайти граничну похибку (див. властивість обмеженості), тобто таке найбільше за абсолютною величиною значення випадкової похибки, яке може з'явиться|появлятиметься| за певних умов вимірів|вимірів|. Потрійна|потроєна|| середньоквадратична похибка приймається за граничну, тобто
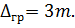(3.9)
4. Знаючи| середньоквадратичні похибки певних величин, можна легко визначити| середньоквадратичні похибки інших величин, функціонально пов'язаних з ними.
Гранична похибка Δгр, як і стандарт σ, залежать тільки|лише| від умов вимірів|вимірів|. Отже, між цими величинами повинна існувати певна залежність.
У теорії ймовірності|ймовірності| встановлено|установлений|, що, якщо випадкові погрішності розподілені за нормальним законом, вираженим|виказувати| формулою (3.1), то ймовірності|ймовірність| того, що |Δ| < 2σ = 0,9544; |Δ| < 3σ = 0,9974.
Це означає, що абсолютна величина випадкової похибки може бути більше 2σ лише в 5 випадках із|із| 100 можливих, а більше 3σ тільки|лише| в 3 випадках з|із| 1000 можливих.
Виходячи з цього і беручи до уваги те, що замість невідомого стандарту використовується| середньоквадратична похибка, в геодезії прийнято як граничну похибку приймати величини
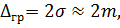(3.10)
а при відносно невеликій кількості вимірюваних величин або при особливо відповідальних вимірюваннях|вимірах|
(3.11)
Отже, якщо будь-який результат вимірів|вимірів| має похибку більшу за граничну, то такий результат містить|утримує| грубу похибку і тому має бути виключений з|із| подальшої|дальшої| обробки і замінений новим, отриманим|одержувати| під час|із| повторних вимірів|вимірів|.
В окремих випадках замість| середньоквадратичної похибки використовують середню похибку, яка обчислюється за формулою
У теорії ймовірності |ймовірність| доведено, що між величинами m і υ існують залежності
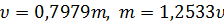(3.13)
Таким чином, усі точкові|крапкові| оцінки, так або інакше, пов'язані з | середньоквадратичною похибкою. Зі свого боку|своєю чергою|, величина m є|з'являється| наближеним значенням стандарту.
Виникає питання, на скільки і як швидко значення m, яке залежить від кількості вимірів|вимірів|, наближається до σ? Досліджуємо це на окремому прикладі|зразку| з|із| практики геодезичних вимірів|вимірів|.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | ОЦІНКА ТОЧНОСТІ ФУНКЦІЙ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |