Два підходи до розв’язання задачі зрівнювання

геодезичних побудов|шикувань|

Із попереднього підрозділу можна відмітити|помітити|, що при розгляді сутності і способів зрівнювання геодезичних побудов|шикувань| в їх основі лежить математичне поняття «рівняння» (умовні рівняння, рівняння похибок, нормальні рівняння та інші), яке на мові|язиці| алгебри представляє|уявляє| деяку модель процесу вимірів з урахуванням|з врахуванням| факторів, що впливають на цей процес. Багаторазові, у тому числі і надлишкові виміри в задачах зрівнювання, формально представляються у вигляді системи рівнянь, яку можна інтерпретувати як модель серії (ряду|лави|) вимірів.

Різноманіття і особливості вирішення геодезичних завдань приводить до того, що, як правило, процеси вимірів описуються невизначеними системами рівнянь, тобто недовизначеноюсистемою – система рівнянь (зазвичай диференціальних), число рівнянь в якій менше числа невідомих і перевизначеноюсистемою – система, число рівнянь якої більше числа невідомих. Наведемо на прикладах недовизначену і перевизначену системи рівнянь.

Приклад|зразок| 9.1.

Візьмемо трикутник, де виміряні|виміряти| три кути|роги|. Отже, має місце рівняння

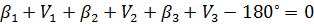де β – виміряні кути, V – поправки до вимірів. На рис. 9.1 вершині трикутника Авідповідає кут 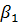, вершині Ввідповідає кут 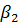, а вершині Скут 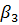. Позначимо 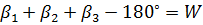, де W – нев'язка в трикутнику. Тоді справедливо записати

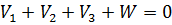. (9.1)

Отримано рівняння, яке містить три невідомих 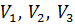і один вільний член W. Таке рівняння має безліч рішень, тобто система рівнянь, що складається з одного рівняння є недовизначеною.

Приклад|зразок| 9.2.

Розглянемо систему трьох нівелірних ходів з однією вузловою точкою С.При цьому вважатимемо висоту вузлової точки Н за невідому. Необхідно знайти цю висоту. Пояснимо дане завдання графічно (див. рис. 9.2).

Математична модель даної ситуації має вид:

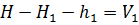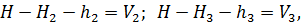; (9.2)

де Н₁, Н₂, Н₃ – висоти початкових реперів, h₁, h₂, h₃ – виміряні перевищення, Н – висота вузлової точки С. Таким чином, маємо три рівняння з одним невідомим, тобто система рівнянь (9.2) є перевизначеною і має, також як і у прикладі 9.1, безліч рішень.

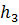
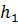
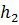
Рис. 9.2 – Система нівелірних ходів з вузловою точкою

Практика показує, що процес зрівнювання геодезичних побудов|шикувань| завжди описується невизначеними|неозначеними| системами рівнянь, які не мають єдиного розв'язання, тобто не можуть бути розв’язані|рішати| способами елементарної алгебри – способами підстановки, порівняння, складання, графічним способом або способом визначення. Метод вирішення невизначених|неозначених| систем рівнянь був запропонований на початку XIX ст.|ст| німецьким математиком і геодезистом К.Ф. Гаусом (1777 – 1855) і французьким математиком А.М. Лежандром, який отримав|одержував| назву методу найменших квадратів.

<== попередня сторінка	\|	наступна сторінка ==>
Сутність задачі зрівнювання результатів вимірів в геодезії	\|	Сутність методу найменших квадратів і обґрунтування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.