Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Додавання та віднімання в межах першого десятка. Випадки додавання і віднімання, пов’язані з нумерацією чисел.

ЗМІСТОВИЙ Модуль IIІ

МЕТОДИКА НАВЧАННЯ АРИФМЕТИЧНИХ ДІЙ ТА ФОРМУВАННЯ ОБЧИСЛЮВАЛЬНИХ НАВИЧОК

Лекція 7-10

ТЕМА. Методика навчання арифметичних дій (додавання та віднімання) та формування обчислювальних умінь і навичок. (8 год).

Мета:вивчення теми «методика навчання арифметичних дій (додавання та віднімання) та формування обчислювальних умінь і навичок», ознайомлення з методикою введення арифметичних дій додавання і віднімання в початковій школі; розвиток професійного мислення студентів; виховання поваги до професії вчителя.

План:

1. Додавання та віднімання в межах першого десятка. Випадки додавання і віднімання, пов’язані з нумерацією чисел.

2. Складання і засвоєння таблиць додавання і віднімання з переходом через десяток.

3. Усне і письмове додавання та віднімання без переходу та з переходом через десяток в межах сотні.

4. Методика навчання додавання та віднімання в межах 1000.

5. Методика навчання додавання і віднімання багатоцифрових чисел.

Самостійно: “Додавання та віднімання іменованих чисел” (Коваль Л.В., Скворцова С.О. Методика навчання математики: теорія і практика. - Х.: ЧП «Принт-Лідер», 2011. - 414 с. – с.239-240.)

Література

Основна:

1. Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах: Навч. пос.. – 3-є вид., перероб. і доп. – Тернопіль: Навчальна книга – Богдан, 2006. – С. 106-206с.

2. Коваль Л. В., Скворцова С. О. Методика навчання математики: теорія і практика: Підручник для студентів за спеціальністю 6.010100 „Початкове навчання”, освітньо-кваліфікаційного рівня „бакалавр” [2-ге видання допов. І переробл.] – Харків: ЧП „Принт-Лідер”, 2011. – С. 106-160.

3. Стрілець С.І. Методика викладання математики в початкових класах у таблицях і схемах: навч.-метод. посіб. / С. І. Стрілець.– Чернігів: Чернігівський національний педагогічний університет імені Т.Г.Шевченка, 2012. – С. 57-60.

Додаткова:

1. Богданович М. В. Методика вивчення нумерації арифметичних дій у початковій школі. – К., 1991. – 206с.

2. Корчевська О. П. Навчаємо математики. Методика обчислень. 1-4 класи. – Тернопіть: Мандрівець, 2009. – 156с.

3. Скворцова С.О. Методика навчання математики в 1-му класі: методичний посібник для вчителів перших класів та студентів за спеціальністю 6.010100 «Початкове навчання», освітньо-кваліфікаційного рівня «бакалавр» / С. О. Скворцова. – Одеса: Фенікс, 2011. – 240 с.

Додавання та віднімання в межах першого десятка. Випадки додавання і віднімання, пов’язані з нумерацією чисел.

Ознайомлення учнів з конкретним змістом арифметичних дій додавання і віднімання відбувається під час оперування множинами предметів. Об'єднуючи елементи двох множин, що не перетинаються, знаходимо численність поєднаної множини. Операція об'єднання двох множин, що не перетинаються, розкриває конкретний зміст дії додавання.

Операція утворення доповнення до підмножини формує зміст дії віднімання. Численність множини, що залишилася після вилучення частини її елементів, відповідає остачі. Операція вилучення частини елементів множини розкриває конкретний зміст дії віднімання.

Під час пояснення змісту арифметичних дій в початковій школі доцільно використовувати принцип співвіднесення предметної, вербальної, схематичної і символічної моделей і перехід від однієї моделі до іншої. Такий підхід особливо важливий з точки зору подальшого навчання учнів розв'язування задач.

За методичною системою М.В. Богдановича, підготовка до опрацювання дій додавання та віднімання розпочинається з перших уроків математики та зводиться до знаходження суми або різниці двох предметних множин перелічуванням, що неможливо зробити без предметів чи малюнків.

У вивченні дій додавання та віднімання в межах 10 за методичною системою М.В Богдановича можна виділити такі етапи.

1. Знаходження суми або різниці двох предметних множин перелічуванням предметів (ці операції виконуються на підготовчому етапі при вивченні нумерації чисел).

2. Ознайомлення спочатку з дією додавання, а потім віднімання; зв'язок між ними та символікою цих дій (така робота також здійснюється під час вивчення нумерації).

3. Ознайомлення з назвами компонентів і результатом дії додавання (безпосереднє ознайомлення з назвами компонентів і результатом дії віднімання відбувається значно пізніше).

4. Складання і заучування таблиць додавання та віднімання в межах 10; застосування табличних результатів для обчислення виразів на дві дії (однакових чи різних).

5. Ознайомлення з прийомами додавання та віднімання числа частинами (групами), а також переставною властивістю дії віднімання.

Основні характеристики методичної системи М.В. Богдановича:

Процес первинного ознайомлення з діями додавання та віднімання. Оознайомлення з діями додавання та віднімання розмежовується в часі (після вивчення числа і цифри 5 діти ознайомлюються з дією додавання, а після вивчення числа і цифри 7 з дією віднімання), що пояснюється складністю засвоєння математичної термінології, для якої потрібен додатковий час;

Послідовність ознайомлення учнів з назвами компонентів і результатами дій додавання та віднімання. За методичною системою М.В. Богдановича ознайомлення учнів з назвами компонентів і результатом дії додавання відбувається на початку вивчення теми „Додавання та віднімання в межах 10", а з назвами компонентів і результатом дії віднімання наприкінці першого класу;

Особливості ознайомлення учнів з додаванням та відніманням у межах 10. М.В. Богданович пропонує вивчення теми „Додавання та віднімання в межах 10" розпочинати зі складання і заучування таблиць додавання та віднімання в межах 10, оскільки ознайомлення зі складом числа та з додаванням і відніманням в межах кожного числа доцільно опрацьовувати паралельно ще під час ознайомлення з нумерацією в межах 10.

За методичною системою М.В. Богдановича основний прийом обчислення під час вивчення кожної таблиці додавання і віднімання в межах 10 - це склад числа та взаємозв'язок дій додавання і віднімання.

Розкриємо докладніше ще один з методичних підходів, під час опрацювання дій додавання та віднімання в межах 10, який відповідає вимогам Державного стандарту початкової загальної освіти та нової навчальної програми для учнів початкової школи.

На етапі вивчення нумерації чисел в межах 10, ще до введення дій додавання і віднімання діти виконують завдання по оперуванню предметними множинами, тобто відбувається підготовча робота.

Підготовча робота до ознайомлення з діями додавання та віднімання здійснюється за допомогою практичних вправ, під час яких діти викладають на парті геометричні фігури та об'єднуючи їх, показують усі фігури. Таким чином, спочатку формується поняття про об'єднання елементів двох множин, що не перетинаються. Діти дістають висновку, щоб показати всі предмети, треба їх об'єднати - це означає присунути, змішати тощо. Аналогічно діти вправляються у виключенні частини множини та показу остачі. Щоб показати остачу, решту, треба виключати - це означає відсунути, забрати, відрізати тощо.

Перелічуючи кількість елементів об'єднаної множини діти впевнюються в тому, що коли об'єднуємо стає більше; щоб стало більше, треба об'єднати. Коли виключаємо стає менше, щоб стало менше, треба виключати.

Наступним кроком є схематичне зображення операцій об'єднання чи виключення. Спочатку діти виконують аналогічні завдання практично, а потім виконують рисунок. Об'єднуючи - обводять замкненою кривою лінією усі фігури, виключаючи - закреслюють кілька фігур та обводять замкненою кривою остачу. Після того, як діти навчилися зображати об'єднання або виключення схематично за допомогою геометричних фігур, переходимо до навчання схематичного зображення за допомогою відрізків.

На наступному етапі здійснюється ознайомлення з конкретним змістом арифметичних дій додавання та віднімання: вчимо дітей пов'язувати практичну дію об'єднання елементів двох множин з арифметичною дією додавання, а практичну дію щодо виключення частини елементів хмножини з арифметичною дією віднімання. Таким чином формується поняття про те, що коли додаємо стає більше, а коли віднімаємо залишається менше. На цьому етапі також відбувається ознайомлення учнів із знаками додавання та віднімання: навчання їх запису; вводяться поняття „вираз", „значення виразу". З цією метою доцільно пропонувати вправи типу:

1. Покладіть на парту зліва 5 червоних квадратів. Покладіть справа 2 жовті квадрати. Присуньте жовті квадрати до червоних. Покажіть всі квадрати. Що ми зробили з квадратами? Ми присунули - об'єднали! Всього квадратів 5 і ще 2.

Коли квадрати об'єднали, їх стало більше. Об'єднати - це означає додати. Додавання - це арифметична дія, яка виконується між числами. Таким чином, 5 і ще 2 - це значить до 5 додати 2, одержимо 7. Це можна записати так: 5+2 = 7

Коли об'єднуємо стає більше. Об'єднати - це означає додати. Тому, коли додаємо стає більше. Щоб стало більше треба об'єднати - додати!

2. Поклади на парту 8 кружків. З круги відсунь. Покажи круги, що залишилися. Що ми зробили? Ми відсунули -виключили! Залишилося кругів 8 без 3.

Коли круги виключили, їх стало менше, ніж було! Виключити - це означає відняти. Віднімання - це арифметична дія, яка виконується між числами. Таким чином, 8 без 3 - це значить із 8 відняти 3, одержимо 5. Це можна записати так: 8-3=5.

Коли виключаємо стає менше. Виключити - це означає відняти. Тому, коли віднімаємо стає менше. Щоб спало менше треба відняти!

Учні розглядають зроблені записи: 5 + 2 = 7 та 8 - 3 - 5, і з'ясовують, що в них спільною є наявність знаку рівності, то їх можна назвати одним словом „рівність". Ліворуч від знака рівності записані числа, що поєднані знаком плюс або мінус : 5 + 2 та 8 - З - це вирази. Праворуч від знака рівності записані числа 7 або 5 -це значення виразів.

З метою первинного закріпленні конкретного змісту арифметичних дій додавання і віднімання учні до малюнків, на яких проілюстровано об'єднання або вилучення складають вирази чи рівності; перевіряють чи правильно складено до малюнку вираз або рівність, виправляють помилки, якщо вони є. Наприклад:

Практичні вправи на об'єднання або виключення доповнюються завданням на складання виразу з карток з числами й знаками арифметичних дій та знаходження значення виразу тощо.

Далі діти вибирають вираз до схематичного рисунку або, навпаки, схематичний рисунок до виразу:

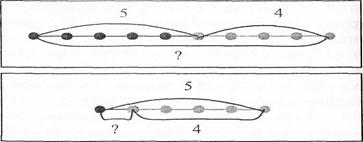
Також учні складають по дві рівності на додавання і дві на віднімання за рисунками, на яких множину геометричних фігур розбито на дві підмножини за спільною ознакою (кольором; розміром; формою), або за картками „доміно", або за схемами, що складаються з двох відрізків.

Аналогічним чином, на підставі конкретного змісту арифметичних дій додавання і віднімання, складаємо по дві рівності на додавання та дві - на віднімання на підставі складу числа.

На цьому старі навчання виконуємо додавання та віднімання за числовим променем:

5 + 2 = 7 - 4 =

Додаючи числа крокуємо „вперед" - праворуч, а віднімаючи -„назад" - ліворуч, на стільки кроків, скільки вказує число, що записано у виразі на другому місці.

Назва компонентів і результату арифметичної дії додавання.

Ознайомлюючи учнів з назвами компонентів і результатом арифметичної дії додавання, їм пропонується практичне завдання: покласти на парту 4 зелені та 3 червоні кружечки, об'єднати ці кружечки, скласти та прочитати вираз.

- Ми до 4-х додаємо 3. Числа, які додають, називають доданками. Таким чином, 4 та 3 - це доданки: 4 - це перший доданок, 3 - це другий доданок.

- Перерахуйте кружечки або додайте 3 червоні кружечки по одному. Запишіть рівність: 4 + 3 = 7. Ми отримали в результаті додавання число 7? Число, яке отримують в результаті дії додавання називають значенням суми. Число 7 - це значення суми.

Далі переходимо до схематичного зображення доданків та суми. Наприклад:

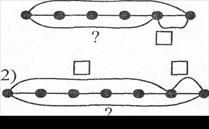
- Виберіть схему до малюнка: 1)

Покажіть усі кружечки. Щоб дізнатися, скільки всього кружечків, треба об'єднувати. Тож назвіть схему, на якій відрізок, позначений знаком запитання, є об'єднанням двох відрізків (такою схемою є друга).

Більше число знаходимо дією додавання. Складаємо вираз: 5 + 1. Число 5 — перший доданок. Число 1 другий доданок. Знаходимо значення виразу. Число 6 - значення суми. Показуємо на схемі перший доданок, другий доданок, значення суми. Відтепер діти читають рівності із назвами компонентів та результатом дії додавання. У записах рівностей учням пропонується підкреслити перший доданок однією рискою, другий доданок - двома рисками, а значення суми - хвилястою лінією.

Математичний вираз " сума". Опрацювання зазначеної теми розпочинається з читання рівностей з назвами компонентів.

5 + 1 = 6

1-й доданок 2-й доданок значення суми

Після чого вчитель повідомляє, що вираз, який записано ліворуч від знака „=", називається так само, як і результат -„сума". Якщо між числами стоїть знак „+", то записана сума. Щоб записати суму, треба між числами поставити знак „+", а, щоб знайти значення суми, треба ці числа додати! Отже, треба розрізняти поняття „сума" як назву виразу та „значення суми" - як числове значення виразу.

На етапі первинного закріплення діти підкреслюють або записують математичні вирази „суми" двох даних чисел.

Переставний закон додавання. Ознайомлення з переставним законом додавання здійснюємо через співставлення рівностей, що складені за карткою „доміно", і підводимо дітей до формулювання закону на підставі індуктивних узагальнень.

За числовими фігурами складіть рівності на додавання. Прочитайте рівності. Що цікавого ви помітили?

- Прочитайте першу рівність: перший доданок 5, другий

доданок 4, значення суми 9.

- Прочитайте другу рівність: перший доданок 4, другий доданок 5, значення суми 9. Що помітили? (Перший доданок став другим, а другий доданок став першим, значення суми від цього не змінилося). Після виконання завдання учні роблять висновок: у цих рівностях переставили доданки: перший доданок став другим, а другий, навпаки, - першим; значення суми від цієї перестановки не змінилося.

Аналогічне завдання можна запропонувати учням з відрізками:

1. Порівняйте суми. Чим вони схожі? Чим відрізняються? Що можна сказати про результати сум? Чому?

5 + 2 3 + 4 7 + 1 5 + 6 8 + 7 4 + 9 7 + 3
2 + 5 4 + 3 1 + 7 6 + 3 7 + 8 4 + 6 3 + 7

Коментар: перший доданок 5, другий доданок 2; перший доданок 2, другий доданок 5; ці вирази схожі тим, що в них однакові доданки, а відрізняються порядком запису доданків; доданки переставили, від цього значення суми не змінюється, тому ці вирази мають однакові значення...

Не мають однакових значень вирази: у 4-му стовпчику та з 6-му, тому що в них доданки неоднакові.

Доцільно познайомити учнів із застосуванням переставного
закону у випадку трьох доданків і познайомити учнів з іншим його
формулюванням: додавати числа можна в будь-якому порядку. Це
правило дуже спрощує обчислення у випадках трьох доданків,
коли значення суми двоцифрове число.

Взаємозв'язок між діями додавання і віднімання. Познайомити учнів з взаємозв'язком додавання і віднімання можна за допомогою наочного посібника:

1-й доданок 2-й доданок

сума

Якого кольору відрізок, що ілюструє 1 перший доданок? Другий доданок? Суму? З чого складається сума?

Аркушем паперу прикриваємо на схемі по черзі перший, а потім другий „доданок". Визначаємо, що залишилось. Коли прикрили аркушем один з „доданків", ми виключили. Учні дістають висновку: якщо від суми двох доданків відняти один доданок, то одержимо інший доданок.

Треба зазначити, що частіше в методичній літературі питання про взаємозв'язок дій додавання та віднімання розглядається як складання з однієї рівності на додавання двох рівностей на віднімання.

Тепер можна ввести означення дії віднімання. З цією метою діти коментують, як з однієї рівності на додавання склали дві рівності на віднімання: із суми відняли перший доданок і одержали другий доданок; із суми відняли другий доданок і одержали перший доданок. Знаходили один із доданків - із суми віднімали інший доданок.

Віднімання - це арифметична дія, при якій по значенню суми та одному доданку знаходять інший доданок.

8-3 = 5

8.-5 = 3, тому, що 3+5 = 8

Знаходження невідомого доданка. Ознайомлення з правилом знаходження невідомого доданка можна здійснити, створивши ситуацію, коли відомо значення суми і один доданок, а інший доданок невідомий. Наприклад: у Вані в двох руках 7 паличок. У правій руці 3 палички, а скільки паличок в лівій руці, він нам не показав, і порахувати ми їх не можемо. Як дізнатися, скільки паличок у Вані в лівій руці?

Учні міркують так: 7 паличок в обох руках, а в правій – тільки 3, отже, до числа 7 входять 3 палички, які Ваня тримає в правій руці; щоб дізнатися, скільки паличок у лівій руці, треба з 7-ми виключити 3.

Учні пояснюють за схематичним малюнком, що означають відомі числа та невідоме число, встановлюють, що відоме значення суми і другий доданок, отже треба знайти перший доданок. Згадують, як однержати перший доданок, і дістають висновок: щоб знайти невідомий доданок, треба від значення суми відняти відомий доданок.

Математичний вираз „різниця". Ознайомлення з поняттям „різниця" можна здійснити, запропонувавши учням розбити вирази на дві групи.

5 + 1 7-2 4 + 2 9-2 6 + 2 10- 1 3 + 1

8 + 2 4 + 0 4-2 5 + 2 7-7 7 + 2 8-0

Учні розбивають вирази на групи згідно знаку, який стоїть між числами, тому до першої групи входять суми, а до другої - вирази, в яких між числами стоїть знак мінус. Назву виразів першої групи учні вже знають (якщо між числами записаний знак +, то це математичний вираз сума). У виразах другої групи між числами стоїть знак мінус, і вчитель повідомляє: „Якщо між числами стоїть знак мінус, то записано математичний вираз „різниця". Щоб записати різницю, треба між числами поставити знак мінус". Далі учні обчислюють значення сум і різниць.

На етапі первинного закріплення поняття „різниця" школярам пропонується обчислити спочатку значення різниць, а потім обчислити значення сум.

Назва компонентів дії віднімання. На початку вивчення теми вчитель повідомляє, що так само, як і при додаванні, при відніманні числа мають свої назви. Учні згадують, що при відніманні одержують менше число. Отже, при відніманні число, з якого ми віднімаємо зменшується, тому воно називається зменшуваним. Число, яке віднімають називається за характером дії від'ємник. І результат дії віднімання називається так само, як і вираз, що записано ліворуч від знака рівності, але зі словом „значення" — значення різниці.

5 - 1 = 4

зменшуване від'ємник значення різниці різниця від’ємник

Далі діти показують на схемі дужкою зменшуване, від'ємник і значення різниці; записують відповідні рівності. Також корисні завдання на складання рівностей під диктовку, наприклад:

1) зменшуване 6, від'ємник 1, зайти значення різниці (6 - 1 = 5);

2) перший доданок 5, другий доданок 2, знайти значення суми (5 + 2 = 8);

3) зменшуване 10, від'ємник 2, знайти значення різниці (10-2 = 8).

Також доцільно запропонувати школярам прочитати вирази з назвою компонентів та знайти їх значення. При обчисленні значень виразів пропонуємо в рівностях на віднімання підкреслити однією рискою зменшуване, двома - від’ємник, хвилястою лінією - значення різниці.

Правила знаходження невідомого зменшуваного, невідомого від'ємника. Познайомити учнів з цими правилами можна через аналіз схематичного зображення.

Зменшуване складається із значення різниці та від’ємника. Щоб знайти треба дозначення різниці додати від’ємник.

На кресленні із зменшуваного виключаємо значення різниці. Залишається від'ємник. Щоб знайти невідомий від'ємник,треба від значення зменшуваного відняти значення різниці.

Додавання і віднімання нуля. Віднімання однакових чисел. Після ознайомлення з числом нуль, учні вчаться виконувати додавання і віднімання з нулем. Ввести ці правила можна на підставі індуктивних узагальнень, пропонуючи учням проаналізувати кілька рівностей виду: 5 + 0 = 5, 0 + 5 = 5, 5-0 = 5, 5-5=0.

При додаванні (відніманні) нуля до (від) будь-якого числа в результаті отримаємо те ж саме число. При відніманні однакових чисел в результаті отримаємо нуль.

Методика складання таблиць додавання і віднімання. Перед вивченням таблиць додавання і віднімання окремого числа (1,2...9) слід сформувати в учнів відповідні обчислювальні навички! - цей найвищий ступінь оволодіння обчислювальними прийомами] Під прийомом обчислення розуміють систему операцій, яку потрібно виконати, щоб дія досягла своєї мети - це орієнтувальна основа дії (ООД). Таким чином, прийоми обчислення над числами складаються з ряду послідовних операцій (системи операцій)] виконання яких призводить до знаходження відповіді] арифметичної дії над цими числами, причому вибір операції в кожному прийомі встановлюється тими теоретичними положеннями, які використовуються як його теоретична основа.

Теоретичною основою додавання та віднімання 1 є знання порядку прямування чисел в натуральному ряді. Числа 2, 3, 4, 5 додають і віднімають частинами на підставі складу цих чисел (теоретична основа - правило додавання суми до числа).

Переставний закон додавання є теоретичною основою прийому додавання чисел 6,7,8,9. Числа 6,7,8,9 віднімають на підставі взаємозв'язку між діями додавання і віднімання.

Учні не повинні бездумно заучувати таблиці, вони мають знати спосіб обчислення і користуватися ним при знаходженні значень виразів. Тому спочатку формуємо відповідні обчислювальні навички і на останньому етапі складаємо таблиці. При ознайомленні і первинному закріпленні обчислювального прийому міркування подаються розгорнено і повністю промовляються вголос, потім вони поступово скорочуються і автоматизуються, в результаті чого учень набуває навички у виконанні даної дії.

Виходячи із груп прийомів обчислення в межах 10 слід дотримуватися такого порядку опрацювання таблиць додавання і віднімання: 1) додавання і віднімання числа 1; 2) додавання і віднімання числа 2; 3) додавання і віднімання числа 3; 4) додавання і віднімання числа 4; узагальнення прийому додавання і віднімання по частинах; 5) додавання на підставі переставного закону додавання: додавання чисел 5,6,7,8,9; 6) віднімання на підставі взаємозв'язку дій додавання і віднімання: віднімання чисел 5,6,7,8,9.

Методика формування обчислювальних навичок передбачає етапи: 1) ознайомлення з прийомом обчислення, надання учням орієнтувальної основи дії; 2) виконання учнями нової дії, спираючись на матеріалізовані опори картки з друкованою основою, пам'ятки; 3) розгорнене виконання дії з промовлянням уголос кожного кроку пам'ятки (спочатку читаючи кожне завдання пам'ятки, а потім — промовляючи своїми словами); 4) виконання дії з промовлянням „про себе" кроків пам'ятки; під час виконання дія скорочується — виконуються лише основні операції; 5) виконання дії в розумовому плані, дія максимально скорочується та автоматизується. На останньому етапі складаємо таблиці.

Збільшення або зменшення числа на кілька одиниць. Ознайомлення здійснюємо засобом виконання практичних вправ:

1. Покладіть на парту 5 жовтих квадратів. Покладіть під ними стільки ж червоних квадратів. Скільки треба покласти червоних квадратів? Покладіть поряд ще один червоний квадрат. Тепер квадратів стільки ж? (Ні. Червоних квадратів більше). На скільки червоних квадратів більше, ніж жовтих? (На 1).

Розгляньте, як виконали схематичний малюнок. Яких квадратів більше? На скільки більше?

Червоних квадратів стільки ж, скільки й жовтих та ще 1. На 1 більше - це значить стільки ж та ще 1.

Якою арифметичною дією знайдемо 5 та ще 1? (Дією додавання.) Складемо рівність: 5 + 1=6. Червоних квадратів 6. Щоб дізнатися про число, яке на 1 більше, треба додати!

Аналогічно розглядаємо зменшення на 1.

Зміна значення суми в залежності від зміни одного з доданків. Зміна значення різниці в залежності від зміни зменшуваного. При вивченні таблиць додавання існує можливість познайомити учнів спочатку з характером зміни значення суми в залежності від зміни одного з доданків: доданок і значення сума змінюються в одному напрямку. Потім перейти до формулювання правила: якщо перший доданок збільшиться (зменшиться) на кілька одиниць, то значення суми так само збільшиться (зменшиться) на стільки ж одиниць. При вивченні таблиць віднімання можна спочатку познайомити учнів із характером зміни значення різниці залежно від зміни зменшуваного: зменшуване і значення різниці змінюються в одному напрямку. Далі відбувається ознайомлення з правилом: якщо зменшуване збільшиться (зменшиться) на кілька одиниць, то й значення різниці так само збільшиться (зменшиться) на стільки ж одиниць,

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Складання і засвоєння таблиць додавання і віднімання з переходом через десяток.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.