Методика навчання письмового додавання та віднімання двоцифрових чисел

При ознайомленні з письмовим додаванням та відніманням треба обґрунтувати необхідність введення нового прийому обчислення. Учням пропонується обчислити суму чисел 37 та 59 порозрядно:

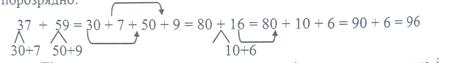
Діти впевнюються в тому, що так міркувати дуже довго і складно, тому вчитель показує новий прийом обчислення - письмовий і іншу форму запису - у стовпчик:

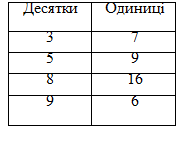Учні розглядають завдання на додавання стовпчиком у нумераційній таблиці. З’ясовують, як підписані числа. Дізнаються, чому не можна залишити 16 одиниць у розряді одиниць: 16 у =1д.6од. Розглядають, як записано результат.

Зазначаємо, що починати додавання з розряду десятків не можна, тому що, можливо, що ще один десяток перейде від одиниць; отже, додавання розпочинають з розряду одиниць.

Таким чином, дістаємо висновку: двоцифрові числа можна додавати стовпчиком. Доданки записують так: одиниці під одиницями, десятки під десятками. Додавання починають з розряду одиниць, при цьому пам'ятаючи, що 10 одиниць складають 1 десяток, потім додають десятки. Наприклад:

Записуємо числа стовпчиком: одиниці під одиницями, десятки під десятками. Додавання починаємо з розряду одиниць: 5 одиниць плюс 8 одиниць, отримаємо 13 од.

13 одиниць - це 1 десяток і 3 одиниці; 3 одиниці пишемо під одиницями, а 1 десяток переходить до десятків; стрілочкою показуємо, що один десяток перейшов до десятків, і, додаючи десятки, його слід врахувати. Додаємо десятки: 6 десятків плюс 2 десятки, отримаємо 8 десятків, та ще 1 десяток перейшов, буде 9 десятків; пишемо 9 під десятками.

Після введення письмового додавання двоцифрових чисел знайомимо учнів з письмовим відніманням. Перед ними ставиться проблемне запитання: „Чи можна так само виконувати віднімання - стовпчиком?”. Спочатку можна розглянути випадок віднімання без переходу через розряд. Тут учні переносять спосіб запису чисел стовпчиком і порядок міркування: спочатку віднімають одиниці, а потім - десятки:

Але наступний випадок створює проблемну ситуацію:

Записавши числа стовпчиком одиниці під одиницями, десятки під десятками, учні пробують відняти одиниці, але з 6 одиниць не можна відняти 8 одиниць. Тому позичаємо 1 десяток у десятків (показавши це стрілочкою), і роздроблюємо його в одиниці. 1 десяток - це 10 одиниць, і ще є 6 одиниць, всього 16 одиниць. Від 16-ти одиниць віднімаємо 8, маємо 8 одиниць, підписуємо результат під одиницями. Переходимо до десятків: було 3 десятки, позичили 1 десяток, лишилося 2 десятки; 2 десятки мінус 1 десяток, отримаємо 1 десяток; результат запишемо під десятками.

При вивченні письмового додавання і віднімання розглядаються випадки без переходу через розряд, випадки з переходом через розряд, а також випадки додавання, коли сума одиниць дорівнює 10, і віднімання, коли треба із 0 одиниць відняти кілька одиниць:

<== попередня сторінка	\|	наступна сторінка ==>
Спосіб округлення	\|	Додавання та віднімання двоцифрових чисел

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.