• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лінійна залежність векторів

Означення 3.3.1.Лінійна комбінація векторів називається нульовою, якщо вона дорівнює нульовому вектору: .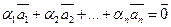

Означення 3.3.2.Лінійна комбінація векторів називається тривіальною, якщо усі коефіцієнти у ній дорівнюють нулю:

.

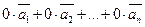Зрозуміло, що кожна тривіальна комбінація – нульова. Але не кожна нульова комбінація – тривіальна.

Приклад.Розглянемо таку лінійну комбінацію векторів 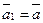та ( ):

.

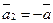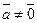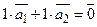Згідно з означеннями 3.3.1 та 3.3.2 вона не тривіальна, але нульова.

Означення 3.3.3.Вектори 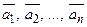називають лінійно залежними, якщо існує нетривіальна нульова комбінація цих векторів. Іншими словами, якщо існують такі числа 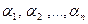, серед яких хоча б одне відмінно від нуля, що .

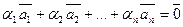Означення 3.3.4.Вектори 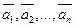називають лінійно незалежними, якщо рівність 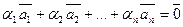можлива тільки при 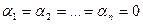, тобто нульова лінійна комбінація векторів 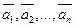може бути тільки тривіальною.

Приклад. Довести, що система, яка складається з одного ненульового вектору – лінійно незалежна.

Розв’язання. Нехай 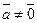. Побудуємо лінійну комбінацію, яка дорівнює нулю: 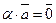. Оскільки 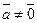, то 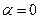. Тобто нульова комбінація 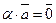існує тільки в одному випадку, коли ця комбінація тривіальна, внаслідок чого система з одного ненульового вектора лінійно незалежна.

З аналогічних міркувань легко показати, що навпаки, система, яка складається з одного нульового вектора – лінійно залежна.

Приклад. Нехай система векторів 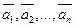містить нульовий вектор. З'ясувати, чи є вектори лінійно залежними або лінійно незалежними.

Розв’язання. Припустимо, що 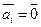і побудуємо таку нульову лінійну комбінацію цих векторів:

.

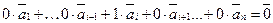У цій лінійній комбінації векторів коефіцієнт при i-му векторі відмінний від нуля. Отже, знайдена нетривіальна нульова комбінація зазначених векторів, таким чином розглянуті вектори лінійно залежні.

Фактично міркування останнього прикладу доводять таку лему.

Лема 3.3.1. Система лінійно незалежних векторів не може містити нульовий вектор.

Умовимося вектор 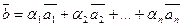називати лінійною комбінацією векторів 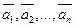. У цій рівності 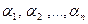– дійсні числа.

Теорема 3.3.1. Для того, щоб система векторів була лінійно залежною, необхідно й достатньо, щоб один з векторів (але не кожний!) був лінійною комбінацією інших векторів системи.

4 Þ: Нехай вектори 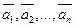– лінійно залежні, покажемо, що один з них є лінійною комбінацією інших. Дійсно, якщо вектори 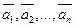– лінійно залежні, то існує такий набір чисел 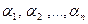серед яких є відмінні від нуля, що 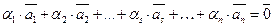. Нехай 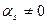, тоді, вектор 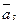можна подати у вигляді

.

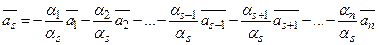Отже, вектор 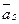є лінійною комбінацією інших векторів.

Доведемо важливе для подальшого твердження: якщо один з векторів 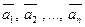є лінійною комбінацією інших, то ці вектори лінійно залежні. Дійсно, без обмеження загальності міркувань можна вважати, що, наприклад, вектор 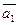є лінійною комбінацією інших векторів. Тоді 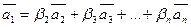. Додамо до обох частин цієї рівності вектор 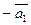, одержимо 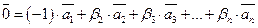. В отриманій рівності коефіцієнт при 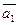не дорівнює нулю, звідки згідно з означенням 3.3.3 виходить, що вектори 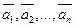– лінійно залежні. 3

Теорема 3.3.2. Два вектори лінійно залежні тоді й тільки тоді, коли вони колінеарні.

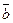4 Дійсно, якщо два вектори та лінійно залежні, то існують такі числа 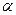і 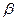, з яких хоча б одне не дорівнює нулю, що 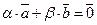. Нехай 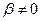тоді 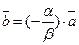. Остання рівність означає, що напрямки векторів та 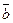або збігаються, або протилежні (якщо вони ненульові). Якщо вони нульові, то вони колінеарні за згодою (див. § 3.1). В усіх випадках лінійно залежні вектори і 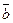– колінеарні.

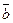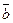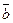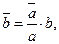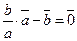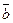Покажемо, що колінеарні вектори і – лінійно залежні. Якщо один з векторів або є нульовим твердження очевидне (див. приклад вище).Тому нехай і –ненульові вектори. Якщо їх напрямки збігаються, то тобто , а це означає, що та – лінійно залежні. Якщо ж напрямки векторів і 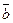протилежні, то 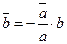. І в цьому випадку та 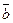також лінійно залежні. 3

Наслідок. Два неколінеарні вектори лінійно незалежні.

Теорема 3.3.3 [2]. Три вектори лінійно залежні тоді й тільки тоді, коли вони компланарні.

Наслідок. Якщо три вектори некомпланарні, то вони, лінійно незалежні.

Теорема 3.3.4[2]. Усякі чотири геометричні вектори лінійно залежні.

Переглядів: 6715